Provable In-context Learning for Mixture of Linear Regressions using Transformers

We theoretically investigate the in-context learning capabilities of transformers in the context of learning mixtures of linear regression models. For the case of two mixtures, we demonstrate the existence of transformers that can achieve an accuracy, relative to the oracle predictor, of order $\mathcal{\tilde{O}}((d/n)^{1/4})$ in the low signal-to-noise ratio (SNR) regime and $\mathcal{\tilde{O}}(\sqrt{d/n})$ in the high SNR regime, where $n$ is the length of the prompt, and $d$ is the dimension of the problem. Additionally, we derive in-context excess risk bounds of order $\mathcal{O}(L/\sqrt{B})$, where $B$ denotes the number of (training) prompts, and $L$ represents the number of attention layers. The order of $L$ depends on whether the SNR is low or high. In the high SNR regime, we extend the results to $K$-component mixture models for finite $K$. Extensive simulations also highlight the advantages of transformers for this task, outperforming other baselines such as the Expectation-Maximization algorithm.

Meta-Learning with Generalized Ridge Regression: High-dimensional Asymptotics, Optimality and Hyper-covariance Estimation

Meta-learning involves training models on a variety of training tasks in a way that enables them to generalize well on new, unseen test tasks. In this work, we consider meta-learning within the framework of high-dimensional multivariate random-effects linear models and study generalized ridge-regression based predictions. The statistical intuition of using generalized ridge regression in this setting is that the covariance structure of the random regression coefficients could be leveraged to make better predictions on new tasks. Accordingly, we first characterize the precise asymptotic behavior of the predictive risk for a new test task when the data dimension grows proportionally to the number of samples per task. We next show that this predictive risk is optimal when the weight matrix in generalized ridge regression is chosen to be the inverse of the covariance matrix of random coefficients. Finally, we propose and analyze an estimator of the inverse covariance matrix of random regression coefficients based on data from the training tasks. As opposed to intractable MLE-type estimators, the proposed estimators could be computed efficiently as they could be obtained by solving (global) geodesically-convex optimization problems. Our analysis and methodology use tools from random matrix theory and Riemannian optimization. Simulation results demonstrate the improved generalization performance of the proposed method on new unseen test tasks within the considered framework.

Statistical Inference for Polyak-Ruppert Averaged Zeroth-order Stochastic Gradient Algorithm

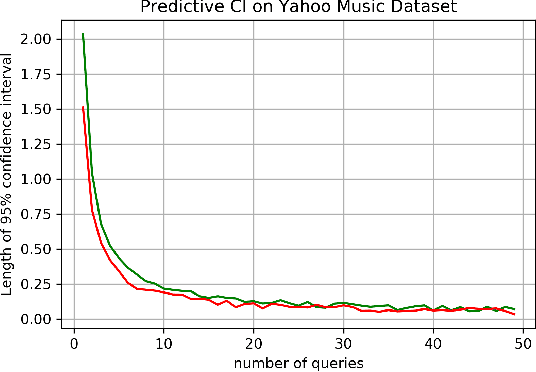
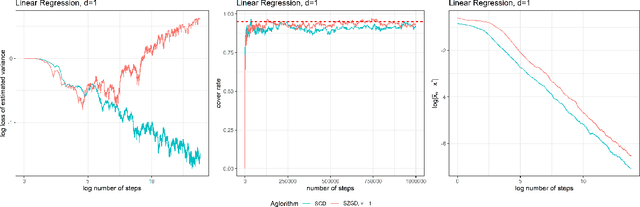
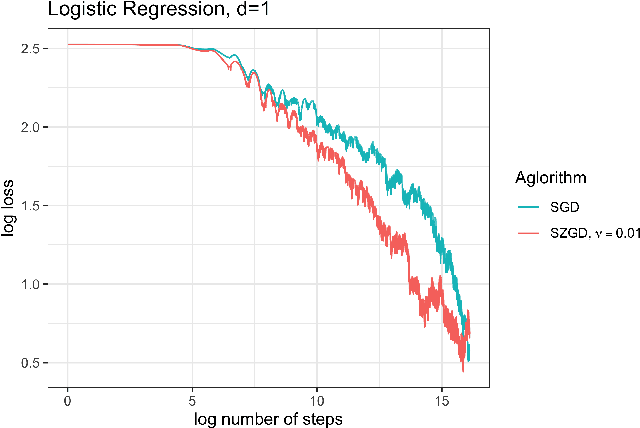
As machine learning models are deployed in critical applications, it becomes important to not just provide point estimators of the model parameters (or subsequent predictions), but also quantify the uncertainty associated with estimating the model parameters via confidence sets. In the last decade, estimating or training in several machine learning models has become synonymous with running stochastic gradient algorithms. However, computing the stochastic gradients in several settings is highly expensive or even impossible at times. An important question which has thus far not been addressed sufficiently in the statistical machine learning literature is that of equipping zeroth-order stochastic gradient algorithms with practical yet rigorous inferential capabilities. Towards this, in this work, we first establish a central limit theorem for Polyak-Ruppert averaged stochastic gradient algorithm in the zeroth-order setting. We then provide online estimators of the asymptotic covariance matrix appearing in the central limit theorem, thereby providing a practical procedure for constructing asymptotically valid confidence sets (or intervals) for parameter estimation (or prediction) in the zeroth-order setting.