Meta-Learning with Generalized Ridge Regression: High-dimensional Asymptotics, Optimality and Hyper-covariance Estimation

Meta-learning involves training models on a variety of training tasks in a way that enables them to generalize well on new, unseen test tasks. In this work, we consider meta-learning within the framework of high-dimensional multivariate random-effects linear models and study generalized ridge-regression based predictions. The statistical intuition of using generalized ridge regression in this setting is that the covariance structure of the random regression coefficients could be leveraged to make better predictions on new tasks. Accordingly, we first characterize the precise asymptotic behavior of the predictive risk for a new test task when the data dimension grows proportionally to the number of samples per task. We next show that this predictive risk is optimal when the weight matrix in generalized ridge regression is chosen to be the inverse of the covariance matrix of random coefficients. Finally, we propose and analyze an estimator of the inverse covariance matrix of random regression coefficients based on data from the training tasks. As opposed to intractable MLE-type estimators, the proposed estimators could be computed efficiently as they could be obtained by solving (global) geodesically-convex optimization problems. Our analysis and methodology use tools from random matrix theory and Riemannian optimization. Simulation results demonstrate the improved generalization performance of the proposed method on new unseen test tasks within the considered framework.

Sparse Equisigned PCA: Algorithms and Performance Bounds in the Noisy Rank-1 Setting

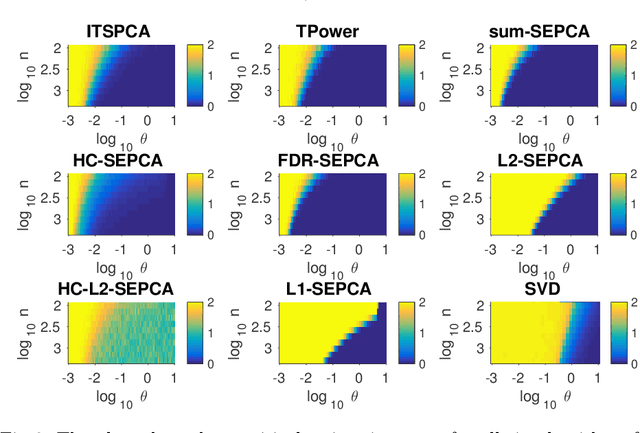
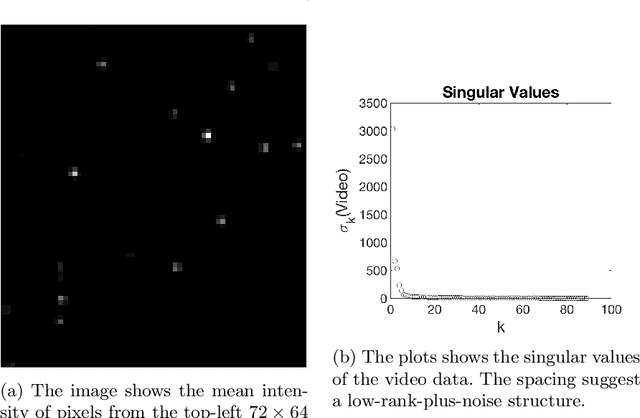
Singular value decomposition (SVD) based principal component analysis (PCA) breaks down in the high-dimensional and limited sample size regime below a certain critical eigen-SNR that depends on the dimensionality of the system and the number of samples. Below this critical eigen-SNR, the estimates returned by the SVD are asymptotically uncorrelated with the latent principal components. We consider a setting where the left singular vector of the underlying rank one signal matrix is assumed to be sparse and the right singular vector is assumed to be equisigned, that is, having either only nonnegative or only nonpositive entries. We consider six different algorithms for estimating the sparse principal component based on different statistical criteria and prove that by exploiting sparsity, we recover consistent estimates in the low eigen-SNR regime where the SVD fails. Our analysis reveals conditions under which a coordinate selection scheme based on a \textit{sum-type decision statistic} outperforms schemes that utilize the $\ell_1$ and $\ell_2$ norm-based statistics. We derive lower bounds on the size of detectable coordinates of the principal left singular vector and utilize these lower bounds to derive lower bounds on the worst-case risk. Finally, we verify our findings with numerical simulations and illustrate the performance with a video data example, where the interest is in identifying objects.