Sparse Equisigned PCA: Algorithms and Performance Bounds in the Noisy Rank-1 Setting

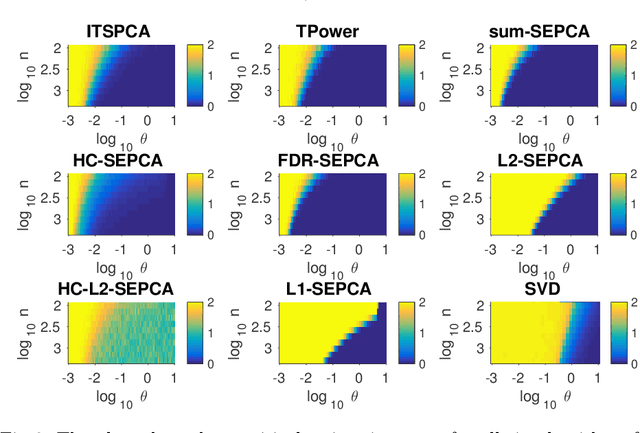
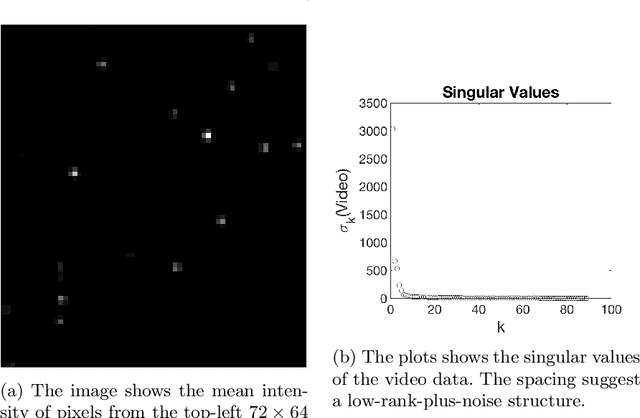
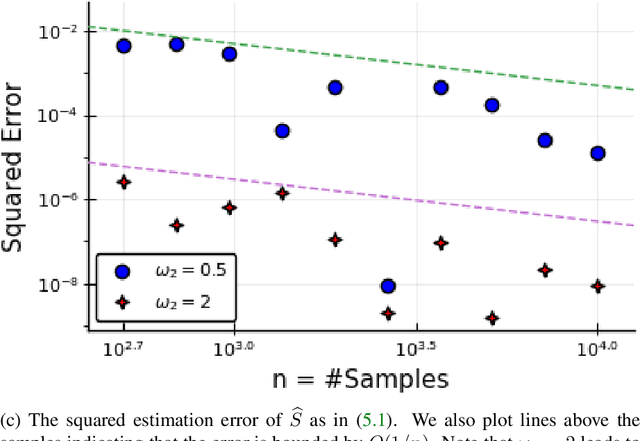
Singular value decomposition (SVD) based principal component analysis (PCA) breaks down in the high-dimensional and limited sample size regime below a certain critical eigen-SNR that depends on the dimensionality of the system and the number of samples. Below this critical eigen-SNR, the estimates returned by the SVD are asymptotically uncorrelated with the latent principal components. We consider a setting where the left singular vector of the underlying rank one signal matrix is assumed to be sparse and the right singular vector is assumed to be equisigned, that is, having either only nonnegative or only nonpositive entries. We consider six different algorithms for estimating the sparse principal component based on different statistical criteria and prove that by exploiting sparsity, we recover consistent estimates in the low eigen-SNR regime where the SVD fails. Our analysis reveals conditions under which a coordinate selection scheme based on a \textit{sum-type decision statistic} outperforms schemes that utilize the $\ell_1$ and $\ell_2$ norm-based statistics. We derive lower bounds on the size of detectable coordinates of the principal left singular vector and utilize these lower bounds to derive lower bounds on the worst-case risk. Finally, we verify our findings with numerical simulations and illustrate the performance with a video data example, where the interest is in identifying objects.

Free Component Analysis: Theory, Algorithms & Applications

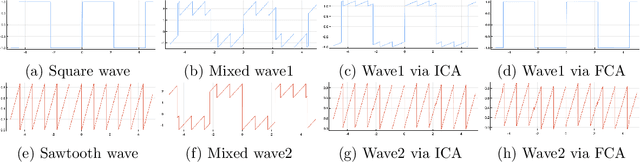
We describe a method for unmixing mixtures of freely independent random variables in a manner analogous to the independent component analysis (ICA) based method for unmixing independent random variables from their additive mixtures. Random matrices play the role of free random variables in this context so the method we develop, which we call Free component analysis (FCA), unmixes matrices from additive mixtures of matrices. We describe the theory, the various algorithms, and compare FCA to ICA. We show that FCA performs comparably to, and often better than, ICA in every application, such as image and speech unmixing, where ICA has been known to succeed. Our computational experiments suggest that not-so-random matrices, such as images and spectrograms of waveforms are (closer to being) freer "in the wild" than we might have theoretically expected.

Time Series Source Separation using Dynamic Mode Decomposition

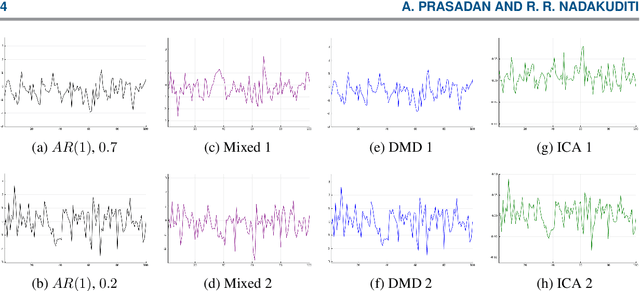
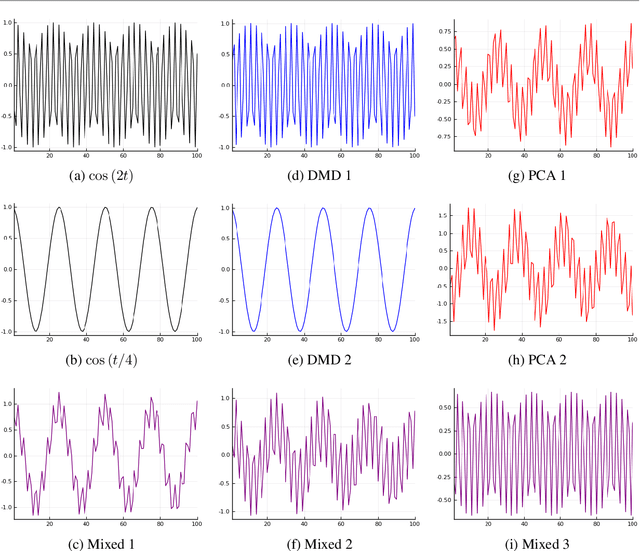
The dynamic mode decomposition (DMD) extracted dynamic modes are the non-orthogonal eigenvectors of the matrix that best approximates the one-step temporal evolution of the multivariate samples. In the context of dynamic system analysis, the extracted dynamic modes are a generalization of global stability modes. We apply DMD to a data matrix whose rows are linearly independent, additive mixtures of latent time series. We show that when the latent time series are uncorrelated at a lag of one time-step then, in the large sample limit, the recovered dynamic modes will approximate, up to a column-wise normalization, the columns of the mixing matrix. Thus, DMD is a time series blind source separation algorithm in disguise, but is different from closely related second order algorithms such as SOBI and AMUSE. All can unmix mixed ergodic Gaussian time series in a way that ICA fundamentally cannot. We use our insights on single lag DMD to develop a higher-lag extension, analyze the finite sample performance with and without randomly missing data, and identify settings where the higher lag variant can outperform the conventional single lag variant. We validate our results with numerical simulations, and highlight how DMD can be used in change point detection.

Online Adaptive Image Reconstruction (OnAIR) Using Dictionary Models

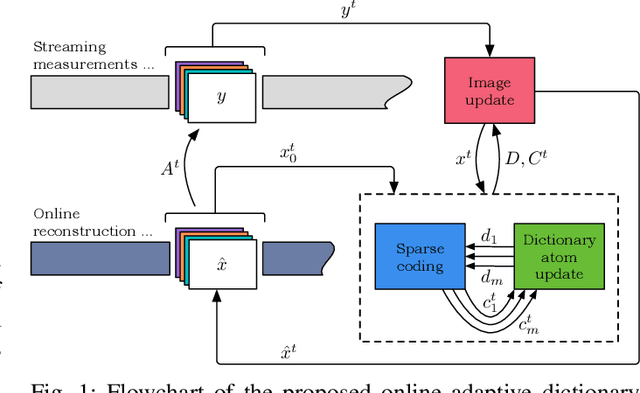
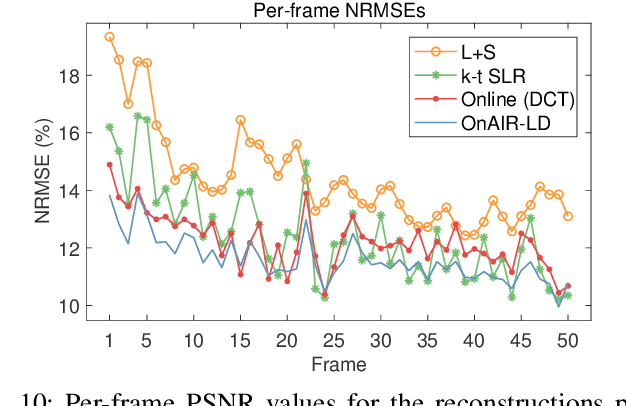
Sparsity and low-rank models have been popular for reconstructing images and videos from limited or corrupted measurements. Dictionary or transform learning methods are useful in applications such as denoising, inpainting, and medical image reconstruction. This paper proposes a framework for online (or time-sequential) adaptive reconstruction of dynamic image sequences from linear (typically undersampled) measurements. We model the spatiotemporal patches of the underlying dynamic image sequence as sparse in a dictionary, and we simultaneously estimate the dictionary and the images sequentially from streaming measurements. Multiple constraints on the adapted dictionary are also considered such as a unitary matrix, or low-rank dictionary atoms that provide additional efficiency or robustness. The proposed online algorithms are memory efficient and involve simple updates of the dictionary atoms, sparse coefficients, and images. Numerical experiments demonstrate the usefulness of the proposed methods in inverse problems such as video reconstruction or inpainting from noisy, subsampled pixels, and dynamic magnetic resonance image reconstruction from very limited measurements.

Robust Photometric Stereo via Dictionary Learning

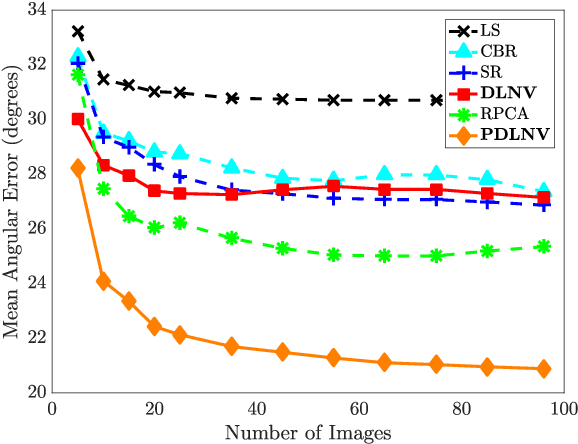
Photometric stereo is a method that seeks to reconstruct the normal vectors of an object from a set of images of the object illuminated under different light sources. While effective in some situations, classical photometric stereo relies on a diffuse surface model that cannot handle objects with complex reflectance patterns, and it is sensitive to non-idealities in the images. In this work, we propose a novel approach to photometric stereo that relies on dictionary learning to produce robust normal vector reconstructions. Specifically, we develop two formulations for applying dictionary learning to photometric stereo. We propose a model that applies dictionary learning to regularize and reconstruct the normal vectors from the images under the classic Lambertian reflectance model. We then generalize this model to explicitly model non-Lambertian objects. We investigate both approaches through extensive experimentation on synthetic and real benchmark datasets and observe state-of-the-art performance compared to existing robust photometric stereo methods.

Panoramic Robust PCA for Foreground-Background Separation on Noisy, Free-Motion Camera Video

This work presents a novel approach for robust PCA with total variation regularization for foreground-background separation and denoising on noisy, moving camera video. Our proposed algorithm registers the raw (possibly corrupted) frames of a video and then jointly processes the registered frames to produce a decomposition of the scene into a low-rank background component that captures the static components of the scene, a smooth foreground component that captures the dynamic components of the scene, and a sparse component that isolates corruptions. Unlike existing methods, our proposed algorithm produces a panoramic low-rank component that spans the entire field of view, automatically stitching together corrupted data from partially overlapping scenes. The low-rank portion of our robust PCA model is based on a recently discovered optimal low-rank matrix estimator (OptShrink) that requires no parameter tuning. We demonstrate the performance of our algorithm on both static and moving camera videos corrupted by noise and outliers.

Robust Surface Reconstruction from Gradients via Adaptive Dictionary Regularization

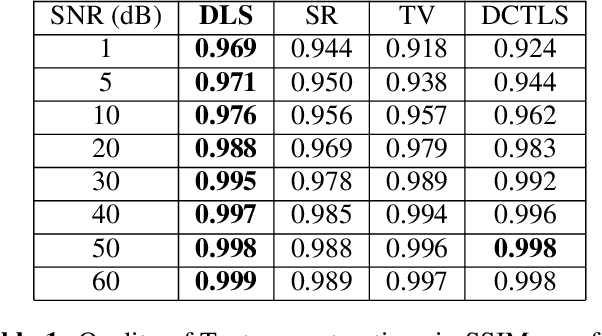
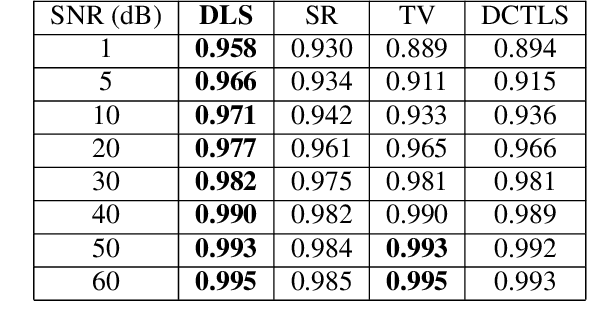
This paper introduces a novel approach to robust surface reconstruction from photometric stereo normal vector maps that is particularly well-suited for reconstructing surfaces from noisy gradients. Specifically, we propose an adaptive dictionary learning based approach that attempts to simultaneously integrate the gradient fields while sparsely representing the spatial patches of the reconstructed surface in an adaptive dictionary domain. We show that our formulation learns the underlying structure of the surface, effectively acting as an adaptive regularizer that enforces a smoothness constraint on the reconstructed surface. Our method is general and may be coupled with many existing approaches in the literature to improve the integrity of the reconstructed surfaces. We demonstrate the performance of our method on synthetic data as well as real photometric stereo data and evaluate its robustness to noise.

Robust Photometric Stereo Using Learned Image and Gradient Dictionaries

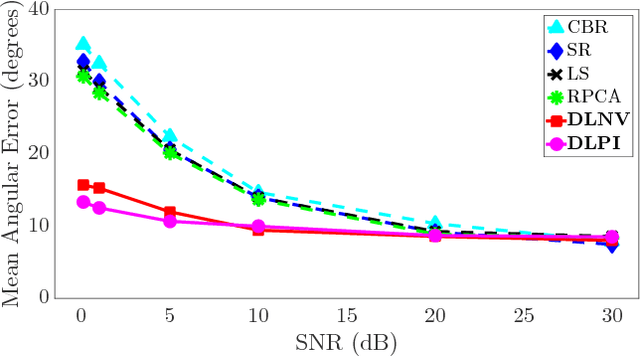
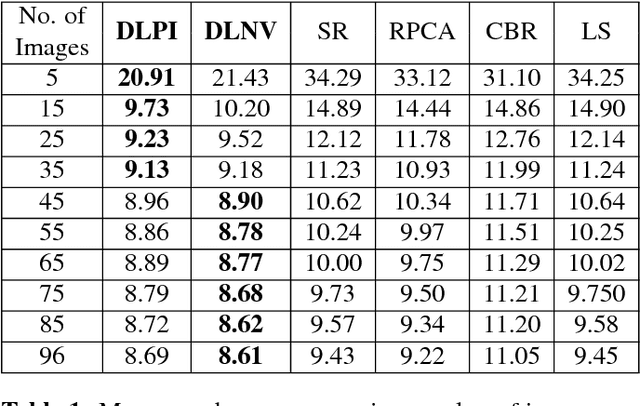
Photometric stereo is a method for estimating the normal vectors of an object from images of the object under varying lighting conditions. Motivated by several recent works that extend photometric stereo to more general objects and lighting conditions, we study a new robust approach to photometric stereo that utilizes dictionary learning. Specifically, we propose and analyze two approaches to adaptive dictionary regularization for the photometric stereo problem. First, we propose an image preprocessing step that utilizes an adaptive dictionary learning model to remove noise and other non-idealities from the image dataset before estimating the normal vectors. We also propose an alternative model where we directly apply the adaptive dictionary regularization to the normal vectors themselves during estimation. We study the practical performance of both methods through extensive simulations, which demonstrate the state-of-the-art performance of both methods in the presence of noise.

Augmented Robust PCA For Foreground-Background Separation on Noisy, Moving Camera Video

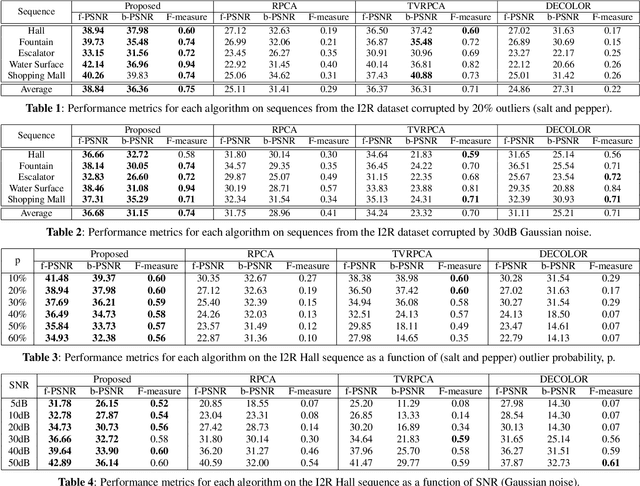
This work presents a novel approach for robust PCA with total variation regularization for foreground-background separation and denoising on noisy, moving camera video. Our proposed algorithm registers the raw (possibly corrupted) frames of a video and then jointly processes the registered frames to produce a decomposition of the scene into a low-rank background component that captures the static components of the scene, a smooth foreground component that captures the dynamic components of the scene, and a sparse component that can isolate corruptions and other non-idealities. Unlike existing methods, our proposed algorithm produces a panoramic low-rank component that spans the entire field of view, automatically stitching together corrupted data from partially overlapping scenes. The low-rank portion of our robust PCA model is based on a recently discovered optimal low-rank matrix estimator (OptShrink) that requires no parameter tuning. We demonstrate the performance of our algorithm on both static and moving camera videos corrupted by noise and outliers.

Efficient Sum of Outer Products Dictionary Learning (SOUP-DIL) - The $\ell_0$ Method

The sparsity of natural signals and images in a transform domain or dictionary has been extensively exploited in several applications such as compression, denoising and inverse problems. More recently, data-driven adaptation of synthesis dictionaries has shown promise in many applications compared to fixed or analytical dictionary models. However, dictionary learning problems are typically non-convex and NP-hard, and the usual alternating minimization approaches for these problems are often computationally expensive, with the computations dominated by the NP-hard synthesis sparse coding step. In this work, we investigate an efficient method for $\ell_{0}$ "norm"-based dictionary learning by first approximating the training data set with a sum of sparse rank-one matrices and then using a block coordinate descent approach to estimate the unknowns. The proposed block coordinate descent algorithm involves efficient closed-form solutions. In particular, the sparse coding step involves a simple form of thresholding. We provide a convergence analysis for the proposed block coordinate descent approach. Our numerical experiments show the promising performance and significant speed-ups provided by our method over the classical K-SVD scheme in sparse signal representation and image denoising.