Time Series Source Separation using Dynamic Mode Decomposition

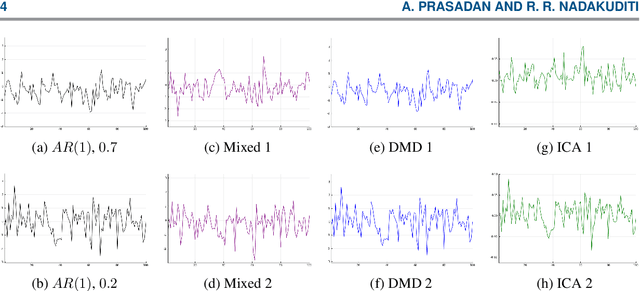
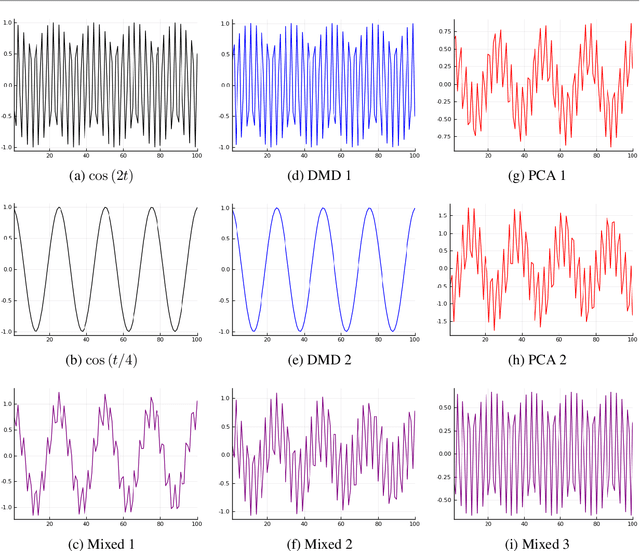
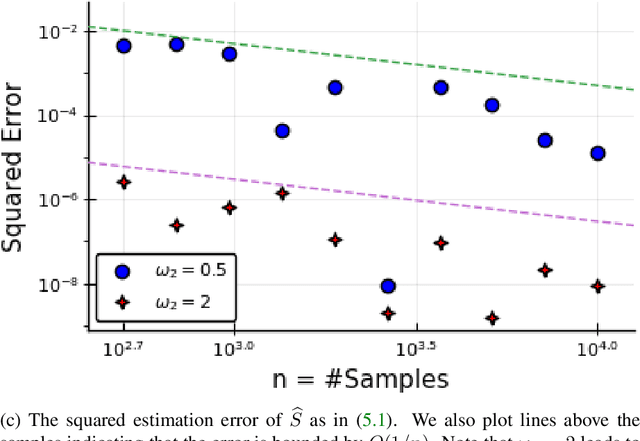
The dynamic mode decomposition (DMD) extracted dynamic modes are the non-orthogonal eigenvectors of the matrix that best approximates the one-step temporal evolution of the multivariate samples. In the context of dynamic system analysis, the extracted dynamic modes are a generalization of global stability modes. We apply DMD to a data matrix whose rows are linearly independent, additive mixtures of latent time series. We show that when the latent time series are uncorrelated at a lag of one time-step then, in the large sample limit, the recovered dynamic modes will approximate, up to a column-wise normalization, the columns of the mixing matrix. Thus, DMD is a time series blind source separation algorithm in disguise, but is different from closely related second order algorithms such as SOBI and AMUSE. All can unmix mixed ergodic Gaussian time series in a way that ICA fundamentally cannot. We use our insights on single lag DMD to develop a higher-lag extension, analyze the finite sample performance with and without randomly missing data, and identify settings where the higher lag variant can outperform the conventional single lag variant. We validate our results with numerical simulations, and highlight how DMD can be used in change point detection.