Free Component Analysis: Theory, Algorithms & Applications

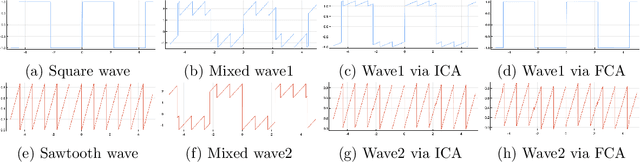
We describe a method for unmixing mixtures of freely independent random variables in a manner analogous to the independent component analysis (ICA) based method for unmixing independent random variables from their additive mixtures. Random matrices play the role of free random variables in this context so the method we develop, which we call Free component analysis (FCA), unmixes matrices from additive mixtures of matrices. We describe the theory, the various algorithms, and compare FCA to ICA. We show that FCA performs comparably to, and often better than, ICA in every application, such as image and speech unmixing, where ICA has been known to succeed. Our computational experiments suggest that not-so-random matrices, such as images and spectrograms of waveforms are (closer to being) freer "in the wild" than we might have theoretically expected.