ALPCAH: Subspace Learning for Sample-wise Heteroscedastic Data

Principal component analysis (PCA) is a key tool in the field of data dimensionality reduction. However, some applications involve heterogeneous data that vary in quality due to noise characteristics associated with each data sample. Heteroscedastic methods aim to deal with such mixed data quality. This paper develops a subspace learning method, named ALPCAH, that can estimate the sample-wise noise variances and use this information to improve the estimate of the subspace basis associated with the low-rank structure of the data. Our method makes no distributional assumptions of the low-rank component and does not assume that the noise variances are known. Further, this method uses a soft rank constraint that does not require subspace dimension to be known. Additionally, this paper develops a matrix factorized version of ALPCAH, named LR-ALPCAH, that is much faster and more memory efficient at the cost of requiring subspace dimension to be known or estimated. Simulations and real data experiments show the effectiveness of accounting for data heteroscedasticity compared to existing algorithms. Code available at https://github.com/javiersc1/ALPCAH.

Smooth optimization algorithms for global and locally low-rank regularizers

Many inverse problems and signal processing problems involve low-rank regularizers based on the nuclear norm. Commonly, proximal gradient methods (PGM) are adopted to solve this type of non-smooth problems as they can offer fast and guaranteed convergence. However, PGM methods cannot be simply applied in settings where low-rank models are imposed locally on overlapping patches; therefore, heuristic approaches have been proposed that lack convergence guarantees. In this work we propose to replace the nuclear norm with a smooth approximation in which a Huber-type function is applied to each singular value. By providing a theoretical framework based on singular value function theory, we show that important properties can be established for the proposed regularizer, such as: convexity, differentiability, and Lipschitz continuity of the gradient. Moreover, we provide a closed-form expression for the regularizer gradient, enabling the use of standard iterative gradient-based optimization algorithms (e.g., nonlinear conjugate gradient) that can easily address the case of overlapping patches and have well-known convergence guarantees. In addition, we provide a novel step-size selection strategy based on a quadratic majorizer of the line-search function that leverages the Huber characteristics of the proposed regularizer. Finally, we assess the proposed optimization framework by providing empirical results in dynamic magnetic resonance imaging (MRI) reconstruction in the context of locally low-rank models with overlapping patches.

Convergent Complex Quasi-Newton Proximal Methods for Gradient-Driven Denoisers in Compressed Sensing MRI Reconstruction

In compressed sensing (CS) MRI, model-based methods are pivotal to achieving accurate reconstruction. One of the main challenges in model-based methods is finding an effective prior to describe the statistical distribution of the target image. Plug-and-Play (PnP) and REgularization by Denoising (RED) are two general frameworks that use denoisers as the prior. While PnP/RED methods with convolutional neural networks (CNNs) based denoisers outperform classical hand-crafted priors in CS MRI, their convergence theory relies on assumptions that do not hold for practical CNNs. The recently developed gradient-driven denoisers offer a framework that bridges the gap between practical performance and theoretical guarantees. However, the numerical solvers for the associated minimization problem remain slow for CS MRI reconstruction. This paper proposes a complex quasi-Newton proximal method that achieves faster convergence than existing approaches. To address the complex domain in CS MRI, we propose a modified Hessian estimation method that guarantees Hermitian positive definiteness. Furthermore, we provide a rigorous convergence analysis of the proposed method for nonconvex settings. Numerical experiments on both Cartesian and non-Cartesian sampling trajectories demonstrate the effectiveness and efficiency of our approach.

Bilevel Optimized Implicit Neural Representation for Scan-Specific Accelerated MRI Reconstruction

Deep Learning (DL) methods can reconstruct highly accelerated magnetic resonance imaging (MRI) scans, but they rely on application-specific large training datasets and often generalize poorly to out-of-distribution data. Self-supervised deep learning algorithms perform scan-specific reconstructions, but still require complicated hyperparameter tuning based on the acquisition and often offer limited acceleration. This work develops a bilevel-optimized implicit neural representation (INR) approach for scan-specific MRI reconstruction. The method automatically optimizes the hyperparameters for a given acquisition protocol, enabling a tailored reconstruction without training data. The proposed algorithm uses Gaussian process regression to optimize INR hyperparameters, accommodating various acquisitions. The INR includes a trainable positional encoder for high-dimensional feature embedding and a small multilayer perceptron for decoding. The bilevel optimization is computationally efficient, requiring only a few minutes per typical 2D Cartesian scan. On scanner hardware, the subsequent scan-specific reconstruction-using offline-optimized hyperparameters-is completed within seconds and achieves improved image quality compared to previous model-based and self-supervised learning methods.

On Adapting Randomized Nyström Preconditioners to Accelerate Variational Image Reconstruction

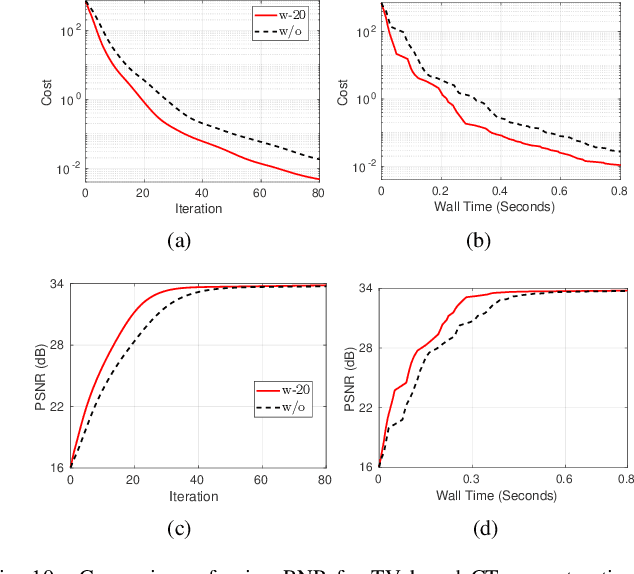
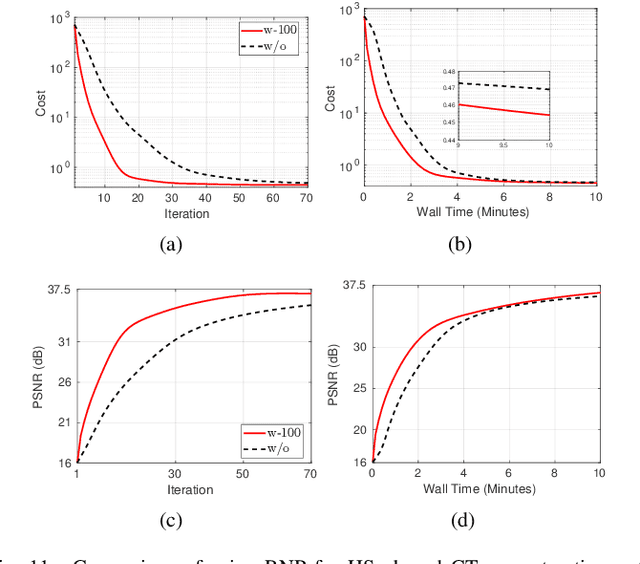
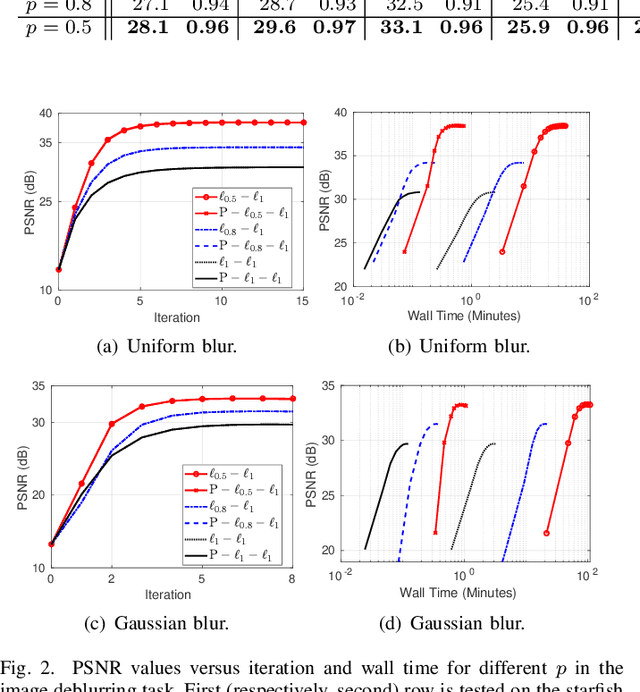
Model-based iterative reconstruction plays a key role in solving inverse problems. However, the associated minimization problems are generally large-scale, ill-posed, nonsmooth, and sometimes even nonconvex, which present challenges in designing efficient iterative solvers and often prevent their practical use. Preconditioning methods can significantly accelerate the convergence of iterative methods. In some applications, computing preconditioners on-the-fly is beneficial. Moreover, forward models in image reconstruction are typically represented as operators, and the corresponding explicit matrices are often unavailable, which brings additional challenges in designing preconditioners. Therefore, for practical use, computing and applying preconditioners should be computationally inexpensive. This paper adapts the randomized Nystr\"{o}m approximation to compute effective preconditioners that accelerate image reconstruction without requiring an explicit matrix for the forward model. We leverage modern GPU computational platforms to compute the preconditioner on-the-fly. Moreover, we propose efficient approaches for applying the preconditioner to problems with nonsmooth regularizers. Our numerical results on image deblurring, super-resolution with impulsive noise, and computed tomography reconstruction demonstrate the efficiency and effectiveness of the proposed preconditioner.

Patch-Based Diffusion Models Beat Whole-Image Models for Mismatched Distribution Inverse Problems

Diffusion models have achieved excellent success in solving inverse problems due to their ability to learn strong image priors, but existing approaches require a large training dataset of images that should come from the same distribution as the test dataset. When the training and test distributions are mismatched, artifacts and hallucinations can occur in reconstructed images due to the incorrect priors. In this work, we systematically study out of distribution (OOD) problems where a known training distribution is first provided. We first study the setting where only a single measurement obtained from the unknown test distribution is available. Next we study the setting where a very small sample of data belonging to the test distribution is available, and our goal is still to reconstruct an image from a measurement that came from the test distribution. In both settings, we use a patch-based diffusion prior that learns the image distribution solely from patches. Furthermore, in the first setting, we include a self-supervised loss that helps the network output maintain consistency with the measurement. Extensive experiments show that in both settings, the patch-based method can obtain high quality image reconstructions that can outperform whole-image models and can compete with methods that have access to large in-distribution training datasets. Furthermore, we show how whole-image models are prone to memorization and overfitting, leading to artifacts in the reconstructions, while a patch-based model can resolve these issues.

Shorter SPECT Scans Using Self-supervised Coordinate Learning to Synthesize Skipped Projection Views

Purpose: This study addresses the challenge of extended SPECT imaging duration under low-count conditions, as encountered in Lu-177 SPECT imaging, by developing a self-supervised learning approach to synthesize skipped SPECT projection views, thus shortening scan times in clinical settings. Methods: We employed a self-supervised coordinate-based learning technique, adapting the neural radiance field (NeRF) concept in computer vision to synthesize under-sampled SPECT projection views. For each single scan, we used self-supervised coordinate learning to estimate skipped SPECT projection views. The method was tested with various down-sampling factors (DFs=2, 4, 8) on both Lu-177 phantom SPECT/CT measurements and clinical SPECT/CT datasets, from 11 patients undergoing Lu-177 DOTATATE and 6 patients undergoing Lu-177 PSMA-617 radiopharmaceutical therapy. Results: For SPECT reconstructions, our method outperformed the use of linearly interpolated projections and partial projection views in relative contrast-to-noise-ratios (RCNR) averaged across different downsampling factors: 1) DOTATATE: 83% vs. 65% vs. 67% for lesions and 86% vs. 70% vs. 67% for kidney, 2) PSMA: 76% vs. 69% vs. 68% for lesions and 75% vs. 55% vs. 66% for organs, including kidneys, lacrimal glands, parotid glands, and submandibular glands. Conclusion: The proposed method enables reduction in acquisition time (by factors of 2, 4, or 8) while maintaining quantitative accuracy in clinical SPECT protocols by allowing for the collection of fewer projections. Importantly, the self-supervised nature of this NeRF-based approach eliminates the need for extensive training data, instead learning from each patient's projection data alone. The reduction in acquisition time is particularly relevant for imaging under low-count conditions and for protocols that require multiple-bed positions such as whole-body imaging.

DiffusionBlend: Learning 3D Image Prior through Position-aware Diffusion Score Blending for 3D Computed Tomography Reconstruction

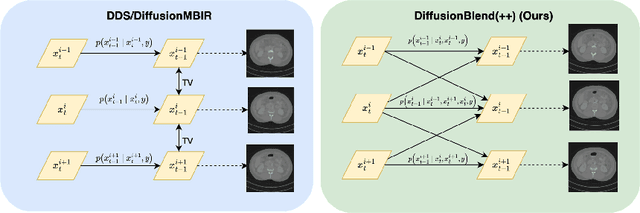
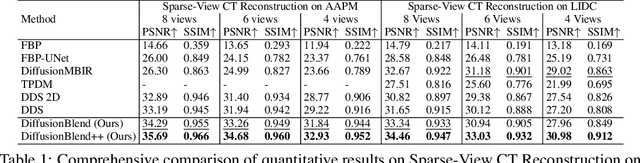
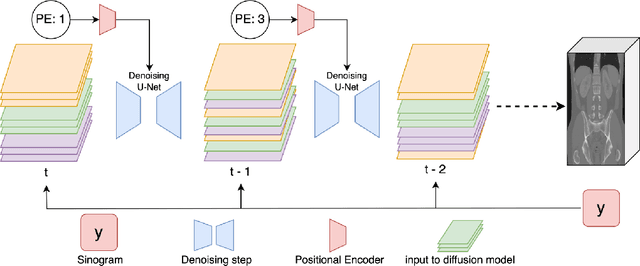
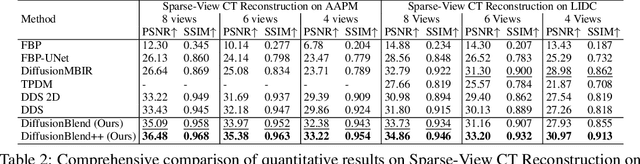
Diffusion models face significant challenges when employed for large-scale medical image reconstruction in real practice such as 3D Computed Tomography (CT). Due to the demanding memory, time, and data requirements, it is difficult to train a diffusion model directly on the entire volume of high-dimensional data to obtain an efficient 3D diffusion prior. Existing works utilizing diffusion priors on single 2D image slice with hand-crafted cross-slice regularization would sacrifice the z-axis consistency, which results in severe artifacts along the z-axis. In this work, we propose a novel framework that enables learning the 3D image prior through position-aware 3D-patch diffusion score blending for reconstructing large-scale 3D medical images. To the best of our knowledge, we are the first to utilize a 3D-patch diffusion prior for 3D medical image reconstruction. Extensive experiments on sparse view and limited angle CT reconstruction show that our DiffusionBlend method significantly outperforms previous methods and achieves state-of-the-art performance on real-world CT reconstruction problems with high-dimensional 3D image (i.e., $256 \times 256 \times 500$). Our algorithm also comes with better or comparable computational efficiency than previous state-of-the-art methods.

Learning Image Priors through Patch-based Diffusion Models for Solving Inverse Problems

Diffusion models can learn strong image priors from underlying data distribution and use them to solve inverse problems, but the training process is computationally expensive and requires lots of data. Such bottlenecks prevent most existing works from being feasible for high-dimensional and high-resolution data such as 3D images. This paper proposes a method to learn an efficient data prior for the entire image by training diffusion models only on patches of images. Specifically, we propose a patch-based position-aware diffusion inverse solver, called PaDIS, where we obtain the score function of the whole image through scores of patches and their positional encoding and utilize this as the prior for solving inverse problems. First of all, we show that this diffusion model achieves an improved memory efficiency and data efficiency while still maintaining the capability to generate entire images via positional encoding. Additionally, the proposed PaDIS model is highly flexible and can be plugged in with different diffusion inverse solvers (DIS). We demonstrate that the proposed PaDIS approach enables solving various inverse problems in both natural and medical image domains, including CT reconstruction, deblurring, and superresolution, given only patch-based priors. Notably, PaDIS outperforms previous DIS methods trained on entire image priors in the case of limited training data, demonstrating the data efficiency of our proposed approach by learning patch-based prior.

Provable Preconditioned Plug-and-Play Approach for Compressed Sensing MRI Reconstruction

Model-based methods play a key role in the reconstruction of compressed sensing (CS) MRI. Finding an effective prior to describe the statistical distribution of the image family of interest is crucial for model-based methods. Plug-and-play (PnP) is a general framework that uses denoising algorithms as the prior or regularizer. Recent work showed that PnP methods with denoisers based on pretrained convolutional neural networks outperform other classical regularizers in CS MRI reconstruction. However, the numerical solvers for PnP can be slow for CS MRI reconstruction. This paper proposes a preconditioned PnP (P^2nP) method to accelerate the convergence speed. Moreover, we provide proofs of the fixed-point convergence of the P^2nP iterates. Numerical experiments on CS MRI reconstruction with non-Cartesian sampling trajectories illustrate the effectiveness and efficiency of the P^2nP approach.