Transformers Provably Implement In-Context Reinforcement Learning with Policy Improvement

We investigate the ability of transformers to perform in-context reinforcement learning (ICRL), where a model must infer and execute learning algorithms from trajectory data without parameter updates. We show that a linear self-attention transformer block can provably implement policy-improvement methods, including semi-gradient SARSA and actor-critic, via explicit parameter constructions. Beyond existence, we design a teacher-mimicking training procedure, analyze its gradient-flow dynamics, and establish the first convergence guarantee in the ICRL literature: under suitable richness conditions on the training MDP distribution, gradient flow converges locally and exponentially to an optimal parameter manifold corresponding to the desired RL update. Empirically, training transformers on randomly generated tabular MDPs confirms these predictions: the learned models recover the parameter structure of our explicit constructions and, when deployed on unseen MDPs, deliver strong in-context control performance. Together, these results illuminate how transformer architectures internalize and execute classical reinforcement learning algorithms in context, bridging mechanistic understanding and training dynamics in ICRL.

Transformers Handle Endogeneity in In-Context Linear Regression

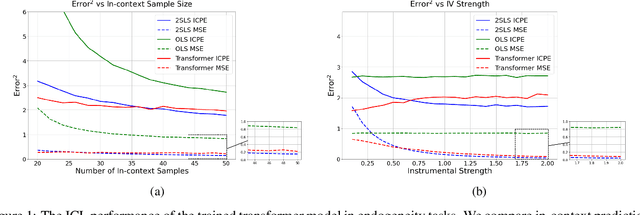
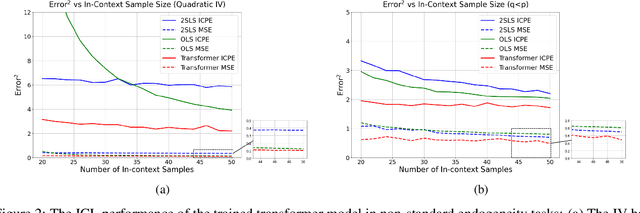
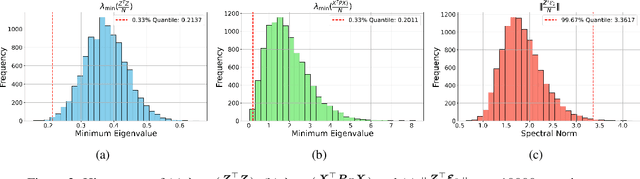
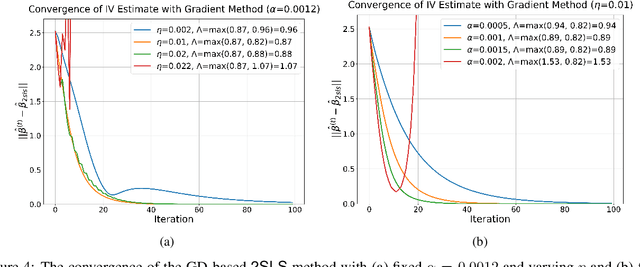
We explore the capability of transformers to address endogeneity in in-context linear regression. Our main finding is that transformers inherently possess a mechanism to handle endogeneity effectively using instrumental variables (IV). First, we demonstrate that the transformer architecture can emulate a gradient-based bi-level optimization procedure that converges to the widely used two-stage least squares $(\textsf{2SLS})$ solution at an exponential rate. Next, we propose an in-context pretraining scheme and provide theoretical guarantees showing that the global minimizer of the pre-training loss achieves a small excess loss. Our extensive experiments validate these theoretical findings, showing that the trained transformer provides more robust and reliable in-context predictions and coefficient estimates than the $\textsf{2SLS}$ method, in the presence of endogeneity.