ASGO: Adaptive Structured Gradient Optimization

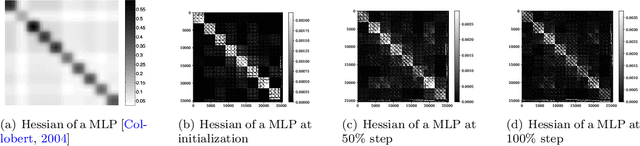
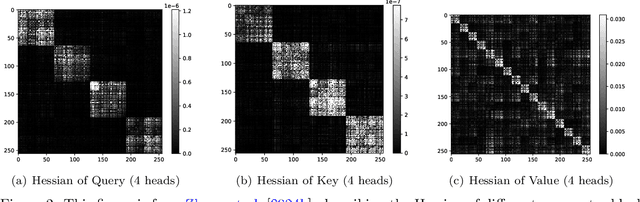
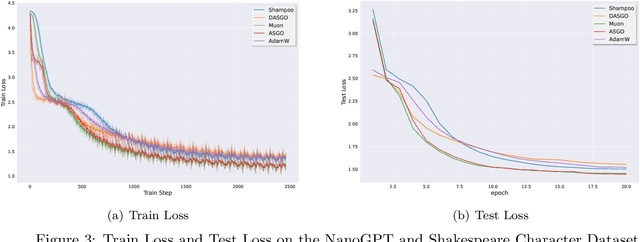
Training deep neural networks (DNNs) is a structured optimization problem, because the parameters are naturally represented by matrices and tensors rather than simple vectors. Under this structural representation, it has been widely observed that gradients are low-rank and Hessians are approximately block-wise diagonal. These structured properties are crucial for designing efficient optimization algorithms but may not be utilized by current popular optimizers like Adam. In this paper, we present a novel optimization algorithm ASGO that capitalizes on these properties by employing a preconditioner that is adaptively updated using structured gradients. By fine-grained theoretical analysis, ASGO is proven to achieve superior convergence rates compared to existing structured gradient methods. Based on the convergence theory, we further demonstrate that ASGO can benefit from the low-rank and block-wise diagonal properties. We also discuss practical modifications of ASGO and empirically verify the effectiveness of the algorithm on language model tasks.

Riemannian Proximal Sampler for High-accuracy Sampling on Manifolds

We introduce the Riemannian Proximal Sampler, a method for sampling from densities defined on Riemannian manifolds. The performance of this sampler critically depends on two key oracles: the Manifold Brownian Increments (MBI) oracle and the Riemannian Heat-kernel (RHK) oracle. We establish high-accuracy sampling guarantees for the Riemannian Proximal Sampler, showing that generating samples with $\varepsilon$-accuracy requires $O(\log(1/\varepsilon))$ iterations in Kullback-Leibler divergence assuming access to exact oracles and $O(\log^2(1/\varepsilon))$ iterations in the total variation metric assuming access to sufficiently accurate inexact oracles. Furthermore, we present practical implementations of these oracles by leveraging heat-kernel truncation and Varadhan's asymptotics. In the latter case, we interpret the Riemannian Proximal Sampler as a discretization of the entropy-regularized Riemannian Proximal Point Method on the associated Wasserstein space. We provide preliminary numerical results that illustrate the effectiveness of the proposed methodology.

Fully First-Order Methods for Decentralized Bilevel Optimization

This paper focuses on decentralized stochastic bilevel optimization (DSBO) where agents only communicate with their neighbors. We propose Decentralized Stochastic Gradient Descent and Ascent with Gradient Tracking (DSGDA-GT), a novel algorithm that only requires first-order oracles that are much cheaper than second-order oracles widely adopted in existing works. We further provide a finite-time convergence analysis showing that for $n$ agents collaboratively solving the DSBO problem, the sample complexity of finding an $\epsilon$-stationary point in our algorithm is $\mathcal{O}(n^{-1}\epsilon^{-7})$, which matches the currently best-known results of the single-agent counterpart with linear speedup. The numerical experiments demonstrate both the communication and training efficiency of our algorithm.

Single-Timescale Multi-Sequence Stochastic Approximation Without Fixed Point Smoothness: Theories and Applications

Stochastic approximation (SA) that involves multiple coupled sequences, known as multiple-sequence SA (MSSA), finds diverse applications in the fields of signal processing and machine learning. However, existing theoretical understandings {of} MSSA are limited: the multi-timescale analysis implies a slow convergence rate, whereas the single-timescale analysis relies on a stringent fixed point smoothness assumption. This paper establishes tighter single-timescale analysis for MSSA, without assuming smoothness of the fixed points. Our theoretical findings reveal that, when all involved operators are strongly monotone, MSSA converges at a rate of $\tilde{\mathcal{O}}(K^{-1})$, where $K$ denotes the total number of iterations. In addition, when all involved operators are strongly monotone except for the main one, MSSA converges at a rate of $\mathcal{O}(K^{-\frac{1}{2}})$. These theoretical findings align with those established for single-sequence SA. Applying these theoretical findings to bilevel optimization and communication-efficient distributed learning offers relaxed assumptions and/or simpler algorithms with performance guarantees, as validated by numerical experiments.

Tuning-Free Bilevel Optimization: New Algorithms and Convergence Analysis

Bilevel optimization has recently attracted considerable attention due to its abundant applications in machine learning problems. However, existing methods rely on prior knowledge of problem parameters to determine stepsizes, resulting in significant effort in tuning stepsizes when these parameters are unknown. In this paper, we propose two novel tuning-free algorithms, D-TFBO and S-TFBO. D-TFBO employs a double-loop structure with stepsizes adaptively adjusted by the "inverse of cumulative gradient norms" strategy. S-TFBO features a simpler fully single-loop structure that updates three variables simultaneously with a theory-motivated joint design of adaptive stepsizes for all variables. We provide a comprehensive convergence analysis for both algorithms and show that D-TFBO and S-TFBO respectively require $O(\frac{1}{\epsilon})$ and $O(\frac{1}{\epsilon}\log^4(\frac{1}{\epsilon}))$ iterations to find an $\epsilon$-accurate stationary point, (nearly) matching their well-tuned counterparts using the information of problem parameters. Experiments on various problems show that our methods achieve performance comparable to existing well-tuned approaches, while being more robust to the selection of initial stepsizes. To the best of our knowledge, our methods are the first to completely eliminate the need for stepsize tuning, while achieving theoretical guarantees.

Decentralized and Equitable Optimal Transport

This paper considers the decentralized (discrete) optimal transport (D-OT) problem. In this setting, a network of agents seeks to design a transportation plan jointly, where the cost function is the sum of privately held costs for each agent. We reformulate the D-OT problem as a constraint-coupled optimization problem and propose a single-loop decentralized algorithm with an iteration complexity of O(1/{\epsilon}) that matches existing centralized first-order approaches. Moreover, we propose the decentralized equitable optimal transport (DE-OT) problem. In DE-OT, in addition to cooperatively designing a transportation plan that minimizes transportation costs, agents seek to ensure equity in their individual costs. The iteration complexity of the proposed method to solve DE-OT is also O(1/{\epsilon}). This rate improves existing centralized algorithms, where the best iteration complexity obtained is O(1/{\epsilon}^2).

A Single-Loop Algorithm for Decentralized Bilevel Optimization

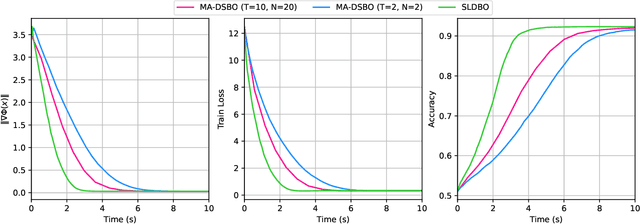
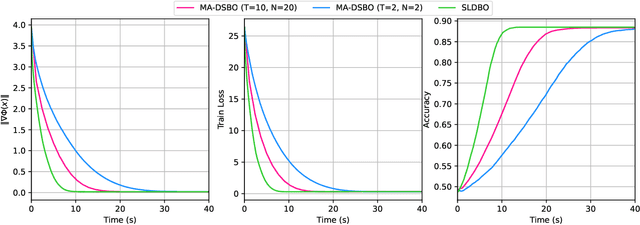
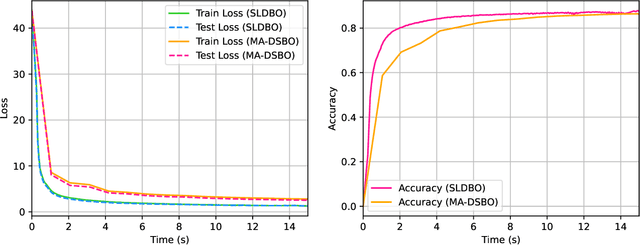
Bilevel optimization has received more and more attention recently due to its wide applications in machine learning. In this paper, we consider bilevel optimization in decentralized networks. In particular, we propose a novel single-loop algorithm for solving decentralized bilevel optimization with strongly convex lower level problem. Our algorithm is fully single-loop and does not require heavy matrix-vector multiplications when approximating the hypergradient. Moreover, unlike existing methods for decentralized bilevel optimization and federated bilevel optimization, our algorithm does not require any gradient heterogeneity assumption. Our analysis shows that the proposed algorithm achieves the best known convergence rate for bilevel optimization algorithms.

Zeroth-order Riemannian Averaging Stochastic Approximation Algorithms

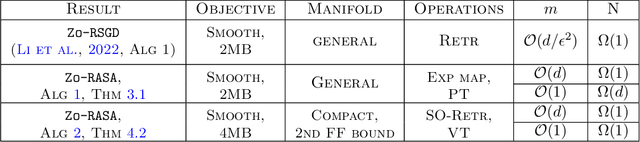
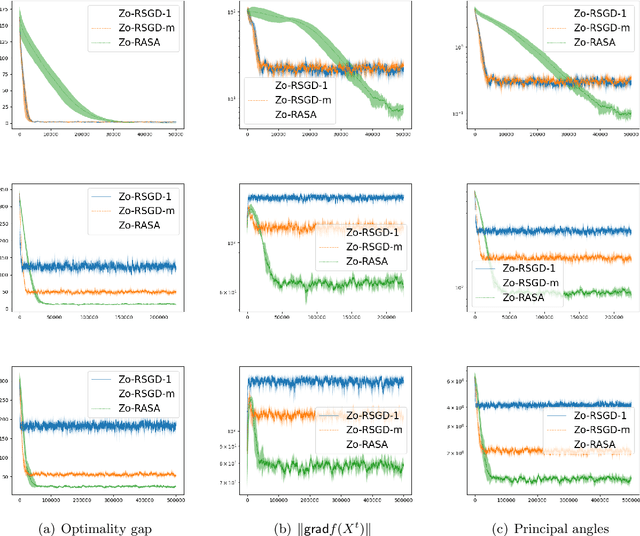
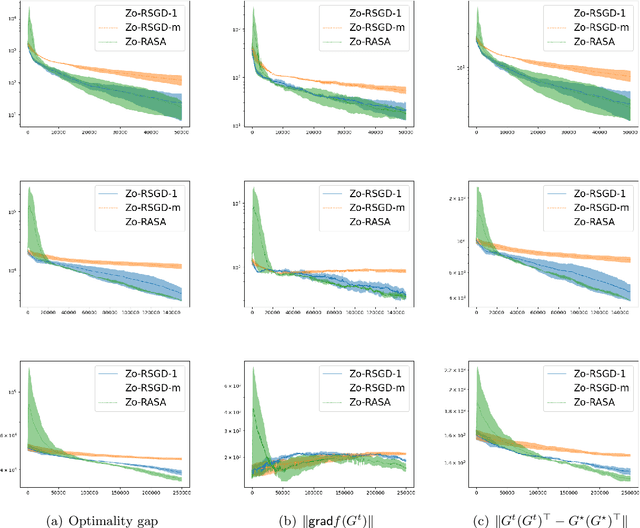
We present Zeroth-order Riemannian Averaging Stochastic Approximation (\texttt{Zo-RASA}) algorithms for stochastic optimization on Riemannian manifolds. We show that \texttt{Zo-RASA} achieves optimal sample complexities for generating $\epsilon$-approximation first-order stationary solutions using only one-sample or constant-order batches in each iteration. Our approach employs Riemannian moving-average stochastic gradient estimators, and a novel Riemannian-Lyapunov analysis technique for convergence analysis. We improve the algorithm's practicality by using retractions and vector transport, instead of exponential mappings and parallel transports, thereby reducing per-iteration complexity. Additionally, we introduce a novel geometric condition, satisfied by manifolds with bounded second fundamental form, which enables new error bounds for approximating parallel transport with vector transport.

A New Inexact Proximal Linear Algorithm with Adaptive Stopping Criteria for Robust Phase Retrieval

This paper considers the robust phase retrieval problem, which can be cast as a nonsmooth and nonconvex optimization problem. We propose a new inexact proximal linear algorithm with the subproblem being solved inexactly. Our contributions are two adaptive stopping criteria for the subproblem. The convergence behavior of the proposed methods is analyzed. Through experiments on both synthetic and real datasets, we demonstrate that our methods are much more efficient than existing methods, such as the original proximal linear algorithm and the subgradient method.

A Riemannian ADMM

We consider a class of Riemannian optimization problems where the objective is the sum of a smooth function and a nonsmooth function, considered in the ambient space. This class of problems finds important applications in machine learning and statistics such as the sparse principal component analysis, sparse spectral clustering, and orthogonal dictionary learning. We propose a Riemannian alternating direction method of multipliers (ADMM) to solve this class of problems. Our algorithm adopts easily computable steps in each iteration. The iteration complexity of the proposed algorithm for obtaining an $\epsilon$-stationary point is analyzed under mild assumptions. To the best of our knowledge, this is the first Riemannian ADMM with provable convergence guarantee for solving Riemannian optimization problem with nonsmooth objective. Numerical experiments are conducted to demonstrate the advantage of the proposed method.