Thinking on Maps: How Foundation Model Agents Explore, Remember, and Reason Map Environments

Map environments provide a fundamental medium for representing spatial structure. Understanding how foundation model (FM) agents understand and act in such environments is therefore critical for enabling reliable map-based reasoning and applications. However, most existing evaluations of spatial ability in FMs rely on static map inputs or text-based queries, overlooking the interactive and experience-driven nature of spatial understanding.In this paper, we propose an interactive evaluation framework to analyze how FM agents explore, remember, and reason in symbolic map environments. Agents incrementally explore partially observable grid-based maps consisting of roads, intersections, and points of interest (POIs), receiving only local observations at each step. Spatial understanding is then evaluated using six kinds of spatial tasks. By systematically varying exploration strategies, memory representations, and reasoning schemes across multiple foundation models, we reveal distinct functional roles of these components. Exploration primarily affects experience acquisition but has a limited impact on final reasoning accuracy. In contrast, memory representation plays a central role in consolidating spatial experience, with structured memories particularly sequential and graph-based representations, substantially improving performance on structure-intensive tasks such as path planning. Reasoning schemes further shape how stored spatial knowledge is used, with advanced prompts supporting more effective multi-step inference. We further observe that spatial reasoning performance saturates across model versions and scales beyond a certain capability threshold, indicating that improvements in map-based spatial understanding require mechanisms tailored to spatial representation and reasoning rather than scaling alone.

Theoretical Analysis on how Learning Rate Warmup Accelerates Convergence

Learning rate warmup is a popular and practical technique in training large-scale deep neural networks. Despite the huge success in practice, the theoretical advantages of this strategy of gradually increasing the learning rate at the beginning of the training process have not been fully understood. To resolve this gap between theory and practice, we first propose a novel family of generalized smoothness assumptions, and validate its applicability both theoretically and empirically. Under the novel smoothness assumption, we study the convergence properties of gradient descent (GD) in both deterministic and stochastic settings. It is shown that learning rate warmup consistently accelerates GD, and GD with warmup can converge at most $\Theta(T)$ times faster than with a non-increasing learning rate schedule in some specific cases, providing insights into the benefits of this strategy from an optimization theory perspective.

OoDDINO:A Multi-level Framework for Anomaly Segmentation on Complex Road Scenes

Anomaly segmentation aims to identify Out-of-Distribution (OoD) anomalous objects within images. Existing pixel-wise methods typically assign anomaly scores individually and employ a global thresholding strategy to segment anomalies. Despite their effectiveness, these approaches encounter significant challenges in real-world applications: (1) neglecting spatial correlations among pixels within the same object, resulting in fragmented segmentation; (2) variabil ity in anomaly score distributions across image regions, causing global thresholds to either generate false positives in background areas or miss segments of anomalous objects. In this work, we introduce OoDDINO, a novel multi-level anomaly segmentation framework designed to address these limitations through a coarse-to-fine anomaly detection strategy. OoDDINO combines an uncertainty-guided anomaly detection model with a pixel-level segmentation model within a two-stage cascade architecture. Initially, we propose an Orthogonal Uncertainty-Aware Fusion Strategy (OUAFS) that sequentially integrates multiple uncertainty metrics with visual representations, employing orthogonal constraints to strengthen the detection model's capacity for localizing anomalous regions accurately. Subsequently, we develop an Adaptive Dual-Threshold Network (ADT-Net), which dynamically generates region-specific thresholds based on object-level detection outputs and pixel-wise anomaly scores. This approach allows for distinct thresholding strategies within foreground and background areas, achieving fine-grained anomaly segmentation. The proposed framework is compatible with other pixel-wise anomaly detection models, which acts as a plug-in to boost the performance. Extensive experiments on two benchmark datasets validate our framework's superiority and compatibility over state-of-the-art methods.

ASGO: Adaptive Structured Gradient Optimization

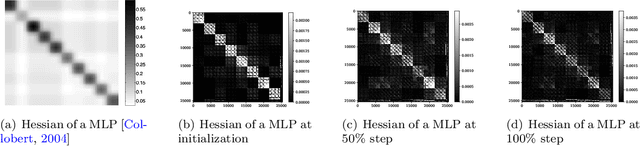
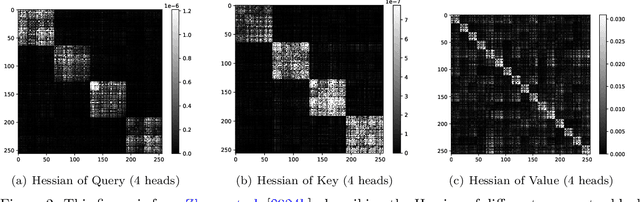
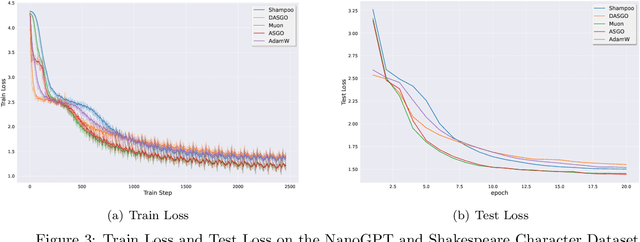
Training deep neural networks (DNNs) is a structured optimization problem, because the parameters are naturally represented by matrices and tensors rather than simple vectors. Under this structural representation, it has been widely observed that gradients are low-rank and Hessians are approximately block-wise diagonal. These structured properties are crucial for designing efficient optimization algorithms but may not be utilized by current popular optimizers like Adam. In this paper, we present a novel optimization algorithm ASGO that capitalizes on these properties by employing a preconditioner that is adaptively updated using structured gradients. By fine-grained theoretical analysis, ASGO is proven to achieve superior convergence rates compared to existing structured gradient methods. Based on the convergence theory, we further demonstrate that ASGO can benefit from the low-rank and block-wise diagonal properties. We also discuss practical modifications of ASGO and empirically verify the effectiveness of the algorithm on language model tasks.

Large Batch Analysis for Adagrad Under Anisotropic Smoothness

Adaptive gradient algorithms have been widely adopted in training large-scale deep neural networks, especially large foundation models. Despite their huge success in practice, their theoretical advantages over stochastic gradient descent (SGD) have not been fully understood, especially in the large batch-size setting commonly used in practice. This is because the only theoretical result that can demonstrate the benefit of Adagrad over SGD was obtained in the original paper of Adagrad for nonsmooth objective functions. However, for nonsmooth objective functions, there can be a linear slowdown of convergence when batch size increases, and thus a convergence analysis based on nonsmooth assumption cannot be used for large batch algorithms. In this work, we resolve this gap between theory and practice by providing a new analysis of Adagrad on both convex and nonconvex smooth objectives suitable for the large batch setting. It is shown that under the anisotropic smoothness and noise conditions, increased batch size does not slow down convergence for Adagrad, and thus it can still achieve a faster convergence guarantee over SGD even in the large batch setting. We present detailed comparisons between SGD and Adagrad to provide a better understanding of the benefits of adaptive gradient methods. Experiments in logistic regression and instruction following fine-tuning tasks provide strong evidence to support our theoretical analysis.

On the Complexity of Finite-Sum Smooth Optimization under the Polyak-Łojasiewicz Condition

This paper considers the optimization problem of the form $\min_{{\bf x}\in{\mathbb R}^d} f({\bf x})\triangleq \frac{1}{n}\sum_{i=1}^n f_i({\bf x})$, where $f(\cdot)$ satisfies the Polyak--{\L}ojasiewicz (PL) condition with parameter $\mu$ and $\{f_i(\cdot)\}_{i=1}^n$ is $L$-mean-squared smooth. We show that any gradient method requires at least $\Omega(n+\kappa\sqrt{n}\log(1/\epsilon))$ incremental first-order oracle (IFO) calls to find an $\epsilon$-suboptimal solution, where $\kappa\triangleq L/\mu$ is the condition number of the problem. This result nearly matches upper bounds of IFO complexity for best-known first-order methods. We also study the problem of minimizing the PL function in the distributed setting such that the individuals $f_1(\cdot),\dots,f_n(\cdot)$ are located on a connected network of $n$ agents. We provide lower bounds of $\Omega(\kappa/\sqrt{\gamma}\,\log(1/\epsilon))$, $\Omega((\kappa+\tau\kappa/\sqrt{\gamma}\,)\log(1/\epsilon))$ and $\Omega\big(n+\kappa\sqrt{n}\log(1/\epsilon)\big)$ for communication rounds, time cost and local first-order oracle calls respectively, where $\gamma\in(0,1]$ is the spectral gap of the mixing matrix associated with the network and~$\tau>0$ is the time cost of per communication round. Furthermore, we propose a decentralized first-order method that nearly matches above lower bounds in expectation.

Accelerated Convergence of Stochastic Heavy Ball Method under Anisotropic Gradient Noise

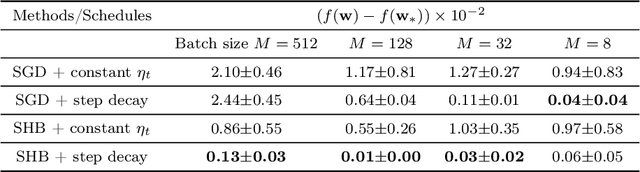
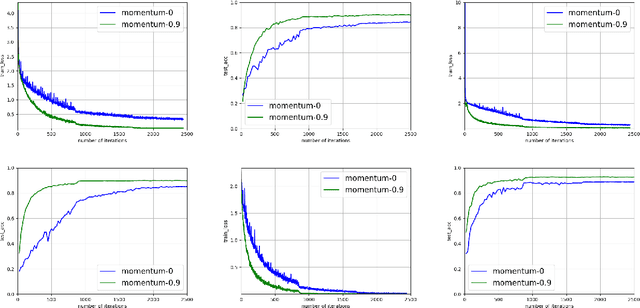
Heavy-ball momentum with decaying learning rates is widely used with SGD for optimizing deep learning models. In contrast to its empirical popularity, the understanding of its theoretical property is still quite limited, especially under the standard anisotropic gradient noise condition for quadratic regression problems. Although it is widely conjectured that heavy-ball momentum method can provide accelerated convergence and should work well in large batch settings, there is no rigorous theoretical analysis. In this paper, we fill this theoretical gap by establishing a non-asymptotic convergence bound for stochastic heavy-ball methods with step decay scheduler on quadratic objectives, under the anisotropic gradient noise condition. As a direct implication, we show that heavy-ball momentum can provide $\tilde{\mathcal{O}}(\sqrt{\kappa})$ accelerated convergence of the bias term of SGD while still achieving near-optimal convergence rate with respect to the stochastic variance term. The combined effect implies an overall convergence rate within log factors from the statistical minimax rate. This means SGD with heavy-ball momentum is useful in the large-batch settings such as distributed machine learning or federated learning, where a smaller number of iterations can significantly reduce the number of communication rounds, leading to acceleration in practice.