Decentralized Non-convex Stochastic Optimization with Heterogeneous Variance

Decentralized optimization is critical for solving large-scale machine learning problems over distributed networks, where multiple nodes collaborate through local communication. In practice, the variances of stochastic gradient estimators often differ across nodes, yet their impact on algorithm design and complexity remains unclear. To address this issue, we propose D-NSS, a decentralized algorithm with node-specific sampling, and establish its sample complexity depending on the arithmetic mean of local standard deviations, achieving tighter bounds than existing methods that rely on the worst-case or quadratic mean. We further derive a matching sample complexity lower bound under heterogeneous variance, thereby proving the optimality of this dependence. Moreover, we extend the framework with a variance reduction technique and develop D-NSS-VR, which under the mean-squared smoothness assumption attains an improved sample complexity bound while preserving the arithmetic-mean dependence. Finally, numerical experiments validate the theoretical results and demonstrate the effectiveness of the proposed algorithms.

Sign-Based Optimizers Are Effective Under Heavy-Tailed Noise

While adaptive gradient methods are the workhorse of modern machine learning, sign-based optimization algorithms such as Lion and Muon have recently demonstrated superior empirical performance over AdamW in training large language models (LLM). However, a theoretical understanding of why sign-based updates outperform variance-adapted methods remains elusive. In this paper, we aim to bridge the gap between theory and practice through the lens of heavy-tailed gradient noise, a phenomenon frequently observed in language modeling tasks. Theoretically, we introduce a novel generalized heavy-tailed noise condition that captures the behavior of LLMs more accurately than standard finite variance assumptions. Under this noise model, we establish sharp convergence rates of SignSGD and Lion for generalized smooth function classes, matching or surpassing previous best-known bounds. Furthermore, we extend our analysis to Muon and Muonlight, providing what is, to our knowledge, the first rigorous analysis of matrix optimization under heavy-tailed stochasticity. These results offer a strong theoretical justification for the empirical superiority of sign-based optimizers, showcasing that they are naturally suited to handle the noisy gradients associated with heavy tails. Empirically, LLM pretraining experiments validate our theoretical insights and confirm that our proposed noise models are well-aligned with practice.

Optimal Asynchronous Stochastic Nonconvex Optimization under Heavy-Tailed Noise

This paper considers the problem of asynchronous stochastic nonconvex optimization with heavy-tailed gradient noise and arbitrarily heterogeneous computation times across workers. We propose an asynchronous normalized stochastic gradient descent algorithm with momentum. The analysis show that our method achieves the optimal time complexity under the assumption of bounded $p$th-order central moment with $p\in(1,2]$. We also provide numerical experiments to show the effectiveness of proposed method.

Stability and Generalization of Nonconvex Optimization with Heavy-Tailed Noise

The empirical evidence indicates that stochastic optimization with heavy-tailed gradient noise is more appropriate to characterize the training of machine learning models than that with standard bounded gradient variance noise. Most existing works on this phenomenon focus on the convergence of optimization errors, while the analysis for generalization bounds under the heavy-tailed gradient noise remains limited. In this paper, we develop a general framework for establishing generalization bounds under heavy-tailed noise. Specifically, we introduce a truncation argument to achieve the generalization error bound based on the algorithmic stability under the assumption of bounded $p$th centered moment with $p\in(1,2]$. Building on this framework, we further provide the stability and generalization analysis for several popular stochastic algorithms under heavy-tailed noise, including clipped and normalized stochastic gradient descent, as well as their mini-batch and momentum variants.

Near-Optimal Decentralized Stochastic Nonconvex Optimization with Heavy-Tailed Noise

This paper studies decentralized stochastic nonconvex optimization problem over row-stochastic networks. We consider the heavy-tailed gradient noise which is empirically observed in many popular real-world applications. Specifically, we propose a decentralized normalized stochastic gradient descent with Pull-Diag gradient tracking, which achieves approximate stationary points with the optimal sample complexity and the near-optimal communication complexity. We further follow our framework to study the setting of undirected networks, also achieving the nearly tight upper complexity bounds. Moreover, we conduct empirical studies to show the practical superiority of the proposed methods.

Accelerated Evolving Set Processes for Local PageRank Computation

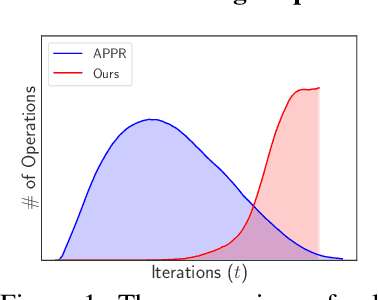
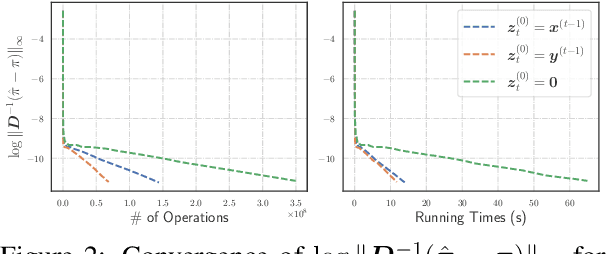
This work proposes a novel framework based on nested evolving set processes to accelerate Personalized PageRank (PPR) computation. At each stage of the process, we employ a localized inexact proximal point iteration to solve a simplified linear system. We show that the time complexity of such localized methods is upper bounded by $\min\{\tilde{\mathcal{O}}(R^2/\epsilon^2), \tilde{\mathcal{O}}(m)\}$ to obtain an $\epsilon$-approximation of the PPR vector, where $m$ denotes the number of edges in the graph and $R$ is a constant defined via nested evolving set processes. Furthermore, the algorithms induced by our framework require solving only $\tilde{\mathcal{O}}(1/\sqrt{\alpha})$ such linear systems, where $\alpha$ is the damping factor. When $1/\epsilon^2\ll m$, this implies the existence of an algorithm that computes an $\ epsilon $-approximation of the PPR vector with an overall time complexity of $\tilde{\mathcal{O}}\left(R^2 / (\sqrt{\alpha}\epsilon^2)\right)$, independent of the underlying graph size. Our result resolves an open conjecture from existing literature. Experimental results on real-world graphs validate the efficiency of our methods, demonstrating significant convergence in the early stages.

Stochastic Bilevel Optimization with Heavy-Tailed Noise

This paper considers the smooth bilevel optimization in which the lower-level problem is strongly convex and the upper-level problem is possibly nonconvex. We focus on the stochastic setting that the algorithm can access the unbiased stochastic gradient evaluation with heavy-tailed noise, which is prevalent in many machine learning applications such as training large language models and reinforcement learning. We propose a nested-loop normalized stochastic bilevel approximation (N$^2$SBA) for finding an $\epsilon$-stationary point with the stochastic first-order oracle (SFO) complexity of $\tilde{\mathcal{O}}\big(\kappa^{\frac{7p-3}{p-1}} \sigma^{\frac{p}{p-1}} \epsilon^{-\frac{4 p - 2}{p-1}}\big)$, where $\kappa$ is the condition number, $p\in(1,2]$ is the order of central moment for the noise, and $\sigma$ is the noise level. Furthermore, we specialize our idea to solve the nonconvex-strongly-concave minimax optimization problem, achieving an $\epsilon$-stationary point with the SFO complexity of $\tilde{\mathcal O}\big(\kappa^{\frac{2p-1}{p-1}} \sigma^{\frac{p}{p-1}} \epsilon^{-\frac{3p-2}{p-1}}\big)$. All above upper bounds match the best-known results under the special case of the bounded variance setting, i.e., $p=2$.

Decentralized Stochastic Nonconvex Optimization under the Relaxed Smoothness

This paper studies decentralized optimization problem $f(\mathbf{x})=\frac{1}{m}\sum_{i=1}^m f_i(\mathbf{x})$, where each local function has the form of $f_i(\mathbf{x}) = {\mathbb E}\left[F(\mathbf{x};{\xi}_i)\right]$ which is $(L_0,L_1)$-smooth but possibly nonconvex and the random variable ${\xi}_i$ follows distribution ${\mathcal D}_i$. We propose a novel algorithm called decentralized normalized stochastic gradient descent (DNSGD), which can achieve the $\epsilon$-stationary point on each local agent. We present a new framework for analyzing decentralized first-order methods in the relaxed smooth setting, based on the Lyapunov function related to the product of the gradient norm and the consensus error. The analysis shows upper bounds on sample complexity of ${\mathcal O}(m^{-1}(L_f\sigma^2\Delta_f\epsilon^{-4} + \sigma^2\epsilon^{-2} + L_f^{-2}L_1^3\sigma^2\Delta_f\epsilon^{-1} + L_f^{-2}L_1^2\sigma^2))$ per agent and communication complexity of $\tilde{\mathcal O}((L_f\epsilon^{-2} + L_1\epsilon^{-1})\gamma^{-1/2}\Delta_f)$, where $L_f=L_0 +L_1\zeta$, $\sigma^2$ is the variance of the stochastic gradient, $\Delta_f$ is the initial optimal function value gap, $\gamma$ is the spectral gap of the network, and $\zeta$ is the degree of the gradient dissimilarity. In the special case of $L_1=0$, the above results (nearly) match the lower bounds on decentralized nonconvex optimization in the standard smooth setting. We also conduct numerical experiments to show the empirical superiority of our method.

Solving Convex-Concave Problems with $\tilde{\mathcal{O}}(ε^{-4/7})$ Second-Order Oracle Complexity

Previous algorithms can solve convex-concave minimax problems $\min_{x \in \mathcal{X}} \max_{y \in \mathcal{Y}} f(x,y)$ with $\mathcal{O}(\epsilon^{-2/3})$ second-order oracle calls using Newton-type methods. This result has been speculated to be optimal because the upper bound is achieved by a natural generalization of the optimal first-order method. In this work, we show an improved upper bound of $\tilde{\mathcal{O}}(\epsilon^{-4/7})$ by generalizing the optimal second-order method for convex optimization to solve the convex-concave minimax problem. We further apply a similar technique to lazy Hessian algorithms and show that our proposed algorithm can also be seen as a second-order ``Catalyst'' framework (Lin et al., JMLR 2018) that could accelerate any globally convergent algorithms for solving minimax problems.

Incremental Gauss--Newton Methods with Superlinear Convergence Rates

This paper addresses the challenge of solving large-scale nonlinear equations with H\"older continuous Jacobians. We introduce a novel Incremental Gauss--Newton (IGN) method within explicit superlinear convergence rate, which outperforms existing methods that only achieve linear convergence rate. In particular, we formulate our problem by the nonlinear least squares with finite-sum structure, and our method incrementally iterates with the information of one component in each round. We also provide a mini-batch extension to our IGN method that obtains an even faster superlinear convergence rate. Furthermore, we conduct numerical experiments to show the advantages of the proposed methods.