Baojian Zhou
Logics-STEM: Empowering LLM Reasoning via Failure-Driven Post-Training and Document Knowledge Enhancement
Jan 08, 2026Abstract:We present Logics-STEM, a state-of-the-art reasoning model fine-tuned on Logics-STEM-SFT-Dataset, a high-quality and diverse dataset at 10M scale that represents one of the largest-scale open-source long chain-of-thought corpora. Logics-STEM targets reasoning tasks in the domains of Science, Technology, Engineering, and Mathematics (STEM), and exhibits exceptional performance on STEM-related benchmarks with an average improvement of 4.68% over the next-best model at 8B scale. We attribute the gains to our data-algorithm co-design engine, where they are jointly optimized to fit a gold-standard distribution behind reasoning. Data-wise, the Logics-STEM-SFT-Dataset is constructed from a meticulously designed data curation engine with 5 stages to ensure the quality, diversity, and scalability, including annotation, deduplication, decontamination, distillation, and stratified sampling. Algorithm-wise, our failure-driven post-training framework leverages targeted knowledge retrieval and data synthesis around model failure regions in the Supervised Fine-tuning (SFT) stage to effectively guide the second-stage SFT or the reinforcement learning (RL) for better fitting the target distribution. The superior empirical performance of Logics-STEM reveals the vast potential of combining large-scale open-source data with carefully designed synthetic data, underscoring the critical role of data-algorithm co-design in enhancing reasoning capabilities through post-training. We make both the Logics-STEM models (8B and 32B) and the Logics-STEM-SFT-Dataset (10M and downsampled 2.2M versions) publicly available to support future research in the open-source community.
Accelerated Evolving Set Processes for Local PageRank Computation
Oct 09, 2025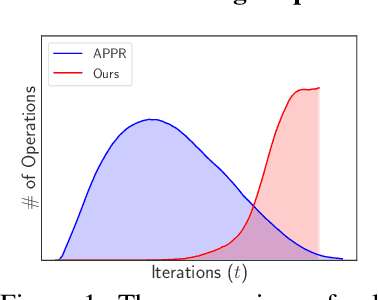

Abstract:This work proposes a novel framework based on nested evolving set processes to accelerate Personalized PageRank (PPR) computation. At each stage of the process, we employ a localized inexact proximal point iteration to solve a simplified linear system. We show that the time complexity of such localized methods is upper bounded by $\min\{\tilde{\mathcal{O}}(R^2/\epsilon^2), \tilde{\mathcal{O}}(m)\}$ to obtain an $\epsilon$-approximation of the PPR vector, where $m$ denotes the number of edges in the graph and $R$ is a constant defined via nested evolving set processes. Furthermore, the algorithms induced by our framework require solving only $\tilde{\mathcal{O}}(1/\sqrt{\alpha})$ such linear systems, where $\alpha$ is the damping factor. When $1/\epsilon^2\ll m$, this implies the existence of an algorithm that computes an $\ epsilon $-approximation of the PPR vector with an overall time complexity of $\tilde{\mathcal{O}}\left(R^2 / (\sqrt{\alpha}\epsilon^2)\right)$, independent of the underlying graph size. Our result resolves an open conjecture from existing literature. Experimental results on real-world graphs validate the efficiency of our methods, demonstrating significant convergence in the early stages.
Fast and Robust Contextual Node Representation Learning over Dynamic Graphs
Nov 11, 2024



Abstract:Real-world graphs grow rapidly with edge and vertex insertions over time, motivating the problem of efficiently maintaining robust node representation over evolving graphs. Recent efficient GNNs are designed to decouple recursive message passing from the learning process, and favor Personalized PageRank (PPR) as the underlying feature propagation mechanism. However, most PPR-based GNNs are designed for static graphs, and efficient PPR maintenance remains as an open problem. Further, there is surprisingly little theoretical justification for the choice of PPR, despite its impressive empirical performance. In this paper, we are inspired by the recent PPR formulation as an explicit $\ell_1$-regularized optimization problem and propose a unified dynamic graph learning framework based on sparse node-wise attention. We also present a set of desired properties to justify the choice of PPR in STOA GNNs, and serves as the guideline for future node attention designs. Meanwhile, we take advantage of the PPR-equivalent optimization formulation and employ the proximal gradient method (ISTA) to improve the efficiency of PPR-based GNNs upto 6 times. Finally, we instantiate a simple-yet-effective model (\textsc{GoPPE}) with robust positional encodings by maximizing PPR previously used as attention. The model performs comparably to or better than the STOA baselines and greatly outperforms when the initial node attributes are noisy during graph evolution, demonstrating the effectiveness and robustness of \textsc{GoPPE}.
Faster Local Solvers for Graph Diffusion Equations
Oct 29, 2024



Abstract:Efficient computation of graph diffusion equations (GDEs), such as Personalized PageRank, Katz centrality, and the Heat kernel, is crucial for clustering, training neural networks, and many other graph-related problems. Standard iterative methods require accessing the whole graph per iteration, making them time-consuming for large-scale graphs. While existing local solvers approximate diffusion vectors through heuristic local updates, they often operate sequentially and are typically designed for specific diffusion types, limiting their applicability. Given that diffusion vectors are highly localizable, as measured by the participation ratio, this paper introduces a novel framework for approximately solving GDEs using a local diffusion process. This framework reveals the suboptimality of existing local solvers. Furthermore, our approach effectively localizes standard iterative solvers by designing simple and provably sublinear time algorithms. These new local solvers are highly parallelizable, making them well-suited for implementation on GPUs. We demonstrate the effectiveness of our framework in quickly obtaining approximate diffusion vectors, achieving up to a hundred-fold speed improvement, and its applicability to large-scale dynamic graphs. Our framework could also facilitate more efficient local message-passing mechanisms for GNNs.
Iterative Methods via Locally Evolving Set Process
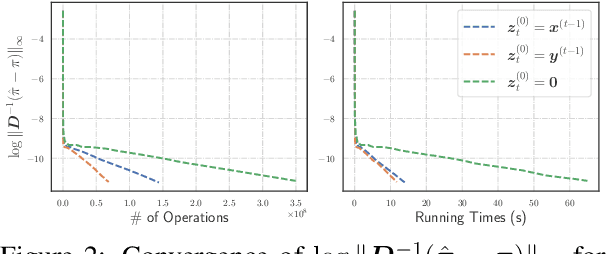
Oct 19, 2024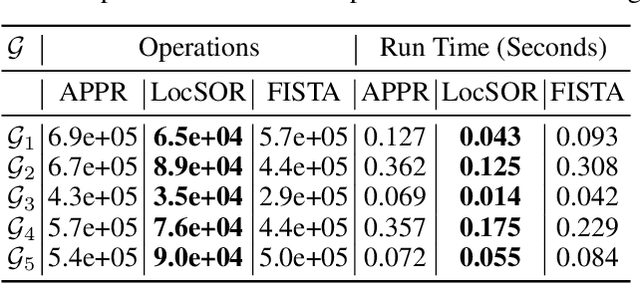
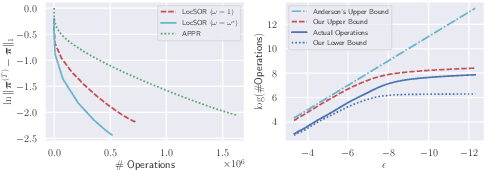


Abstract:Given the damping factor $\alpha$ and precision tolerance $\epsilon$, \citet{andersen2006local} introduced Approximate Personalized PageRank (APPR), the \textit{de facto local method} for approximating the PPR vector, with runtime bounded by $\Theta(1/(\alpha\epsilon))$ independent of the graph size. Recently, \citet{fountoulakis2022open} asked whether faster local algorithms could be developed using $\tilde{O}(1/(\sqrt{\alpha}\epsilon))$ operations. By noticing that APPR is a local variant of Gauss-Seidel, this paper explores the question of \textit{whether standard iterative solvers can be effectively localized}. We propose to use the \textit{locally evolving set process}, a novel framework to characterize the algorithm locality, and demonstrate that many standard solvers can be effectively localized. Let $\overline{\operatorname{vol}}{ (S_t)}$ and $\overline{\gamma}_{t}$ be the running average of volume and the residual ratio of active nodes $\textstyle S_{t}$ during the process. We show $\overline{\operatorname{vol}}{ (S_t)}/\overline{\gamma}_{t} \leq 1/\epsilon$ and prove APPR admits a new runtime bound $\tilde{O}(\overline{\operatorname{vol}}(S_t)/(\alpha\overline{\gamma}_{t}))$ mirroring the actual performance. Furthermore, when the geometric mean of residual reduction is $\Theta(\sqrt{\alpha})$, then there exists $c \in (0,2)$ such that the local Chebyshev method has runtime $\tilde{O}(\overline{\operatorname{vol}}(S_{t})/(\sqrt{\alpha}(2-c)))$ without the monotonicity assumption. Numerical results confirm the efficiency of this novel framework and show up to a hundredfold speedup over corresponding standard solvers on real-world graphs.
Sensiverse: A dataset for ISAC study
Aug 26, 2023



Abstract:In order to address the lack of applicable channel models for ISAC research and evaluation, we release Sensiverse, a dataset that can be used for ISAC research. In this paper, we present the method of generating Sensiverse, including the acquisition and formatting of the 3D scene models, the generation of the channel data and associations with Tx/Rx deployment. The file structure and usage of the dataset are also described, and finally the use of the dataset is illustrated with examples through the evaluation of use cases such as 3D environment reconstruction and moving targets.
Does it pay to optimize AUC?
Jun 02, 2023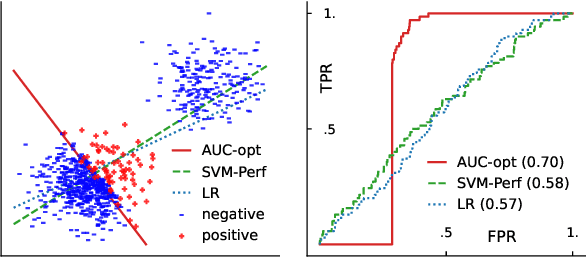
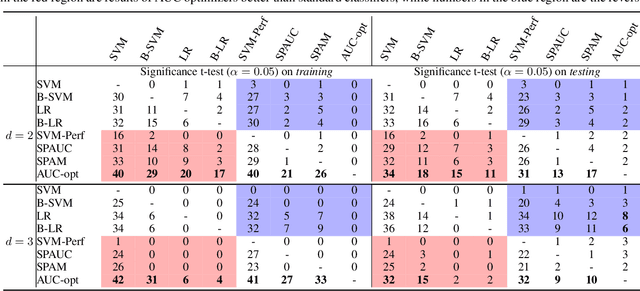
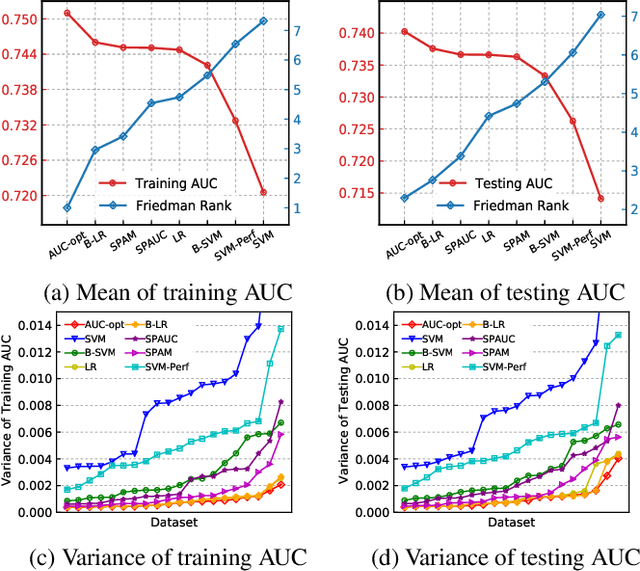
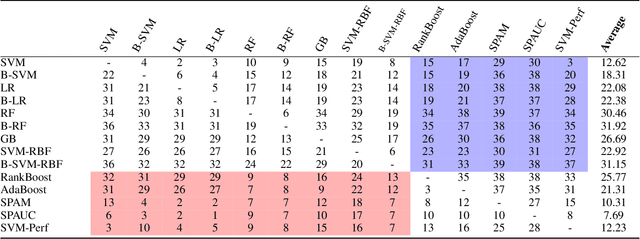
Abstract:The Area Under the ROC Curve (AUC) is an important model metric for evaluating binary classifiers, and many algorithms have been proposed to optimize AUC approximately. It raises the question of whether the generally insignificant gains observed by previous studies are due to inherent limitations of the metric or the inadequate quality of optimization. To better understand the value of optimizing for AUC, we present an efficient algorithm, namely AUC-opt, to find the provably optimal AUC linear classifier in $\mathbb{R}^2$, which runs in $\mathcal{O}(n_+ n_- \log (n_+ n_-))$ where $n_+$ and $n_-$ are the number of positive and negative samples respectively. Furthermore, it can be naturally extended to $\mathbb{R}^d$ in $\mathcal{O}((n_+n_-)^{d-1}\log (n_+n_-))$ by calling AUC-opt in lower-dimensional spaces recursively. We prove the problem is NP-complete when $d$ is not fixed, reducing from the \textit{open hemisphere problem}. Experiments show that compared with other methods, AUC-opt achieves statistically significant improvements on between 17 to 40 in $\mathbb{R}^2$ and between 4 to 42 in $\mathbb{R}^3$ of 50 t-SNE training datasets. However, generally the gain proves insignificant on most testing datasets compared to the best standard classifiers. Similar observations are found for nonlinear AUC methods under real-world datasets.
Fast Online Node Labeling for Very Large Graphs
May 25, 2023



Abstract:This paper studies the online node classification problem under a transductive learning setting. Current methods either invert a graph kernel matrix with $\mathcal{O}(n^3)$ runtime and $\mathcal{O}(n^2)$ space complexity or sample a large volume of random spanning trees, thus are difficult to scale to large graphs. In this work, we propose an improvement based on the \textit{online relaxation} technique introduced by a series of works (Rakhlin et al.,2012; Rakhlin and Sridharan, 2015; 2017). We first prove an effective regret $\mathcal{O}(\sqrt{n^{1+\gamma}})$ when suitable parameterized graph kernels are chosen, then propose an approximate algorithm FastONL enjoying $\mathcal{O}(k\sqrt{n^{1+\gamma}})$ regret based on this relaxation. The key of FastONL is a \textit{generalized local push} method that effectively approximates inverse matrix columns and applies to a series of popular kernels. Furthermore, the per-prediction cost is $\mathcal{O}(\text{vol}({\mathcal{S}})\log 1/\epsilon)$ locally dependent on the graph with linear memory cost. Experiments show that our scalable method enjoys a better tradeoff between local and global consistency.
Approximate Frank-Wolfe Algorithms over Graph-structured Support Sets
Jun 29, 2021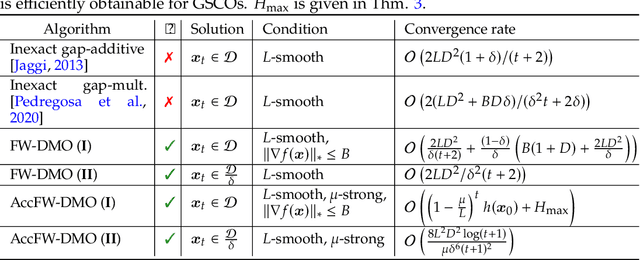
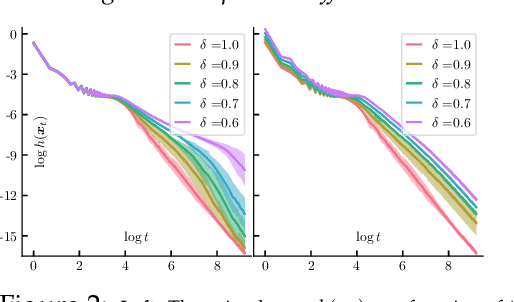
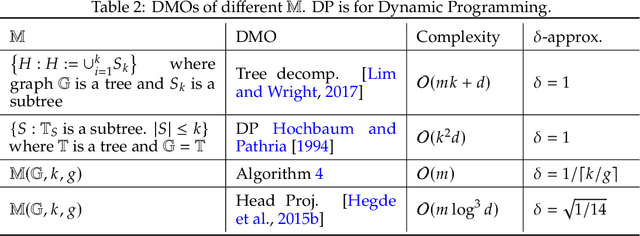
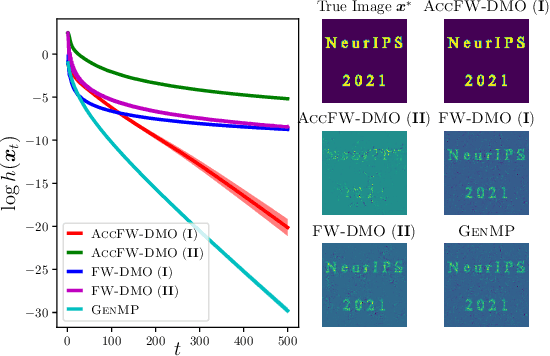
Abstract:In this paper, we propose approximate Frank-Wolfe (FW) algorithms to solve convex optimization problems over graph-structured support sets where the \textit{linear minimization oracle} (LMO) cannot be efficiently obtained in general. We first demonstrate that two popular approximation assumptions (\textit{additive} and \textit{multiplicative gap errors)}, are not valid for our problem, in that no cheap gap-approximate LMO oracle exists in general. Instead, a new \textit{approximate dual maximization oracle} (DMO) is proposed, which approximates the inner product rather than the gap. When the objective is $L$-smooth, we prove that the standard FW method using a $\delta$-approximate DMO converges as $\mathcal{O}(L / \delta t + (1-\delta)(\delta^{-1} + \delta^{-2}))$ in general, and as $\mathcal{O}(L/(\delta^2(t+2)))$ over a $\delta$-relaxation of the constraint set. Additionally, when the objective is $\mu$-strongly convex and the solution is unique, a variant of FW converges to $\mathcal{O}(L^2\log(t)/(\mu \delta^6 t^2))$ with the same per-iteration complexity. Our empirical results suggest that even these improved bounds are pessimistic, with significant improvement in recovering real-world images with graph-structured sparsity.
Stochastic Hard Thresholding Algorithms for AUC Maximization
Nov 04, 2020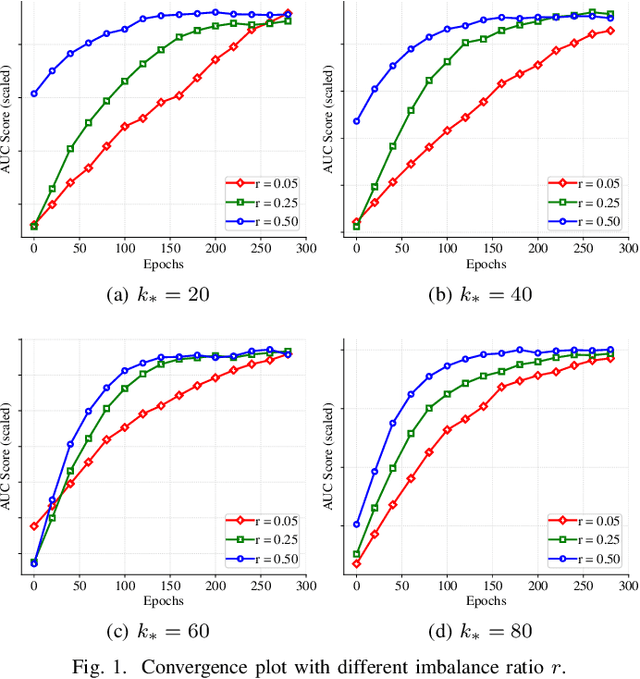
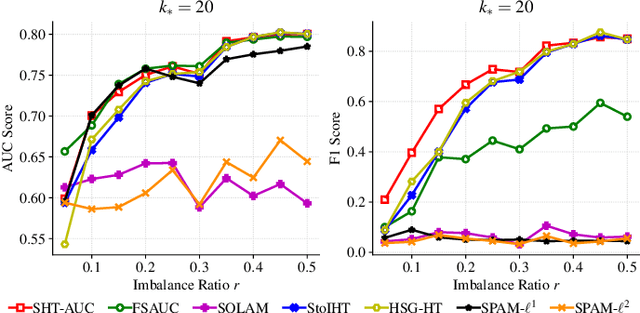
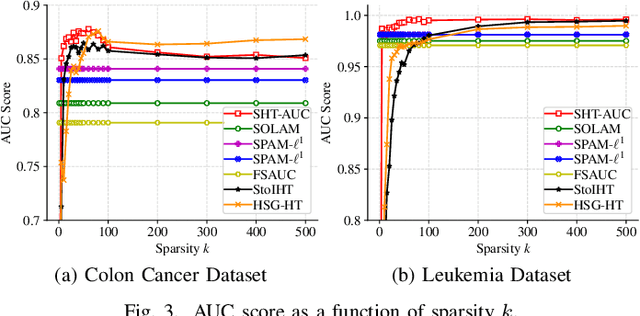
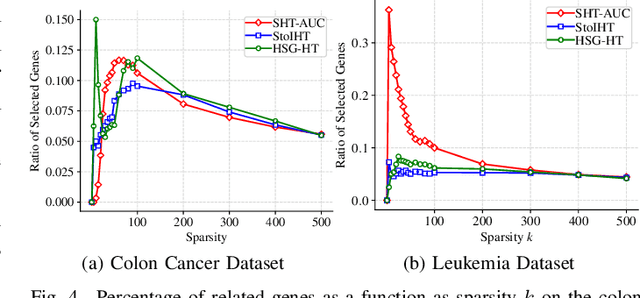
Abstract:In this paper, we aim to develop stochastic hard thresholding algorithms for the important problem of AUC maximization in imbalanced classification. The main challenge is the pairwise loss involved in AUC maximization. We overcome this obstacle by reformulating the U-statistics objective function as an empirical risk minimization (ERM), from which a stochastic hard thresholding algorithm (\texttt{SHT-AUC}) is developed. To our best knowledge, this is the first attempt to provide stochastic hard thresholding algorithms for AUC maximization with a per-iteration cost $\O(b d)$ where $d$ and $b$ are the dimension of the data and the minibatch size, respectively. We show that the proposed algorithm enjoys the linear convergence rate up to a tolerance error. In particular, we show, if the data is generated from the Gaussian distribution, then its convergence becomes slower as the data gets more imbalanced. We conduct extensive experiments to show the efficiency and effectiveness of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge