Robust COVID-19 Detection in CT Images with CLIP

In the realm of medical imaging, particularly for COVID-19 detection, deep learning models face substantial challenges such as the necessity for extensive computational resources, the paucity of well-annotated datasets, and a significant amount of unlabeled data. In this work, we introduce the first lightweight detector designed to overcome these obstacles, leveraging a frozen CLIP image encoder and a trainable multilayer perception (MLP). Enhanced with Conditional Value at Risk (CVaR) for robustness and a loss landscape flattening strategy for improved generalization, our model is tailored for high efficacy in COVID-19 detection. Furthermore, we integrate a teacher-student framework to capitalize on the vast amounts of unlabeled data, enabling our model to achieve superior performance despite the inherent data limitations. Experimental results on the COV19-CT-DB dataset demonstrate the effectiveness of our approach, surpassing baseline by up to 10.6% in `macro' F1 score in supervised learning. The code is available at https://github.com/Purdue-M2/COVID-19_Detection_M2_PURDUE.

Outlier Robust Adversarial Training

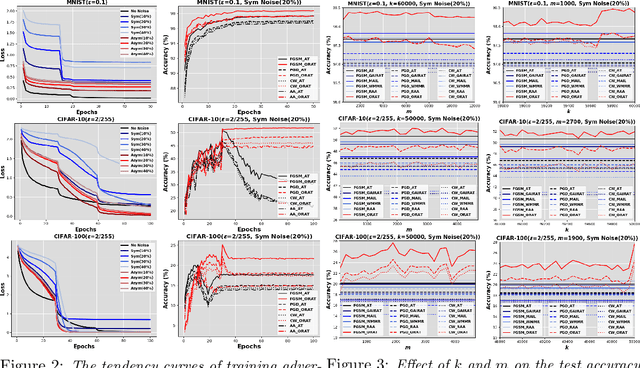
Supervised learning models are challenged by the intrinsic complexities of training data such as outliers and minority subpopulations and intentional attacks at inference time with adversarial samples. While traditional robust learning methods and the recent adversarial training approaches are designed to handle each of the two challenges, to date, no work has been done to develop models that are robust with regard to the low-quality training data and the potential adversarial attack at inference time simultaneously. It is for this reason that we introduce Outlier Robust Adversarial Training (ORAT) in this work. ORAT is based on a bi-level optimization formulation of adversarial training with a robust rank-based loss function. Theoretically, we show that the learning objective of ORAT satisfies the $\mathcal{H}$-consistency in binary classification, which establishes it as a proper surrogate to adversarial 0/1 loss. Furthermore, we analyze its generalization ability and provide uniform convergence rates in high probability. ORAT can be optimized with a simple algorithm. Experimental evaluations on three benchmark datasets demonstrate the effectiveness and robustness of ORAT in handling outliers and adversarial attacks. Our code is available at https://github.com/discovershu/ORAT.

Fairness-aware Differentially Private Collaborative Filtering

Recently, there has been an increasing adoption of differential privacy guided algorithms for privacy-preserving machine learning tasks. However, the use of such algorithms comes with trade-offs in terms of algorithmic fairness, which has been widely acknowledged. Specifically, we have empirically observed that the classical collaborative filtering method, trained by differentially private stochastic gradient descent (DP-SGD), results in a disparate impact on user groups with respect to different user engagement levels. This, in turn, causes the original unfair model to become even more biased against inactive users. To address the above issues, we propose \textbf{DP-Fair}, a two-stage framework for collaborative filtering based algorithms. Specifically, it combines differential privacy mechanisms with fairness constraints to protect user privacy while ensuring fair recommendations. The experimental results, based on Amazon datasets, and user history logs collected from Etsy, one of the largest e-commerce platforms, demonstrate that our proposed method exhibits superior performance in terms of both overall accuracy and user group fairness on both shallow and deep recommendation models compared to vanilla DP-SGD.

Minimax AUC Fairness: Efficient Algorithm with Provable Convergence

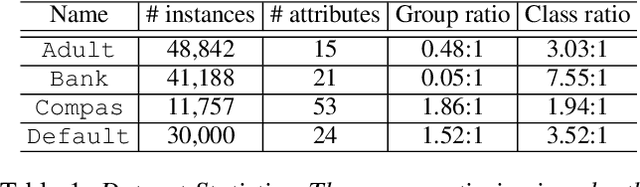
The use of machine learning models in consequential decision making often exacerbates societal inequity, in particular yielding disparate impact on members of marginalized groups defined by race and gender. The area under the ROC curve (AUC) is widely used to evaluate the performance of a scoring function in machine learning, but is studied in algorithmic fairness less than other performance metrics. Due to the pairwise nature of the AUC, defining an AUC-based group fairness metric is pairwise-dependent and may involve both \emph{intra-group} and \emph{inter-group} AUCs. Importantly, considering only one category of AUCs is not sufficient to mitigate unfairness in AUC optimization. In this paper, we propose a minimax learning and bias mitigation framework that incorporates both intra-group and inter-group AUCs while maintaining utility. Based on this Rawlsian framework, we design an efficient stochastic optimization algorithm and prove its convergence to the minimum group-level AUC. We conduct numerical experiments on both synthetic and real-world datasets to validate the effectiveness of the minimax framework and the proposed optimization algorithm.

Differentially Private SGDA for Minimax Problems

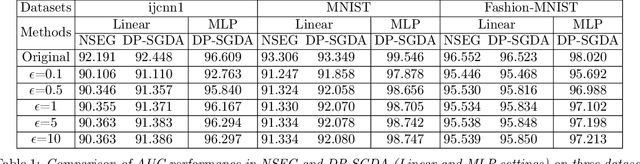
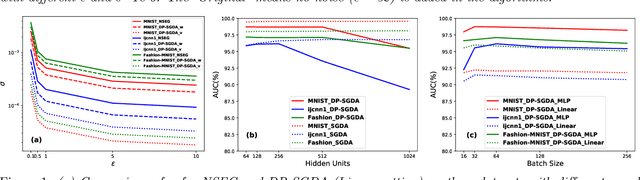
Stochastic gradient descent ascent (SGDA) and its variants have been the workhorse for solving minimax problems. However, in contrast to the well-studied stochastic gradient descent (SGD) with differential privacy (DP) constraints, there is little work on understanding the generalization (utility) of SGDA with DP constraints. In this paper, we use the algorithmic stability approach to establish the generalization (utility) of DP-SGDA in different settings. In particular, for the convex-concave setting, we prove that the DP-SGDA can achieve an optimal utility rate in terms of the weak primal-dual population risk in both smooth and non-smooth cases. To our best knowledge, this is the first-ever-known result for DP-SGDA in the non-smooth case. We further provide its utility analysis in the nonconvex-strongly-concave setting which is the first-ever-known result in terms of the primal population risk. The convergence and generalization results for this nonconvex setting are new even in the non-private setting. Finally, numerical experiments are conducted to demonstrate the effectiveness of DP-SGDA for both convex and nonconvex cases.

Simple Stochastic and Online Gradient Descent Algorithms for Pairwise Learning

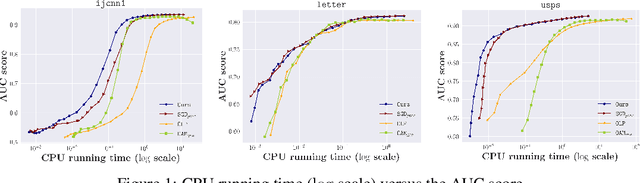
Pairwise learning refers to learning tasks where the loss function depends on a pair of instances. It instantiates many important machine learning tasks such as bipartite ranking and metric learning. A popular approach to handle streaming data in pairwise learning is an online gradient descent (OGD) algorithm, where one needs to pair the current instance with a buffering set of previous instances with a sufficiently large size and therefore suffers from a scalability issue. In this paper, we propose simple stochastic and online gradient descent methods for pairwise learning. A notable difference from the existing studies is that we only pair the current instance with the previous one in building a gradient direction, which is efficient in both the storage and computational complexity. We develop novel stability results, optimization, and generalization error bounds for both convex and nonconvex as well as both smooth and nonsmooth problems. We introduce novel techniques to decouple the dependency of models and the previous instance in both the optimization and generalization analysis. Our study resolves an open question on developing meaningful generalization bounds for OGD using a buffering set with a very small fixed size. We also extend our algorithms and stability analysis to develop differentially private SGD algorithms for pairwise learning which significantly improves the existing results.

Stability and Generalization of Stochastic Gradient Methods for Minimax Problems

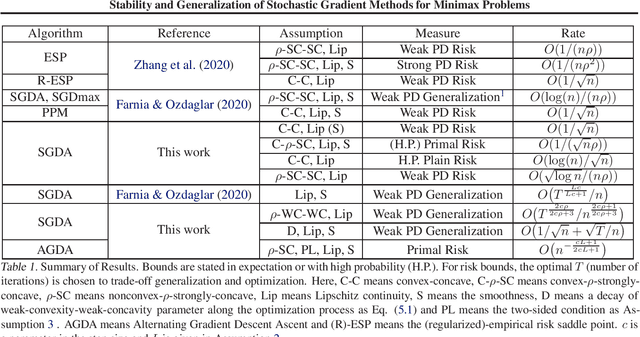
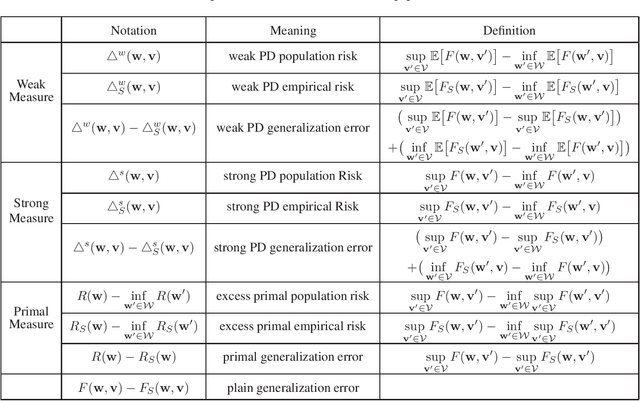
Many machine learning problems can be formulated as minimax problems such as Generative Adversarial Networks (GANs), AUC maximization and robust estimation, to mention but a few. A substantial amount of studies are devoted to studying the convergence behavior of their stochastic gradient-type algorithms. In contrast, there is relatively little work on their generalization, i.e., how the learning models built from training examples would behave on test examples. In this paper, we provide a comprehensive generalization analysis of stochastic gradient methods for minimax problems under both convex-concave and nonconvex-nonconcave cases through the lens of algorithmic stability. We establish a quantitative connection between stability and several generalization measures both in expectation and with high probability. For the convex-concave setting, our stability analysis shows that stochastic gradient descent ascent attains optimal generalization bounds for both smooth and nonsmooth minimax problems. We also establish generalization bounds for both weakly-convex-weakly-concave and gradient-dominated problems.

Stochastic Hard Thresholding Algorithms for AUC Maximization

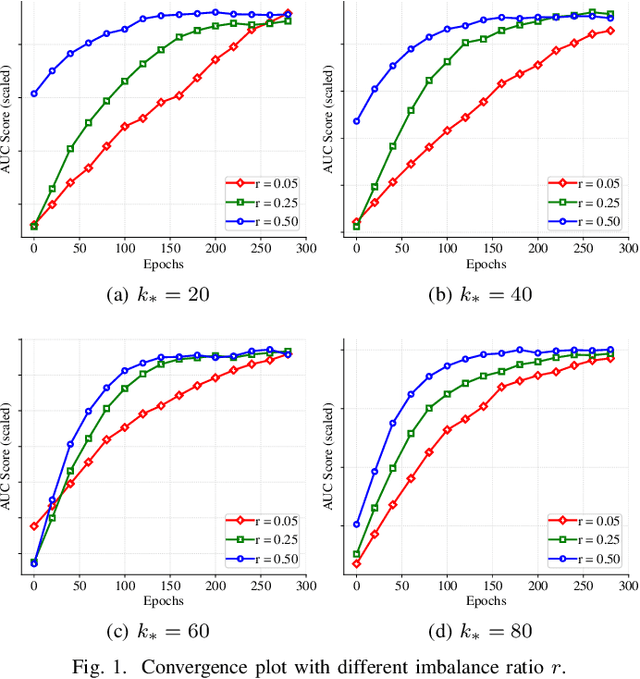
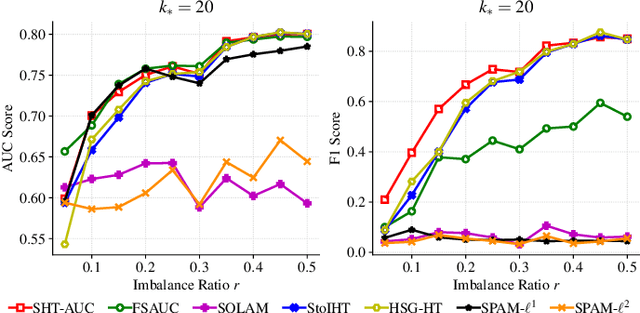
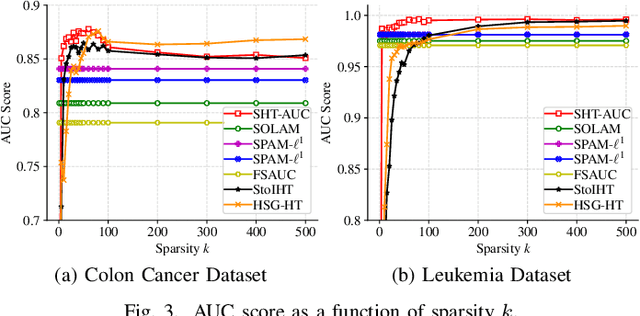
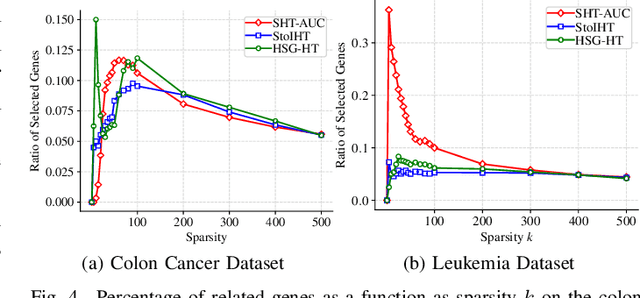
In this paper, we aim to develop stochastic hard thresholding algorithms for the important problem of AUC maximization in imbalanced classification. The main challenge is the pairwise loss involved in AUC maximization. We overcome this obstacle by reformulating the U-statistics objective function as an empirical risk minimization (ERM), from which a stochastic hard thresholding algorithm (\texttt{SHT-AUC}) is developed. To our best knowledge, this is the first attempt to provide stochastic hard thresholding algorithms for AUC maximization with a per-iteration cost $\O(b d)$ where $d$ and $b$ are the dimension of the data and the minibatch size, respectively. We show that the proposed algorithm enjoys the linear convergence rate up to a tolerance error. In particular, we show, if the data is generated from the Gaussian distribution, then its convergence becomes slower as the data gets more imbalanced. We conduct extensive experiments to show the efficiency and effectiveness of the proposed algorithms.

Stability and Optimization Error of Stochastic Gradient Descent for Pairwise Learning

In this paper we study the stability and its trade-off with optimization error for stochastic gradient descent (SGD) algorithms in the pairwise learning setting. Pairwise learning refers to a learning task which involves a loss function depending on pairs of instances among which notable examples are bipartite ranking, metric learning, area under ROC (AUC) maximization and minimum error entropy (MEE) principle. Our contribution is twofold. Firstly, we establish the stability results of SGD for pairwise learning in the convex, strongly convex and non-convex settings, from which generalization bounds can be naturally derived. Secondly, we establish the trade-off between stability and optimization error of SGD algorithms for pairwise learning. This is achieved by lower-bounding the sum of stability and optimization error by the minimax statistical error over a prescribed class of pairwise loss functions. From this fundamental trade-off, we obtain lower bounds for the optimization error of SGD algorithms and the excess expected risk over a class of pairwise losses. In addition, we illustrate our stability results by giving some specific examples of AUC maximization, metric learning and MEE.