Generalization analysis with deep ReLU networks for metric and similarity learning

While considerable theoretical progress has been devoted to the study of metric and similarity learning, the generalization mystery is still missing. In this paper, we study the generalization performance of metric and similarity learning by leveraging the specific structure of the true metric (the target function). Specifically, by deriving the explicit form of the true metric for metric and similarity learning with the hinge loss, we construct a structured deep ReLU neural network as an approximation of the true metric, whose approximation ability relies on the network complexity. Here, the network complexity corresponds to the depth, the number of nonzero weights and the computation units of the network. Consider the hypothesis space which consists of the structured deep ReLU networks, we develop the excess generalization error bounds for a metric and similarity learning problem by estimating the approximation error and the estimation error carefully. An optimal excess risk rate is derived by choosing the proper capacity of the constructed hypothesis space. To the best of our knowledge, this is the first-ever-known generalization analysis providing the excess generalization error for metric and similarity learning. In addition, we investigate the properties of the true metric of metric and similarity learning with general losses.

Generalization Guarantees of Gradient Descent for Multi-Layer Neural Networks

Recently, significant progress has been made in understanding the generalization of neural networks (NNs) trained by gradient descent (GD) using the algorithmic stability approach. However, most of the existing research has focused on one-hidden-layer NNs and has not addressed the impact of different network scaling parameters. In this paper, we greatly extend the previous work \cite{lei2022stability,richards2021stability} by conducting a comprehensive stability and generalization analysis of GD for multi-layer NNs. For two-layer NNs, our results are established under general network scaling parameters, relaxing previous conditions. In the case of three-layer NNs, our technical contribution lies in demonstrating its nearly co-coercive property by utilizing a novel induction strategy that thoroughly explores the effects of over-parameterization. As a direct application of our general findings, we derive the excess risk rate of $O(1/\sqrt{n})$ for GD algorithms in both two-layer and three-layer NNs. This sheds light on sufficient or necessary conditions for under-parameterized and over-parameterized NNs trained by GD to attain the desired risk rate of $O(1/\sqrt{n})$. Moreover, we demonstrate that as the scaling parameter increases or the network complexity decreases, less over-parameterization is required for GD to achieve the desired error rates. Additionally, under a low-noise condition, we obtain a fast risk rate of $O(1/n)$ for GD in both two-layer and three-layer NNs.

Stability and Generalization for Markov Chain Stochastic Gradient Methods

Recently there is a large amount of work devoted to the study of Markov chain stochastic gradient methods (MC-SGMs) which mainly focus on their convergence analysis for solving minimization problems. In this paper, we provide a comprehensive generalization analysis of MC-SGMs for both minimization and minimax problems through the lens of algorithmic stability in the framework of statistical learning theory. For empirical risk minimization (ERM) problems, we establish the optimal excess population risk bounds for both smooth and non-smooth cases by introducing on-average argument stability. For minimax problems, we develop a quantitative connection between on-average argument stability and generalization error which extends the existing results for uniform stability \cite{lei2021stability}. We further develop the first nearly optimal convergence rates for convex-concave problems both in expectation and with high probability, which, combined with our stability results, show that the optimal generalization bounds can be attained for both smooth and non-smooth cases. To the best of our knowledge, this is the first generalization analysis of SGMs when the gradients are sampled from a Markov process.

Differentially Private Stochastic Gradient Descent with Low-Noise

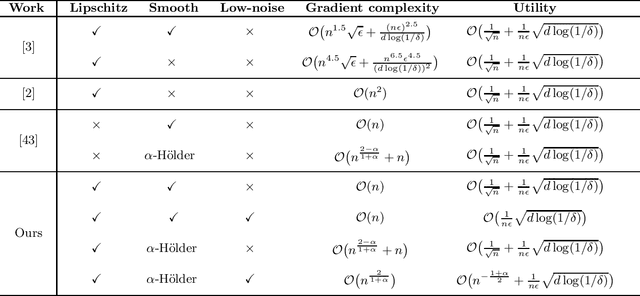
In this paper, by introducing a low-noise condition, we study privacy and utility (generalization) performances of differentially private stochastic gradient descent (SGD) algorithms in a setting of stochastic convex optimization (SCO) for both pointwise and pairwise learning problems. For pointwise learning, we establish sharper excess risk bounds of order $\mathcal{O}\Big( \frac{\sqrt{d\log(1/\delta)}}{n\epsilon} \Big)$ and $\mathcal{O}\Big( {n^{- \frac{1+\alpha}{2}}}+\frac{\sqrt{d\log(1/\delta)}}{n\epsilon}\Big)$ for the $(\epsilon,\delta)$-differentially private SGD algorithm for strongly smooth and $\alpha$-H\"older smooth losses, respectively, where $n$ is the sample size and $d$ is the dimensionality. For pairwise learning, inspired by \cite{lei2020sharper,lei2021generalization}, we propose a simple private SGD algorithm based on gradient perturbation which satisfies $(\epsilon,\delta)$-differential privacy, and develop novel utility bounds for the proposed algorithm. In particular, we prove that our algorithm can achieve excess risk rates $\mathcal{O}\Big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d\log(1/\delta)}}{n\epsilon}\Big)$ with gradient complexity $\mathcal{O}(n)$ and $\mathcal{O}\big(n^{\frac{2-\alpha}{1+\alpha}}+n\big)$ for strongly smooth and $\alpha$-H\"older smooth losses, respectively. Further, faster learning rates are established in a low-noise setting for both smooth and non-smooth losses. To the best of our knowledge, this is the first utility analysis which provides excess population bounds better than $\mathcal{O}\Big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d\log(1/\delta)}}{n\epsilon}\Big)$ for privacy-preserving pairwise learning.

Simple Stochastic and Online Gradient Descent Algorithms for Pairwise Learning

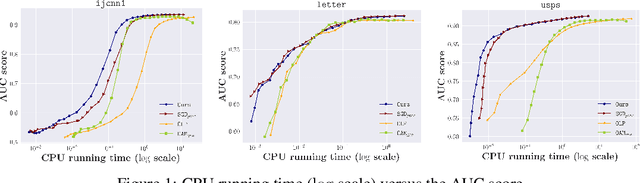
Pairwise learning refers to learning tasks where the loss function depends on a pair of instances. It instantiates many important machine learning tasks such as bipartite ranking and metric learning. A popular approach to handle streaming data in pairwise learning is an online gradient descent (OGD) algorithm, where one needs to pair the current instance with a buffering set of previous instances with a sufficiently large size and therefore suffers from a scalability issue. In this paper, we propose simple stochastic and online gradient descent methods for pairwise learning. A notable difference from the existing studies is that we only pair the current instance with the previous one in building a gradient direction, which is efficient in both the storage and computational complexity. We develop novel stability results, optimization, and generalization error bounds for both convex and nonconvex as well as both smooth and nonsmooth problems. We introduce novel techniques to decouple the dependency of models and the previous instance in both the optimization and generalization analysis. Our study resolves an open question on developing meaningful generalization bounds for OGD using a buffering set with a very small fixed size. We also extend our algorithms and stability analysis to develop differentially private SGD algorithms for pairwise learning which significantly improves the existing results.

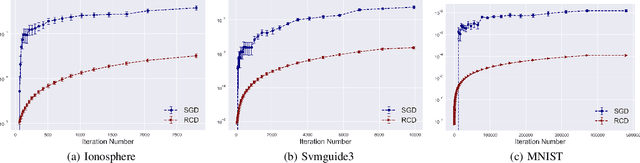
Stability and Generalization for Randomized Coordinate Descent

Randomized coordinate descent (RCD) is a popular optimization algorithm with wide applications in solving various machine learning problems, which motivates a lot of theoretical analysis on its convergence behavior. As a comparison, there is no work studying how the models trained by RCD would generalize to test examples. In this paper, we initialize the generalization analysis of RCD by leveraging the powerful tool of algorithmic stability. We establish argument stability bounds of RCD for both convex and strongly convex objectives, from which we develop optimal generalization bounds by showing how to early-stop the algorithm to tradeoff the estimation and optimization. Our analysis shows that RCD enjoys better stability as compared to stochastic gradient descent.

Differentially Private SGD with Non-Smooth Loss

In this paper, we are concerned with differentially private SGD algorithms in the setting of stochastic convex optimization (SCO). Most of existing work requires the loss to be Lipschitz continuous and strongly smooth, and the model parameter to be uniformly bounded. However, these assumptions are restrictive as many popular losses violate these conditions including the hinge loss for SVM, the absolute loss in robust regression, and even the least square loss in an unbounded domain. We significantly relax these restrictive assumptions and establish privacy and generalization (utility) guarantees for private SGD algorithms using output and gradient perturbations associated with non-smooth convex losses. Specifically, the loss function is relaxed to have $\alpha$-H\"{o}lder continuous gradient (referred to as $\alpha$-H\"{o}lder smoothness) which instantiates the Lipschitz continuity ($\alpha=0$) and strong smoothness ($\alpha=1$). We prove that noisy SGD with $\alpha$-H\"older smooth losses using gradient perturbation can guarantee $(\epsilon,\delta)$-differential privacy (DP) and attain optimal excess population risk $O\Big(\frac{\sqrt{d\log(1/\delta)}}{n\epsilon}+\frac{1}{\sqrt{n}}\Big)$, up to logarithmic terms, with gradient complexity (i.e. the total number of iterations) $T =O( n^{2-\alpha\over 1+\alpha}+ n).$ This shows an important trade-off between $\alpha$-H\"older smoothness of the loss and the computational complexity $T$ for private SGD with statistically optimal performance. In particular, our results indicate that $\alpha$-H\"older smoothness with $\alpha\ge {1/2}$ is sufficient to guarantee $(\epsilon,\delta)$-DP of noisy SGD algorithms while achieving optimal excess risk with linear gradient complexity $T = O(n).$

Differential Privacy for Sparse Classification Learning

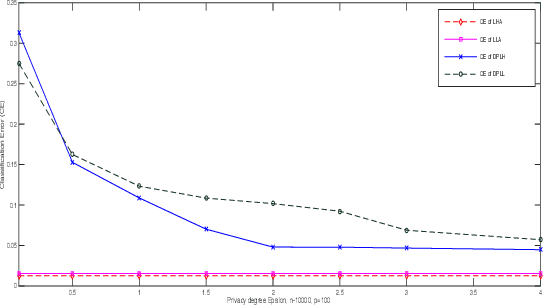
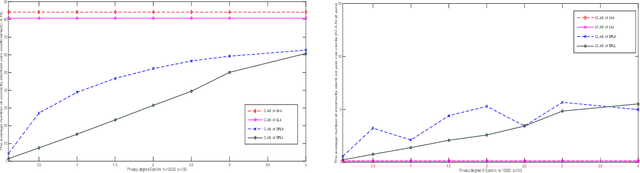
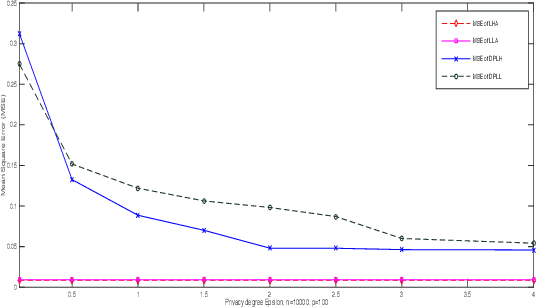
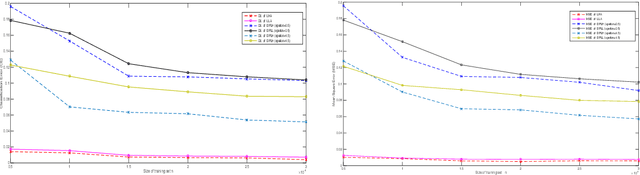
In this paper, we present a differential privacy version of convex and nonconvex sparse classification approach. Based on alternating direction method of multiplier (ADMM) algorithm, we transform the solving of sparse problem into the multistep iteration process. Then we add exponential noise to stable steps to achieve privacy protection. By the property of the post-processing holding of differential privacy, the proposed approach satisfies the $\epsilon-$differential privacy even when the original problem is unstable. Furthermore, we present the theoretical privacy bound of the differential privacy classification algorithm. Specifically, the privacy bound of our algorithm is controlled by the algorithm iteration number, the privacy parameter, the parameter of loss function, ADMM pre-selected parameter, and the data size. Finally we apply our framework to logistic regression with $L_1$ regularizer and logistic regression with $L_{1/2}$ regularizer. Numerical studies demonstrate that our method is both effective and efficient which performs well in sensitive data analysis.