On Discriminative Probabilistic Modeling for Self-Supervised Representation Learning

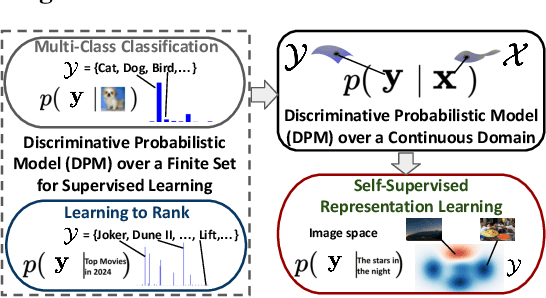
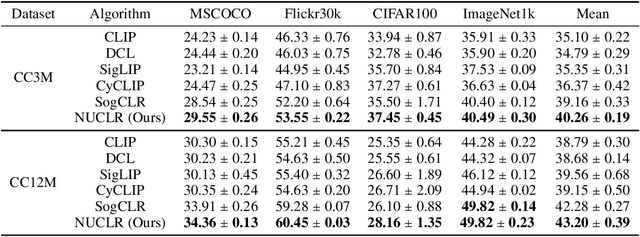
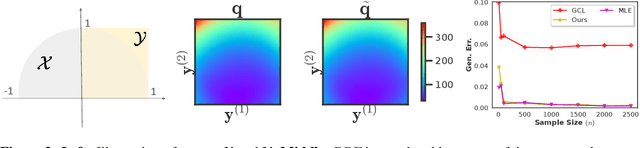
We study the discriminative probabilistic modeling problem on a continuous domain for (multimodal) self-supervised representation learning. To address the challenge of computing the integral in the partition function for each anchor data, we leverage the multiple importance sampling (MIS) technique for robust Monte Carlo integration, which can recover InfoNCE-based contrastive loss as a special case. Within this probabilistic modeling framework, we conduct generalization error analysis to reveal the limitation of current InfoNCE-based contrastive loss for self-supervised representation learning and derive insights for developing better approaches by reducing the error of Monte Carlo integration. To this end, we propose a novel non-parametric method for approximating the sum of conditional densities required by MIS through convex optimization, yielding a new contrastive objective for self-supervised representation learning. Moreover, we design an efficient algorithm for solving the proposed objective. We empirically compare our algorithm to representative baselines on the contrastive image-language pretraining task. Experimental results on the CC3M and CC12M datasets demonstrate the superior overall performance of our algorithm.

Differentially Private Non-convex Learning for Multi-layer Neural Networks

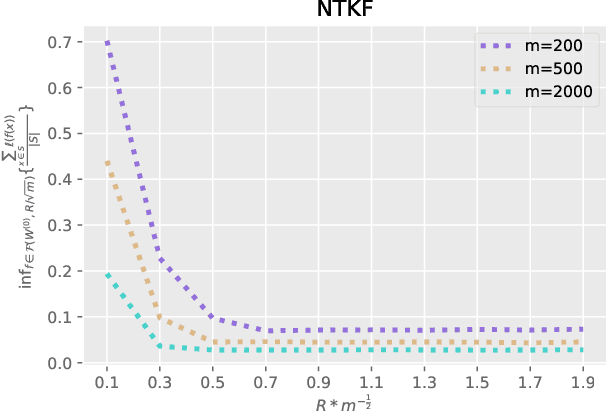
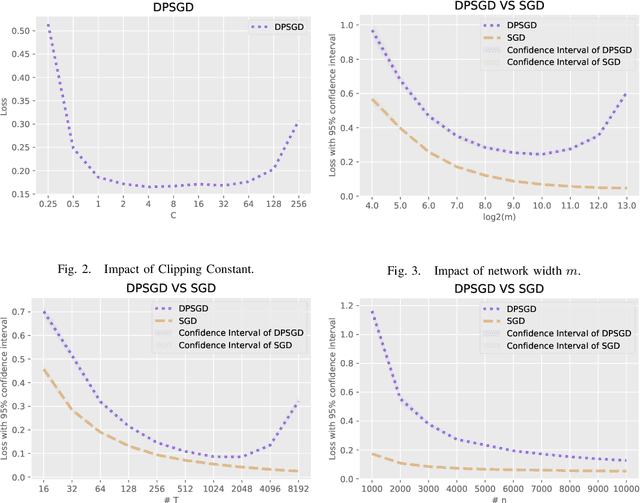
This paper focuses on the problem of Differentially Private Stochastic Optimization for (multi-layer) fully connected neural networks with a single output node. In the first part, we examine cases with no hidden nodes, specifically focusing on Generalized Linear Models (GLMs). We investigate the well-specific model where the random noise possesses a zero mean, and the link function is both bounded and Lipschitz continuous. We propose several algorithms and our analysis demonstrates the feasibility of achieving an excess population risk that remains invariant to the data dimension. We also delve into the scenario involving the ReLU link function, and our findings mirror those of the bounded link function. We conclude this section by contrasting well-specified and misspecified models, using ReLU regression as a representative example. In the second part of the paper, we extend our ideas to two-layer neural networks with sigmoid or ReLU activation functions in the well-specified model. In the third part, we study the theoretical guarantees of DP-SGD in Abadi et al. (2016) for fully connected multi-layer neural networks. By utilizing recent advances in Neural Tangent Kernel theory, we provide the first excess population risk when both the sample size and the width of the network are sufficiently large. Additionally, we discuss the role of some parameters in DP-SGD regarding their utility, both theoretically and empirically.

Outlier Robust Adversarial Training

Supervised learning models are challenged by the intrinsic complexities of training data such as outliers and minority subpopulations and intentional attacks at inference time with adversarial samples. While traditional robust learning methods and the recent adversarial training approaches are designed to handle each of the two challenges, to date, no work has been done to develop models that are robust with regard to the low-quality training data and the potential adversarial attack at inference time simultaneously. It is for this reason that we introduce Outlier Robust Adversarial Training (ORAT) in this work. ORAT is based on a bi-level optimization formulation of adversarial training with a robust rank-based loss function. Theoretically, we show that the learning objective of ORAT satisfies the $\mathcal{H}$-consistency in binary classification, which establishes it as a proper surrogate to adversarial 0/1 loss. Furthermore, we analyze its generalization ability and provide uniform convergence rates in high probability. ORAT can be optimized with a simple algorithm. Experimental evaluations on three benchmark datasets demonstrate the effectiveness and robustness of ORAT in handling outliers and adversarial attacks. Our code is available at https://github.com/discovershu/ORAT.

Stability and Generalization of Stochastic Compositional Gradient Descent Algorithms

Many machine learning tasks can be formulated as a stochastic compositional optimization (SCO) problem such as reinforcement learning, AUC maximization, and meta-learning, where the objective function involves a nested composition associated with an expectation. While a significant amount of studies has been devoted to studying the convergence behavior of SCO algorithms, there is little work on understanding their generalization, i.e., how these learning algorithms built from training examples would behave on future test examples. In this paper, we provide the stability and generalization analysis of stochastic compositional gradient descent algorithms through the lens of algorithmic stability in the framework of statistical learning theory. Firstly, we introduce a stability concept called compositional uniform stability and establish its quantitative relation with generalization for SCO problems. Then, we establish the compositional uniform stability results for two popular stochastic compositional gradient descent algorithms, namely SCGD and SCSC. Finally, we derive dimension-independent excess risk bounds for SCGD and SCSC by trade-offing their stability results and optimization errors. To the best of our knowledge, these are the first-ever-known results on stability and generalization analysis of stochastic compositional gradient descent algorithms.

Three-Way Trade-Off in Multi-Objective Learning: Optimization, Generalization and Conflict-Avoidance

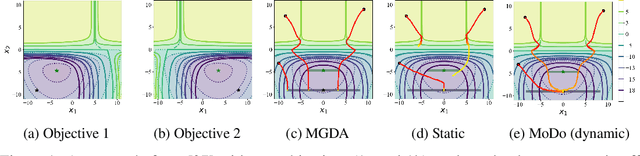
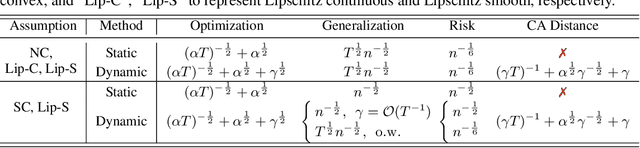
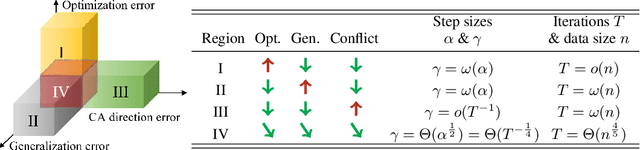
Multi-objective learning (MOL) problems often arise in emerging machine learning problems when there are multiple learning criteria or multiple learning tasks. Recent works have developed various dynamic weighting algorithms for MOL such as MGDA and its variants, where the central idea is to find an update direction that avoids conflicts among objectives. Albeit its appealing intuition, empirical studies show that dynamic weighting methods may not always outperform static ones. To understand this theory-practical gap, we focus on a new stochastic variant of MGDA - the Multi-objective gradient with Double sampling (MoDo) algorithm, and study the generalization performance of the dynamic weighting-based MoDo and its interplay with optimization through the lens of algorithm stability. Perhaps surprisingly, we find that the key rationale behind MGDA -- updating along conflict-avoidant direction - may hinder dynamic weighting algorithms from achieving the optimal ${\cal O}(1/\sqrt{n})$ population risk, where $n$ is the number of training samples. We further demonstrate the variability of dynamic weights on the three-way trade-off among optimization, generalization, and conflict avoidance that is unique in MOL.

Generalization Guarantees of Gradient Descent for Multi-Layer Neural Networks

Recently, significant progress has been made in understanding the generalization of neural networks (NNs) trained by gradient descent (GD) using the algorithmic stability approach. However, most of the existing research has focused on one-hidden-layer NNs and has not addressed the impact of different network scaling parameters. In this paper, we greatly extend the previous work \cite{lei2022stability,richards2021stability} by conducting a comprehensive stability and generalization analysis of GD for multi-layer NNs. For two-layer NNs, our results are established under general network scaling parameters, relaxing previous conditions. In the case of three-layer NNs, our technical contribution lies in demonstrating its nearly co-coercive property by utilizing a novel induction strategy that thoroughly explores the effects of over-parameterization. As a direct application of our general findings, we derive the excess risk rate of $O(1/\sqrt{n})$ for GD algorithms in both two-layer and three-layer NNs. This sheds light on sufficient or necessary conditions for under-parameterized and over-parameterized NNs trained by GD to attain the desired risk rate of $O(1/\sqrt{n})$. Moreover, we demonstrate that as the scaling parameter increases or the network complexity decreases, less over-parameterization is required for GD to achieve the desired error rates. Additionally, under a low-noise condition, we obtain a fast risk rate of $O(1/n)$ for GD in both two-layer and three-layer NNs.

Fairness-aware Differentially Private Collaborative Filtering

Recently, there has been an increasing adoption of differential privacy guided algorithms for privacy-preserving machine learning tasks. However, the use of such algorithms comes with trade-offs in terms of algorithmic fairness, which has been widely acknowledged. Specifically, we have empirically observed that the classical collaborative filtering method, trained by differentially private stochastic gradient descent (DP-SGD), results in a disparate impact on user groups with respect to different user engagement levels. This, in turn, causes the original unfair model to become even more biased against inactive users. To address the above issues, we propose \textbf{DP-Fair}, a two-stage framework for collaborative filtering based algorithms. Specifically, it combines differential privacy mechanisms with fairness constraints to protect user privacy while ensuring fair recommendations. The experimental results, based on Amazon datasets, and user history logs collected from Etsy, one of the largest e-commerce platforms, demonstrate that our proposed method exhibits superior performance in terms of both overall accuracy and user group fairness on both shallow and deep recommendation models compared to vanilla DP-SGD.

Generalization Analysis for Contrastive Representation Learning

Recently, contrastive learning has found impressive success in advancing the state of the art in solving various machine learning tasks. However, the existing generalization analysis is very limited or even not meaningful. In particular, the existing generalization error bounds depend linearly on the number $k$ of negative examples while it was widely shown in practice that choosing a large $k$ is necessary to guarantee good generalization of contrastive learning in downstream tasks. In this paper, we establish novel generalization bounds for contrastive learning which do not depend on $k$, up to logarithmic terms. Our analysis uses structural results on empirical covering numbers and Rademacher complexities to exploit the Lipschitz continuity of loss functions. For self-bounding Lipschitz loss functions, we further improve our results by developing optimistic bounds which imply fast rates in a low noise condition. We apply our results to learning with both linear representation and nonlinear representation by deep neural networks, for both of which we derive Rademacher complexity bounds to get improved generalization bounds.

Stability and Generalization Analysis of Gradient Methods for Shallow Neural Networks

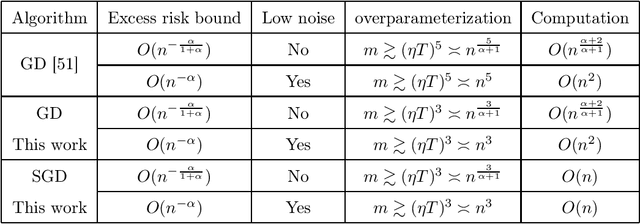
While significant theoretical progress has been achieved, unveiling the generalization mystery of overparameterized neural networks still remains largely elusive. In this paper, we study the generalization behavior of shallow neural networks (SNNs) by leveraging the concept of algorithmic stability. We consider gradient descent (GD) and stochastic gradient descent (SGD) to train SNNs, for both of which we develop consistent excess risk bounds by balancing the optimization and generalization via early-stopping. As compared to existing analysis on GD, our new analysis requires a relaxed overparameterization assumption and also applies to SGD. The key for the improvement is a better estimation of the smallest eigenvalues of the Hessian matrices of the empirical risks and the loss function along the trajectories of GD and SGD by providing a refined estimation of their iterates.

Stability and Generalization for Markov Chain Stochastic Gradient Methods

Recently there is a large amount of work devoted to the study of Markov chain stochastic gradient methods (MC-SGMs) which mainly focus on their convergence analysis for solving minimization problems. In this paper, we provide a comprehensive generalization analysis of MC-SGMs for both minimization and minimax problems through the lens of algorithmic stability in the framework of statistical learning theory. For empirical risk minimization (ERM) problems, we establish the optimal excess population risk bounds for both smooth and non-smooth cases by introducing on-average argument stability. For minimax problems, we develop a quantitative connection between on-average argument stability and generalization error which extends the existing results for uniform stability \cite{lei2021stability}. We further develop the first nearly optimal convergence rates for convex-concave problems both in expectation and with high probability, which, combined with our stability results, show that the optimal generalization bounds can be attained for both smooth and non-smooth cases. To the best of our knowledge, this is the first generalization analysis of SGMs when the gradients are sampled from a Markov process.