Three-Way Trade-Off in Multi-Objective Learning: Optimization, Generalization and Conflict-Avoidance
Paper and Code
May 31, 2023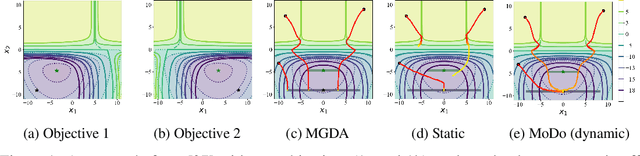
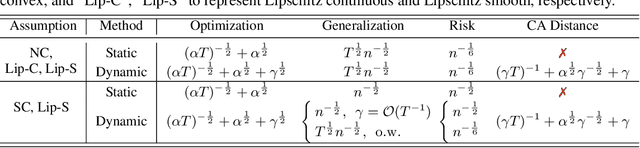
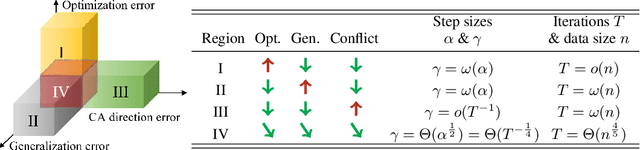

Multi-objective learning (MOL) problems often arise in emerging machine learning problems when there are multiple learning criteria or multiple learning tasks. Recent works have developed various dynamic weighting algorithms for MOL such as MGDA and its variants, where the central idea is to find an update direction that avoids conflicts among objectives. Albeit its appealing intuition, empirical studies show that dynamic weighting methods may not always outperform static ones. To understand this theory-practical gap, we focus on a new stochastic variant of MGDA - the Multi-objective gradient with Double sampling (MoDo) algorithm, and study the generalization performance of the dynamic weighting-based MoDo and its interplay with optimization through the lens of algorithm stability. Perhaps surprisingly, we find that the key rationale behind MGDA -- updating along conflict-avoidant direction - may hinder dynamic weighting algorithms from achieving the optimal ${\cal O}(1/\sqrt{n})$ population risk, where $n$ is the number of training samples. We further demonstrate the variability of dynamic weights on the three-way trade-off among optimization, generalization, and conflict avoidance that is unique in MOL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge