Stability and Generalization Analysis of Gradient Methods for Shallow Neural Networks
Paper and Code
Sep 19, 2022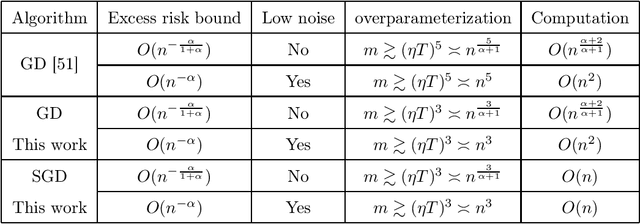
While significant theoretical progress has been achieved, unveiling the generalization mystery of overparameterized neural networks still remains largely elusive. In this paper, we study the generalization behavior of shallow neural networks (SNNs) by leveraging the concept of algorithmic stability. We consider gradient descent (GD) and stochastic gradient descent (SGD) to train SNNs, for both of which we develop consistent excess risk bounds by balancing the optimization and generalization via early-stopping. As compared to existing analysis on GD, our new analysis requires a relaxed overparameterization assumption and also applies to SGD. The key for the improvement is a better estimation of the smallest eigenvalues of the Hessian matrices of the empirical risks and the loss function along the trajectories of GD and SGD by providing a refined estimation of their iterates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge