Differentially Private Stochastic Gradient Descent with Low-Noise
Paper and Code
Sep 09, 2022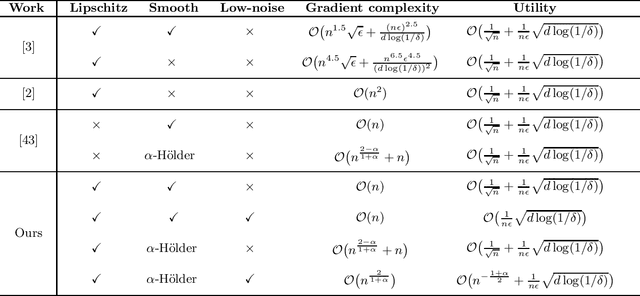

In this paper, by introducing a low-noise condition, we study privacy and utility (generalization) performances of differentially private stochastic gradient descent (SGD) algorithms in a setting of stochastic convex optimization (SCO) for both pointwise and pairwise learning problems. For pointwise learning, we establish sharper excess risk bounds of order $\mathcal{O}\Big( \frac{\sqrt{d\log(1/\delta)}}{n\epsilon} \Big)$ and $\mathcal{O}\Big( {n^{- \frac{1+\alpha}{2}}}+\frac{\sqrt{d\log(1/\delta)}}{n\epsilon}\Big)$ for the $(\epsilon,\delta)$-differentially private SGD algorithm for strongly smooth and $\alpha$-H\"older smooth losses, respectively, where $n$ is the sample size and $d$ is the dimensionality. For pairwise learning, inspired by \cite{lei2020sharper,lei2021generalization}, we propose a simple private SGD algorithm based on gradient perturbation which satisfies $(\epsilon,\delta)$-differential privacy, and develop novel utility bounds for the proposed algorithm. In particular, we prove that our algorithm can achieve excess risk rates $\mathcal{O}\Big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d\log(1/\delta)}}{n\epsilon}\Big)$ with gradient complexity $\mathcal{O}(n)$ and $\mathcal{O}\big(n^{\frac{2-\alpha}{1+\alpha}}+n\big)$ for strongly smooth and $\alpha$-H\"older smooth losses, respectively. Further, faster learning rates are established in a low-noise setting for both smooth and non-smooth losses. To the best of our knowledge, this is the first utility analysis which provides excess population bounds better than $\mathcal{O}\Big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d\log(1/\delta)}}{n\epsilon}\Big)$ for privacy-preserving pairwise learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge