Stochastic Gradient Descent with Momentum is Algorithmically Stable

Stochastic gradient descent with momentum (SGDM) is one of the most widely used optimization algorithms in machine learning. While optimization properties of SGDM have been extensively studied in the literature, it remains insufficiently understood whether and when SGDM can generalize well to unseen data. In particular, it has been conjectured that while momentum accelerates training, it may degrade generalization. In this paper, we close this gap by developing a comprehensive generalization analysis of SGDM through the lens of algorithmic stability. More specifically, we introduce a generalized SGDM framework that encompasses both Polyak's and Nesterov's momentum schemes, and establish tight on-average model stability bounds for smooth and convex problems. Notably, the obtained bounds exploit small optimization error bounds along the trajectory, apply to any momentum parameter in the interval $[0, 1)$, and do not require the commonly assumed Lipschitzness of loss functions. We further derive optimization error bounds for the generalized SGDM, and combine them with our generalization analyses to obtain optimal excess population risk bounds for SGDM with both Polyak's and Nesterov's momentum.

Learning Theory of the SVRG: Generalization and Convergence Analysis

Variance reduction (VR) methods employ stochastic gradients with decreasing variance, and they have been widely applied to solve large-scale optimization problems in machine learning because of their efficiency. Existing theoretical studies of VR methods are mainly focused on the convergence analysis, leaving the generalization behavior largely unexplored. In this paper, we bridge this gap by developing the first non-vacuous generalization analysis of the representative VR method: Stochastic Variance Reduced Gradient (SVRG), through the lens of algorithmic stability. In particular, we establish sharp stability bounds of the SVRG in both convex and strongly convex settings by exploiting its algorithmic structure. The obtained bounds are data-dependent, because the training errors are incorporated along the trajectory. Our analysis clarifies the interplay between optimization and generalization, leading to optimal excess population risk bounds in both settings. Our approach differs substantially from existing analyses of stochastic algorithms in the sense that we decompose the SVRG update as an SGD-like step plus a zero-mean correction term and then introduce novel Lyapunov functions to absorb the additional gradient terms induced by the reference points. Our analytical framework can be generalized to other VR methods, and we demonstrate the generalization by the well-known Stochastic Average Gradient Accelerated (SAGA) method.

Learning to Control: The iUzawa-Net for Nonsmooth Optimal Control of Linear PDEs

We propose an optimization-informed deep neural network approach, named iUzawa-Net, aiming for the first solver that enables real-time solutions for a class of nonsmooth optimal control problems of linear partial differential equations (PDEs). The iUzawa-Net unrolls an inexact Uzawa method for saddle point problems, replacing classical preconditioners and PDE solvers with specifically designed learnable neural networks. We prove universal approximation properties and establish the asymptotic $\varepsilon$-optimality for the iUzawa-Net, and validate its promising numerical efficiency through nonsmooth elliptic and parabolic optimal control problems. Our techniques offer a versatile framework for designing and analyzing various optimization-informed deep learning approaches to optimal control and other PDE-constrained optimization problems. The proposed learning-to-control approach synergizes model-based optimization algorithms and data-driven deep learning techniques, inheriting the merits of both methodologies.

Stability and Generalization of Nonconvex Optimization with Heavy-Tailed Noise

The empirical evidence indicates that stochastic optimization with heavy-tailed gradient noise is more appropriate to characterize the training of machine learning models than that with standard bounded gradient variance noise. Most existing works on this phenomenon focus on the convergence of optimization errors, while the analysis for generalization bounds under the heavy-tailed gradient noise remains limited. In this paper, we develop a general framework for establishing generalization bounds under heavy-tailed noise. Specifically, we introduce a truncation argument to achieve the generalization error bound based on the algorithmic stability under the assumption of bounded $p$th centered moment with $p\in(1,2]$. Building on this framework, we further provide the stability and generalization analysis for several popular stochastic algorithms under heavy-tailed noise, including clipped and normalized stochastic gradient descent, as well as their mini-batch and momentum variants.

BestServe: Serving Strategies with Optimal Goodput in Collocation and Disaggregation Architectures

Serving large language models (LLMs) to millions of users requires efficient resource allocation and parallelism strategies. It is a labor intensive trial-and-error process to find such a strategy. We present BestServe, a novel framework for ranking serving strategies by estimating goodput under various operating scenarios. Supporting both collocated and disaggregated architectures, BestServe leverages an inference simulator built on an adapted roofline model and CPU-GPU dispatch dynamics. Our framework determines the optimal strategy in minutes on a single standard CPU, eliminating the need for costly benchmarking, while achieving predictions within a $20\%$ error margin. It appeals to be practical for rapid deployment planning because of its lightweight design and strong extensibility.

SPAP: Structured Pruning via Alternating Optimization and Penalty Methods

The deployment of large language models (LLMs) is often constrained by their substantial computational and memory demands. While structured pruning presents a viable approach by eliminating entire network components, existing methods suffer from performance degradation, reliance on heuristic metrics, or expensive finetuning. To address these challenges, we propose SPAP (Structured Pruning via Alternating Optimization and Penalty Methods), a novel and efficient structured pruning framework for LLMs grounded in optimization theory. SPAP formulates the pruning problem through a mixed-integer optimization model, employs a penalty method that effectively makes pruning decisions to minimize pruning errors, and introduces an alternating minimization algorithm tailored to the splittable problem structure for efficient weight updates and performance recovery. Extensive experiments on OPT, LLaMA-3/3.1/3.2, and Qwen2.5 models demonstrate SPAP's superiority over state-of-the-art methods, delivering linear inference speedups (1.29$\times$ at 30% sparsity) and proportional memory reductions. Our work offers a practical, optimization-driven solution for pruning LLMs while preserving model performance.

FASP: Fast and Accurate Structured Pruning of Large Language Models

The rapid increase in the size of large language models (LLMs) has significantly escalated their computational and memory demands, posing challenges for efficient deployment, especially on resource-constrained devices. Structured pruning has emerged as an effective model compression method that can reduce these demands while preserving performance. In this paper, we introduce FASP (Fast and Accurate Structured Pruning), a novel structured pruning framework for LLMs that emphasizes both speed and accuracy. FASP employs a distinctive pruning structure that interlinks sequential layers, allowing for the removal of columns in one layer while simultaneously eliminating corresponding rows in the preceding layer without incurring additional performance loss. The pruning metric, inspired by Wanda, is computationally efficient and effectively selects components to prune. Additionally, we propose a restoration mechanism that enhances model fidelity by adjusting the remaining weights post-pruning. We evaluate FASP on the OPT and LLaMA model families, demonstrating superior performance in terms of perplexity and accuracy on downstream tasks compared to state-of-the-art methods. Our approach achieves significant speed-ups, pruning models such as OPT-125M in 17 seconds and LLaMA-30B in 15 minutes on a single NVIDIA RTX 4090 GPU, making it a highly practical solution for optimizing LLMs.

A Convex-optimization-based Layer-wise Post-training Pruner for Large Language Models

Pruning is a critical strategy for compressing trained large language models (LLMs), aiming at substantial memory conservation and computational acceleration without compromising performance. However, existing pruning methods often necessitate inefficient retraining for billion-scale LLMs or rely on heuristic methods such as the optimal brain surgeon framework, which degrade performance. In this paper, we introduce FISTAPruner, the first post-training pruner based on convex optimization models and algorithms. Specifically, we propose a convex optimization model incorporating $\ell_1$ norm to induce sparsity and utilize the FISTA solver for optimization. FISTAPruner incorporates an intra-layer cumulative error correction mechanism and supports parallel pruning. We comprehensively evaluate FISTAPruner on models such as OPT, LLaMA, LLaMA-2, and LLaMA-3 with 125M to 70B parameters under unstructured and 2:4 semi-structured sparsity, demonstrating superior performance over existing state-of-the-art methods across various language benchmarks.

Adapprox: Adaptive Approximation in Adam Optimization via Randomized Low-Rank Matrices

As deep learning models exponentially increase in size, optimizers such as Adam encounter significant memory consumption challenges due to the storage of first and second moment data. Current memory-efficient methods like Adafactor and CAME often compromise accuracy with their matrix factorization techniques. Addressing this, we introduce Adapprox, a novel approach that employs randomized low-rank matrix approximation for a more effective and accurate approximation of Adam's second moment. Adapprox features an adaptive rank selection mechanism, finely balancing accuracy and memory efficiency, and includes an optional cosine similarity guidance strategy to enhance stability and expedite convergence. In GPT-2 training and downstream tasks, Adapprox surpasses AdamW by achieving 34.5% to 49.9% and 33.8% to 49.9% memory savings for the 117M and 345M models, respectively, with the first moment enabled, and further increases these savings without the first moment. Besides, it enhances convergence speed and improves downstream task performance relative to its counterparts.

Coverage Axis++: Efficient Inner Point Selection for 3D Shape Skeletonization

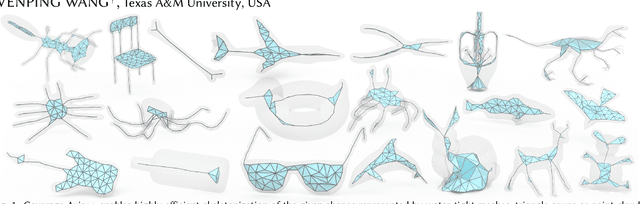
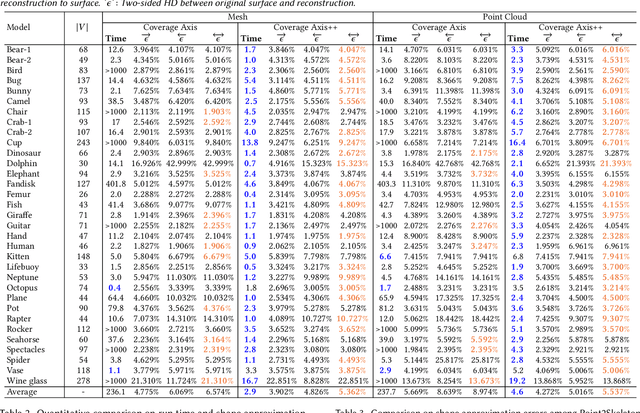
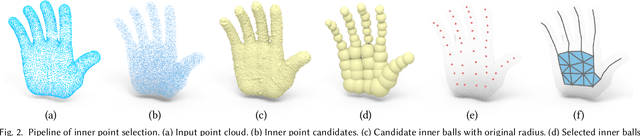
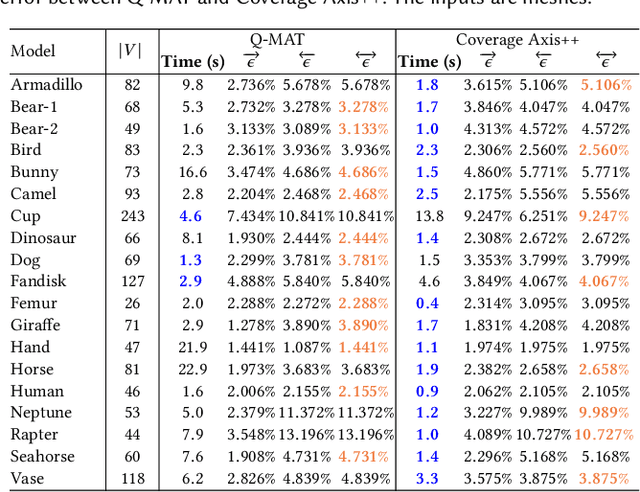
We introduce Coverage Axis++, a novel and efficient approach to 3D shape skeletonization. The current state-of-the-art approaches for this task often rely on the watertightness of the input or suffer from substantial computational costs, thereby limiting their practicality. To address this challenge, Coverage Axis++ proposes a heuristic algorithm to select skeletal points, offering a high-accuracy approximation of the Medial Axis Transform (MAT) while significantly mitigating computational intensity for various shape representations. We introduce a simple yet effective strategy that considers both shape coverage and uniformity to derive skeletal points. The selection procedure enforces consistency with the shape structure while favoring the dominant medial balls, which thus introduces a compact underlying shape representation in terms of MAT. As a result, Coverage Axis++ allows for skeletonization for various shape representations (e.g., water-tight meshes, triangle soups, point clouds), specification of the number of skeletal points, few hyperparameters, and highly efficient computation with improved reconstruction accuracy. Extensive experiments across a wide range of 3D shapes validate the efficiency and effectiveness of Coverage Axis++. The code will be publicly available once the paper is published.