SuperGaussians: Enhancing Gaussian Splatting Using Primitives with Spatially Varying Colors

Gaussian Splattings demonstrate impressive results in multi-view reconstruction based on Gaussian explicit representations. However, the current Gaussian primitives only have a single view-dependent color and an opacity to represent the appearance and geometry of the scene, resulting in a non-compact representation. In this paper, we introduce a new method called SuperGaussians that utilizes spatially varying colors and opacity in a single Gaussian primitive to improve its representation ability. We have implemented bilinear interpolation, movable kernels, and even tiny neural networks as spatially varying functions. Quantitative and qualitative experimental results demonstrate that all three functions outperform the baseline, with the best movable kernels achieving superior novel view synthesis performance on multiple datasets, highlighting the strong potential of spatially varying functions.

NASM: Neural Anisotropic Surface Meshing

This paper introduces a new learning-based method, NASM, for anisotropic surface meshing. Our key idea is to propose a graph neural network to embed an input mesh into a high-dimensional (high-d) Euclidean embedding space to preserve curvature-based anisotropic metric by using a dot product loss between high-d edge vectors. This can dramatically reduce the computational time and increase the scalability. Then, we propose a novel feature-sensitive remeshing on the generated high-d embedding to automatically capture sharp geometric features. We define a high-d normal metric, and then derive an automatic differentiation on a high-d centroidal Voronoi tessellation (CVT) optimization with the normal metric to simultaneously preserve geometric features and curvature anisotropy that exhibit in the original 3D shapes. To our knowledge, this is the first time that a deep learning framework and a large dataset are proposed to construct a high-d Euclidean embedding space for 3D anisotropic surface meshing. Experimental results are evaluated and compared with the state-of-the-art in anisotropic surface meshing on a large number of surface models from Thingi10K dataset as well as tested on extensive unseen 3D shapes from Multi-Garment Network dataset and FAUST human dataset.

Quasi-Medial Distance Field (Q-MDF): A Robust Method for Approximating and Discretizing Neural Medial Axis

The medial axis, a lower-dimensional shape descriptor, plays an important role in the field of digital geometry processing. Despite its importance, robust computation of the medial axis transform from diverse inputs, especially point clouds with defects, remains a significant challenge. In this paper, we tackle the challenge by proposing a new implicit method that diverges from mainstream explicit medial axis computation techniques. Our key technical insight is the difference between the signed distance field (SDF) and the medial field (MF) of a solid shape is the unsigned distance field (UDF) of the shape's medial axis. This allows for formulating medial axis computation as an implicit reconstruction problem. Utilizing a modified double covering method, we extract the medial axis as the zero level-set of the UDF. Extensive experiments show that our method has enhanced accuracy and robustness in learning compact medial axis transform from thorny meshes and point clouds compared to existing methods.

Correspondence-Free Non-Rigid Point Set Registration Using Unsupervised Clustering Analysis

This paper presents a novel non-rigid point set registration method that is inspired by unsupervised clustering analysis. Unlike previous approaches that treat the source and target point sets as separate entities, we develop a holistic framework where they are formulated as clustering centroids and clustering members, separately. We then adopt Tikhonov regularization with an $\ell_1$-induced Laplacian kernel instead of the commonly used Gaussian kernel to ensure smooth and more robust displacement fields. Our formulation delivers closed-form solutions, theoretical guarantees, independence from dimensions, and the ability to handle large deformations. Subsequently, we introduce a clustering-improved Nystr\"om method to effectively reduce the computational complexity and storage of the Gram matrix to linear, while providing a rigorous bound for the low-rank approximation. Our method achieves high accuracy results across various scenarios and surpasses competitors by a significant margin, particularly on shapes with substantial deformations. Additionally, we demonstrate the versatility of our method in challenging tasks such as shape transfer and medical registration.

Deep-PE: A Learning-Based Pose Evaluator for Point Cloud Registration

In the realm of point cloud registration, the most prevalent pose evaluation approaches are statistics-based, identifying the optimal transformation by maximizing the number of consistent correspondences. However, registration recall decreases significantly when point clouds exhibit a low overlap rate, despite efforts in designing feature descriptors and establishing correspondences. In this paper, we introduce Deep-PE, a lightweight, learning-based pose evaluator designed to enhance the accuracy of pose selection, especially in challenging point cloud scenarios with low overlap. Our network incorporates a Pose-Aware Attention (PAA) module to simulate and learn the alignment status of point clouds under various candidate poses, alongside a Pose Confidence Prediction (PCP) module that predicts the likelihood of successful registration. These two modules facilitate the learning of both local and global alignment priors. Extensive tests across multiple benchmarks confirm the effectiveness of Deep-PE. Notably, on 3DLoMatch with a low overlap rate, Deep-PE significantly outperforms state-of-the-art methods by at least 8% and 11% in registration recall under handcrafted FPFH and learning-based FCGF descriptors, respectively. To the best of our knowledge, this is the first study to utilize deep learning to select the optimal pose without the explicit need for input correspondences.

NeurCross: A Self-Supervised Neural Approach for Representing Cross Fields in Quad Mesh Generation

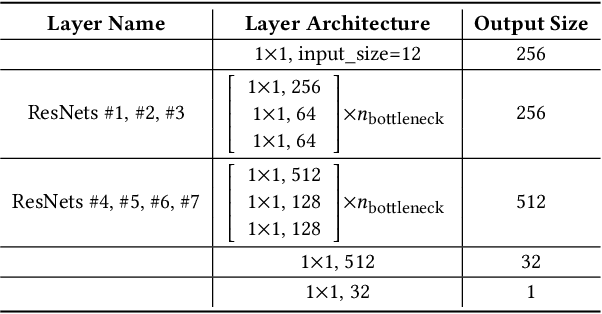
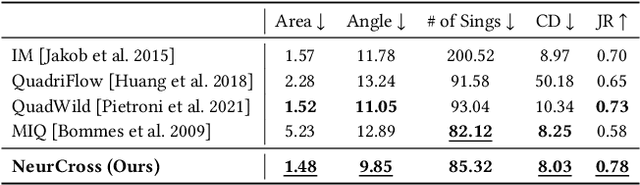
Quadrilateral mesh generation plays a crucial role in numerical simulations within Computer-Aided Design and Engineering (CAD/E). The quality of the cross field is essential for generating a quadrilateral mesh. In this paper, we propose a self-supervised neural representation of the cross field, named NeurCross, comprising two modules: one to fit the signed distance function (SDF) and another to predict the cross field. Unlike most existing approaches that operate directly on the given polygonal surface, NeurCross takes the SDF as a bridge to allow for SDF overfitting and the prediction of the cross field to proceed simultaneously. By utilizing a neural SDF, we achieve a smooth representation of the base surface, minimizing the impact of piecewise planar discretization and minor surface variations. Moreover, the principal curvatures and directions are fully encoded by the Hessian of the SDF, enabling the regularization of the overall cross field through minor adjustments to the SDF. Compared to state-of-the-art methods, NeurCross significantly improves the placement of singular points and the approximation accuracy between the input triangular surface and the output quad mesh, as demonstrated in the teaser figure.

ComboStoc: Combinatorial Stochasticity for Diffusion Generative Models

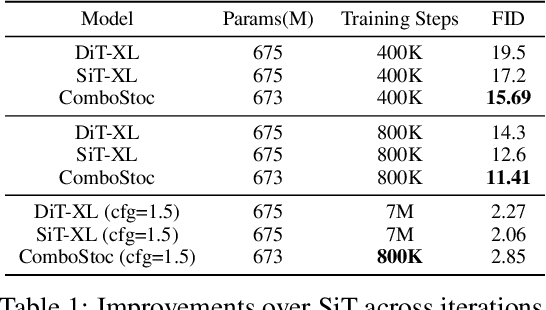
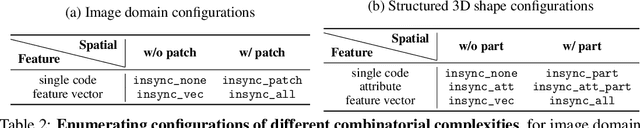
In this paper, we study an under-explored but important factor of diffusion generative models, i.e., the combinatorial complexity. Data samples are generally high-dimensional, and for various structured generation tasks, there are additional attributes which are combined to associate with data samples. We show that the space spanned by the combination of dimensions and attributes is insufficiently sampled by existing training scheme of diffusion generative models, causing degraded test time performance. We present a simple fix to this problem by constructing stochastic processes that fully exploit the combinatorial structures, hence the name ComboStoc. Using this simple strategy, we show that network training is significantly accelerated across diverse data modalities, including images and 3D structured shapes. Moreover, ComboStoc enables a new way of test time generation which uses insynchronized time steps for different dimensions and attributes, thus allowing for varying degrees of control over them.

CWF: Consolidating Weak Features in High-quality Mesh Simplification

In mesh simplification, common requirements like accuracy, triangle quality, and feature alignment are often considered as a trade-off. Existing algorithms concentrate on just one or a few specific aspects of these requirements. For example, the well-known Quadric Error Metrics (QEM) approach prioritizes accuracy and can preserve strong feature lines/points as well but falls short in ensuring high triangle quality and may degrade weak features that are not as distinctive as strong ones. In this paper, we propose a smooth functional that simultaneously considers all of these requirements. The functional comprises a normal anisotropy term and a Centroidal Voronoi Tessellation (CVT) energy term, with the variables being a set of movable points lying on the surface. The former inherits the spirit of QEM but operates in a continuous setting, while the latter encourages even point distribution, allowing various surface metrics. We further introduce a decaying weight to automatically balance the two terms. We selected 100 CAD models from the ABC dataset, along with 21 organic models, to compare the existing mesh simplification algorithms with ours. Experimental results reveal an important observation: the introduction of a decaying weight effectively reduces the conflict between the two terms and enables the alignment of weak features. This distinctive feature sets our approach apart from most existing mesh simplification methods and demonstrates significant potential in shape understanding.

NeurCADRecon: Neural Representation for Reconstructing CAD Surfaces by Enforcing Zero Gaussian Curvature

Despite recent advances in reconstructing an organic model with the neural signed distance function (SDF), the high-fidelity reconstruction of a CAD model directly from low-quality unoriented point clouds remains a significant challenge. In this paper, we address this challenge based on the prior observation that the surface of a CAD model is generally composed of piecewise surface patches, each approximately developable even around the feature line. Our approach, named NeurCADRecon, is self-supervised, and its loss includes a developability term to encourage the Gaussian curvature toward 0 while ensuring fidelity to the input points. Noticing that the Gaussian curvature is non-zero at tip points, we introduce a double-trough curve to tolerate the existence of these tip points. Furthermore, we develop a dynamic sampling strategy to deal with situations where the given points are incomplete or too sparse. Since our resulting neural SDFs can clearly manifest sharp feature points/lines, one can easily extract the feature-aligned triangle mesh from the SDF and then decompose it into smooth surface patches, greatly reducing the difficulty of recovering the parametric CAD design. A comprehensive comparison with existing state-of-the-art methods shows the significant advantage of our approach in reconstructing faithful CAD shapes.

Coverage Axis++: Efficient Inner Point Selection for 3D Shape Skeletonization

We introduce Coverage Axis++, a novel and efficient approach to 3D shape skeletonization. The current state-of-the-art approaches for this task often rely on the watertightness of the input or suffer from substantial computational costs, thereby limiting their practicality. To address this challenge, Coverage Axis++ proposes a heuristic algorithm to select skeletal points, offering a high-accuracy approximation of the Medial Axis Transform (MAT) while significantly mitigating computational intensity for various shape representations. We introduce a simple yet effective strategy that considers both shape coverage and uniformity to derive skeletal points. The selection procedure enforces consistency with the shape structure while favoring the dominant medial balls, which thus introduces a compact underlying shape representation in terms of MAT. As a result, Coverage Axis++ allows for skeletonization for various shape representations (e.g., water-tight meshes, triangle soups, point clouds), specification of the number of skeletal points, few hyperparameters, and highly efficient computation with improved reconstruction accuracy. Extensive experiments across a wide range of 3D shapes validate the efficiency and effectiveness of Coverage Axis++. The code will be publicly available once the paper is published.