Towards Unifying Understanding and Generation in the Era of Vision Foundation Models: A Survey from the Autoregression Perspective

Autoregression in large language models (LLMs) has shown impressive scalability by unifying all language tasks into the next token prediction paradigm. Recently, there is a growing interest in extending this success to vision foundation models. In this survey, we review the recent advances and discuss future directions for autoregressive vision foundation models. First, we present the trend for next generation of vision foundation models, i.e., unifying both understanding and generation in vision tasks. We then analyze the limitations of existing vision foundation models, and present a formal definition of autoregression with its advantages. Later, we categorize autoregressive vision foundation models from their vision tokenizers and autoregression backbones. Finally, we discuss several promising research challenges and directions. To the best of our knowledge, this is the first survey to comprehensively summarize autoregressive vision foundation models under the trend of unifying understanding and generation. A collection of related resources is available at https://github.com/EmmaSRH/ARVFM.

OCMG-Net: Neural Oriented Normal Refinement for Unstructured Point Clouds

We present a robust refinement method for estimating oriented normals from unstructured point clouds. In contrast to previous approaches that either suffer from high computational complexity or fail to achieve desirable accuracy, our novel framework incorporates sign orientation and data augmentation in the feature space to refine the initial oriented normals, striking a balance between efficiency and accuracy. To address the issue of noise-caused direction inconsistency existing in previous approaches, we introduce a new metric called the Chamfer Normal Distance, which faithfully minimizes the estimation error by correcting the annotated normal with the closest point found on the potentially clean point cloud. This metric not only tackles the challenge but also aids in network training and significantly enhances network robustness against noise. Moreover, we propose an innovative dual-parallel architecture that integrates Multi-scale Local Feature Aggregation and Hierarchical Geometric Information Fusion, which enables the network to capture intricate geometric details more effectively and notably reduces ambiguity in scale selection. Extensive experiments demonstrate the superiority and versatility of our method in both unoriented and oriented normal estimation tasks across synthetic and real-world datasets among indoor and outdoor scenarios. The code is available at https://github.com/YingruiWoo/OCMG-Net.git.

Force Sensing Guided Artery-Vein Segmentation via Sequential Ultrasound Images

Accurate identification of arteries and veins in ultrasound images is crucial for vascular examinations and interventions in robotics-assisted surgeries. However, current methods for ultrasound vessel segmentation face challenges in distinguishing between arteries and veins due to their morphological similarities. To address this challenge, this study introduces a novel force sensing guided segmentation approach to enhance artery-vein segmentation accuracy by leveraging their distinct deformability. Our proposed method utilizes force magnitude to identify key frames with the most significant vascular deformation in a sequence of ultrasound images. These key frames are then integrated with the current frame through attention mechanisms, with weights assigned in accordance with force magnitude. Our proposed force sensing guided framework can be seamlessly integrated into various segmentation networks and achieves significant performance improvements in multiple U-shaped networks such as U-Net, Swin-unet and Transunet. Furthermore, we contribute the first multimodal ultrasound artery-vein segmentation dataset, Mus-V, which encompasses both force and image data simultaneously. The dataset comprises 3114 ultrasound images of carotid and femoral vessels extracted from 105 videos, with corresponding force data recorded by the force sensor mounted on the US probe. Our code and dataset will be publicly available.

Correspondence-Free Non-Rigid Point Set Registration Using Unsupervised Clustering Analysis

This paper presents a novel non-rigid point set registration method that is inspired by unsupervised clustering analysis. Unlike previous approaches that treat the source and target point sets as separate entities, we develop a holistic framework where they are formulated as clustering centroids and clustering members, separately. We then adopt Tikhonov regularization with an $\ell_1$-induced Laplacian kernel instead of the commonly used Gaussian kernel to ensure smooth and more robust displacement fields. Our formulation delivers closed-form solutions, theoretical guarantees, independence from dimensions, and the ability to handle large deformations. Subsequently, we introduce a clustering-improved Nystr\"om method to effectively reduce the computational complexity and storage of the Gram matrix to linear, while providing a rigorous bound for the low-rank approximation. Our method achieves high accuracy results across various scenarios and surpasses competitors by a significant margin, particularly on shapes with substantial deformations. Additionally, we demonstrate the versatility of our method in challenging tasks such as shape transfer and medical registration.

E$^3$-Net: Efficient E-Equivariant Normal Estimation Network

Point cloud normal estimation is a fundamental task in 3D geometry processing. While recent learning-based methods achieve notable advancements in normal prediction, they often overlook the critical aspect of equivariance. This results in inefficient learning of symmetric patterns. To address this issue, we propose E3-Net to achieve equivariance for normal estimation. We introduce an efficient random frame method, which significantly reduces the training resources required for this task to just 1/8 of previous work and improves the accuracy. Further, we design a Gaussian-weighted loss function and a receptive-aware inference strategy that effectively utilizes the local properties of point clouds. Our method achieves superior results on both synthetic and real-world datasets, and outperforms current state-of-the-art techniques by a substantial margin. We improve RMSE by 4% on the PCPNet dataset, 2.67% on the SceneNN dataset, and 2.44% on the FamousShape dataset.

CMG-Net: Robust Normal Estimation for Point Clouds via Chamfer Normal Distance and Multi-scale Geometry

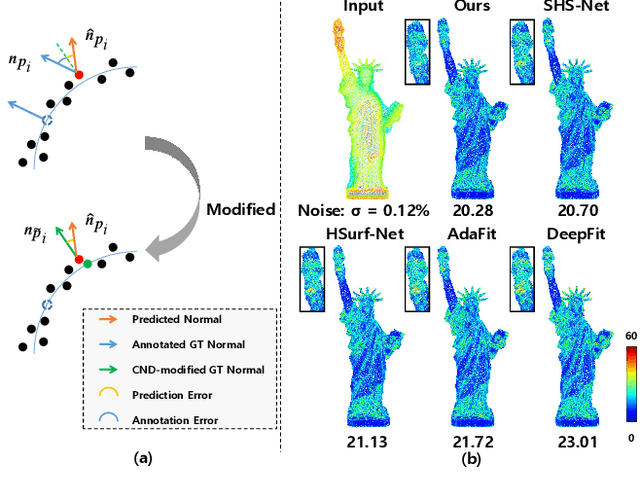
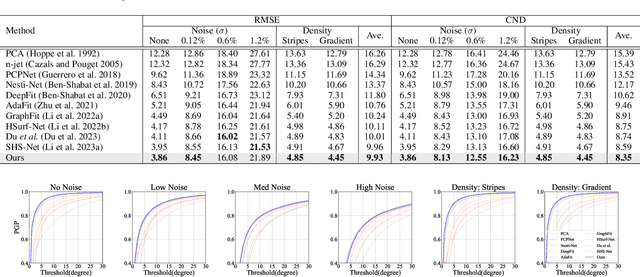
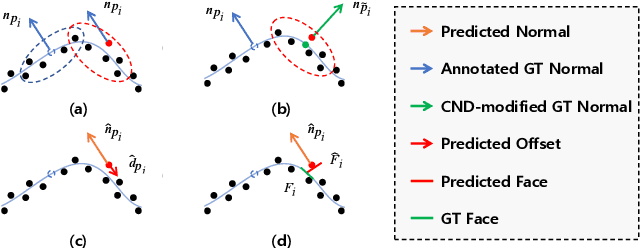
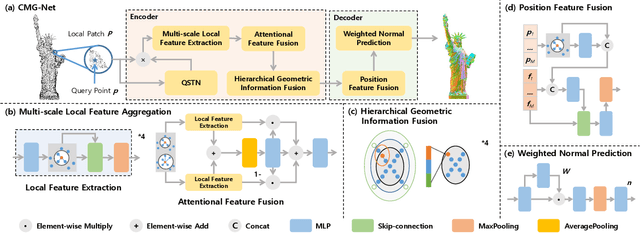
This work presents an accurate and robust method for estimating normals from point clouds. In contrast to predecessor approaches that minimize the deviations between the annotated and the predicted normals directly, leading to direction inconsistency, we first propose a new metric termed Chamfer Normal Distance to address this issue. This not only mitigates the challenge but also facilitates network training and substantially enhances the network robustness against noise. Subsequently, we devise an innovative architecture that encompasses Multi-scale Local Feature Aggregation and Hierarchical Geometric Information Fusion. This design empowers the network to capture intricate geometric details more effectively and alleviate the ambiguity in scale selection. Extensive experiments demonstrate that our method achieves the state-of-the-art performance on both synthetic and real-world datasets, particularly in scenarios contaminated by noise. Our implementation is available at https://github.com/YingruiWoo/CMG-Net_Pytorch.

Dimensionality Reduced Antenna Array for Beamforming/steering

Beamforming makes possible a focused communication method. It is extensively employed in many disciplines involving electromagnetic waves, including arrayed ultrasonic, optical, and high-speed wireless communication. Conventional beam steering often requires the addition of separate active amplitude phase control units after each radiating element. The high power consumption and complexity of large-scale phased arrays can be overcome by reducing the number of active controllers, pushing beamforming into satellite communications and deep space exploration. Here, we suggest a brand-new design for a phased array antenna with a dimension reduced cascaded angle offset (DRCAO-PAA). Furthermore, the suggested DRCAO-PAA was compressed by using the concept of singular value deposition. To pave the way for practical application the particle swarm optimization algorithm and deep neural network Transformer were adopted. Based on this theoretical framework, an experimental board was built to verify the theory. Finally, the 16/8/4 -array beam steering was demonstrated by using 4/3/2 active controllers, respectively.

GraphFit: Learning Multi-scale Graph-Convolutional Representation for Point Cloud Normal Estimation

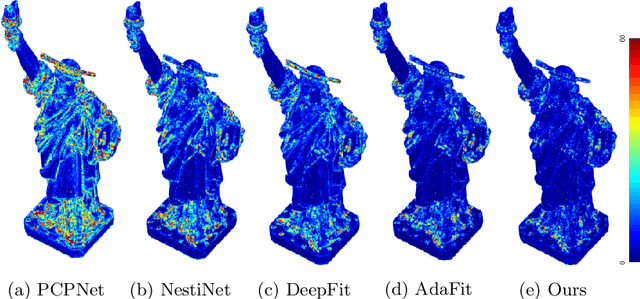
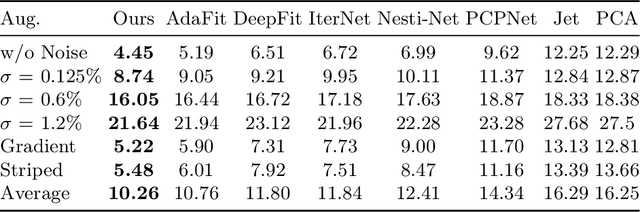
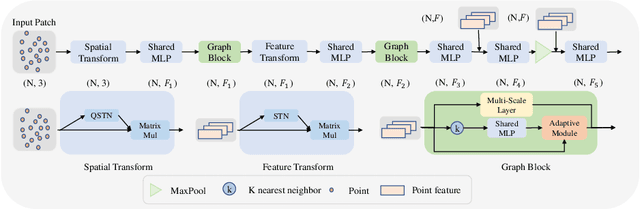
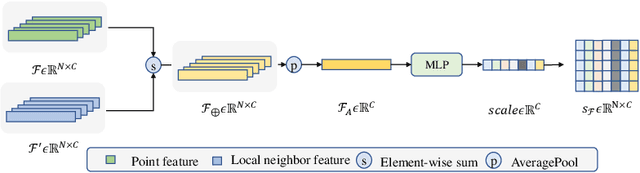
We propose a precise and efficient normal estimation method that can deal with noise and nonuniform density for unstructured 3D point clouds. Unlike existing approaches that directly take patches and ignore the local neighborhood relationships, which make them susceptible to challenging regions such as sharp edges, we propose to learn graph convolutional feature representation for normal estimation, which emphasizes more local neighborhood geometry and effectively encodes intrinsic relationships. Additionally, we design a novel adaptive module based on the attention mechanism to integrate point features with their neighboring features, hence further enhancing the robustness of the proposed normal estimator against point density variations. To make it more distinguishable, we introduce a multi-scale architecture in the graph block to learn richer geometric features. Our method outperforms competitors with the state-of-the-art accuracy on various benchmark datasets, and is quite robust against noise, outliers, as well as the density variations.

Robust Multi-view Registration of Point Sets with Laplacian Mixture Model

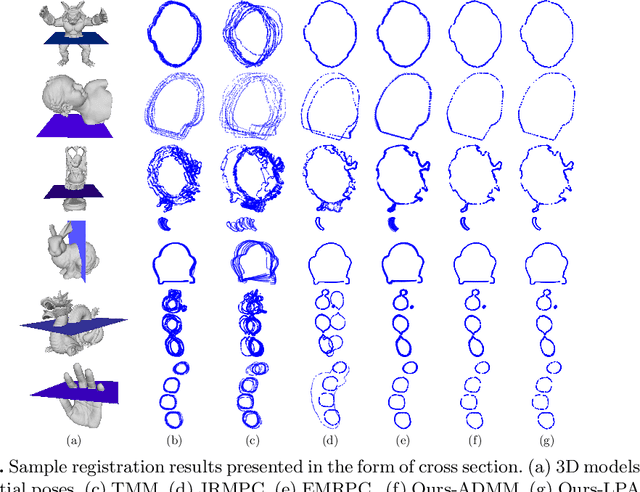
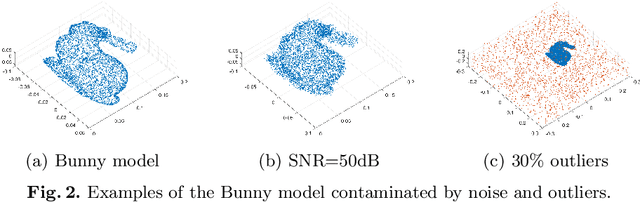
Point set registration is an essential step in many computer vision applications, such as 3D reconstruction and SLAM. Although there exist many registration algorithms for different purposes, however, this topic is still challenging due to the increasing complexity of various real-world scenarios, such as heavy noise and outlier contamination. In this paper, we propose a novel probabilistic generative method to simultaneously align multiple point sets based on the heavy-tailed Laplacian distribution. The proposed method assumes each data point is generated by a Laplacian Mixture Model (LMM), where its centers are determined by the corresponding points in other point sets. Different from the previous Gaussian Mixture Model (GMM) based method, which minimizes the quadratic distance between points and centers of Gaussian probability density, LMM minimizes the sparsity-induced L1 distance, thereby it is more robust against noise and outliers. We adopt Expectation-Maximization (EM) framework to solve LMM parameters and rigid transformations. We approximate the L1 optimization as a linear programming problem by exponential mapping in Lie algebra, which can be effectively solved through the interior point method. To improve efficiency, we also solve the L1 optimization by Alternating Direction Multiplier Method (ADMM). We demonstrate the advantages of our method by comparing it with representative state-of-the-art approaches on benchmark challenging data sets, in terms of robustness and accuracy.