Robust Multi-view Registration of Point Sets with Laplacian Mixture Model
Paper and Code
Oct 26, 2021
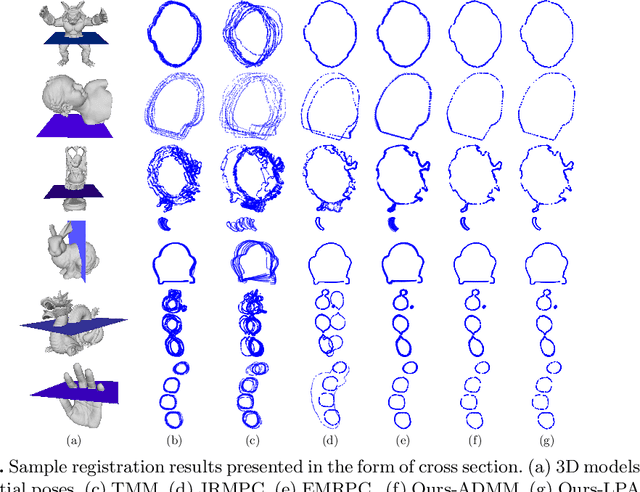

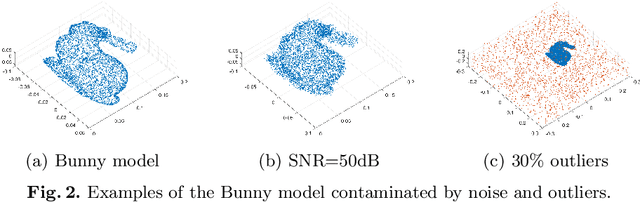
Point set registration is an essential step in many computer vision applications, such as 3D reconstruction and SLAM. Although there exist many registration algorithms for different purposes, however, this topic is still challenging due to the increasing complexity of various real-world scenarios, such as heavy noise and outlier contamination. In this paper, we propose a novel probabilistic generative method to simultaneously align multiple point sets based on the heavy-tailed Laplacian distribution. The proposed method assumes each data point is generated by a Laplacian Mixture Model (LMM), where its centers are determined by the corresponding points in other point sets. Different from the previous Gaussian Mixture Model (GMM) based method, which minimizes the quadratic distance between points and centers of Gaussian probability density, LMM minimizes the sparsity-induced L1 distance, thereby it is more robust against noise and outliers. We adopt Expectation-Maximization (EM) framework to solve LMM parameters and rigid transformations. We approximate the L1 optimization as a linear programming problem by exponential mapping in Lie algebra, which can be effectively solved through the interior point method. To improve efficiency, we also solve the L1 optimization by Alternating Direction Multiplier Method (ADMM). We demonstrate the advantages of our method by comparing it with representative state-of-the-art approaches on benchmark challenging data sets, in terms of robustness and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge