Evaluate Geometry of Radiance Field with Low-frequency Color Prior

Radiance field is an effective representation of 3D scenes, which has been widely adopted in novel-view synthesis and 3D reconstruction. It is still an open and challenging problem to evaluate the geometry, i.e., the density field, as the ground-truth is almost impossible to be obtained. One alternative indirect solution is to transform the density field into a point-cloud and compute its Chamfer Distance with the scanned ground-truth. However, many widely-used datasets have no point-cloud ground-truth since the scanning process along with the equipment is expensive and complicated. To this end, we propose a novel metric, named Inverse Mean Residual Color (IMRC), which can evaluate the geometry only with the observation images. Our key insight is that the better the geometry is, the lower-frequency the computed color field is. From this insight, given reconstructed density field and the observation images, we design a closed-form method to approximate the color field with low-frequency spherical harmonics and compute the inverse mean residual color. Then the higher the IMRC, the better the geometry. Qualitative and quantitative experimental results verify the effectiveness of our proposed IMRC metric. We also benchmark several state-of-the-art methods using IMRC to promote future related research.

GraphFit: Learning Multi-scale Graph-Convolutional Representation for Point Cloud Normal Estimation

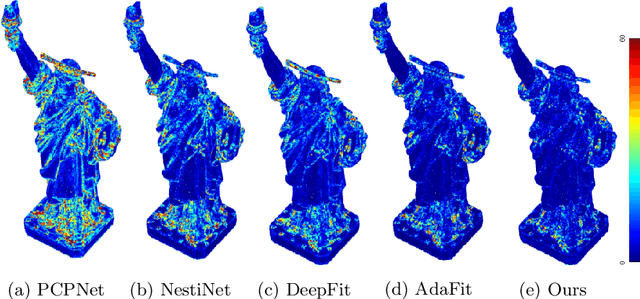
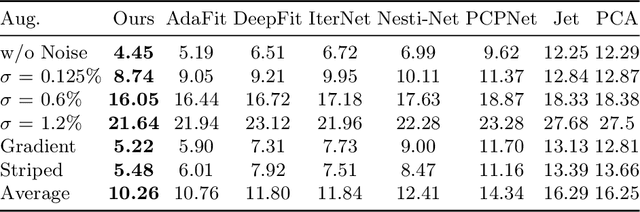
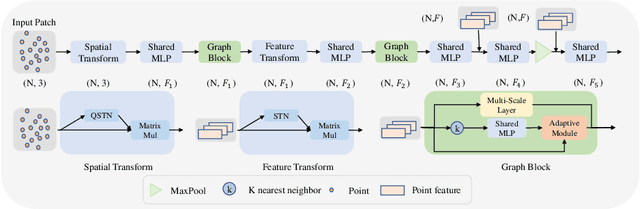
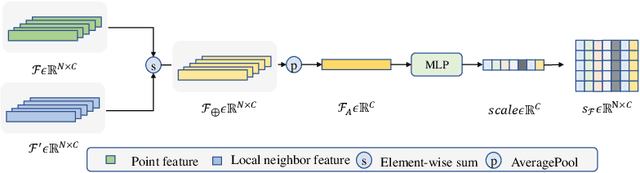
We propose a precise and efficient normal estimation method that can deal with noise and nonuniform density for unstructured 3D point clouds. Unlike existing approaches that directly take patches and ignore the local neighborhood relationships, which make them susceptible to challenging regions such as sharp edges, we propose to learn graph convolutional feature representation for normal estimation, which emphasizes more local neighborhood geometry and effectively encodes intrinsic relationships. Additionally, we design a novel adaptive module based on the attention mechanism to integrate point features with their neighboring features, hence further enhancing the robustness of the proposed normal estimator against point density variations. To make it more distinguishable, we introduce a multi-scale architecture in the graph block to learn richer geometric features. Our method outperforms competitors with the state-of-the-art accuracy on various benchmark datasets, and is quite robust against noise, outliers, as well as the density variations.