Yan Lok Ko
Minimax AUC Fairness: Efficient Algorithm with Provable Convergence
Aug 22, 2022
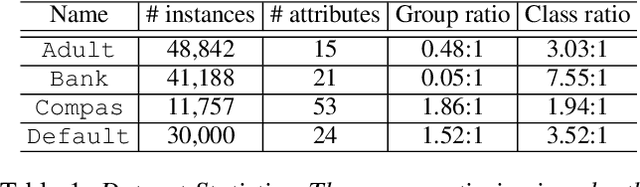


Abstract:The use of machine learning models in consequential decision making often exacerbates societal inequity, in particular yielding disparate impact on members of marginalized groups defined by race and gender. The area under the ROC curve (AUC) is widely used to evaluate the performance of a scoring function in machine learning, but is studied in algorithmic fairness less than other performance metrics. Due to the pairwise nature of the AUC, defining an AUC-based group fairness metric is pairwise-dependent and may involve both \emph{intra-group} and \emph{inter-group} AUCs. Importantly, considering only one category of AUCs is not sufficient to mitigate unfairness in AUC optimization. In this paper, we propose a minimax learning and bias mitigation framework that incorporates both intra-group and inter-group AUCs while maintaining utility. Based on this Rawlsian framework, we design an efficient stochastic optimization algorithm and prove its convergence to the minimum group-level AUC. We conduct numerical experiments on both synthetic and real-world datasets to validate the effectiveness of the minimax framework and the proposed optimization algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge