Fast Convergence of Softmax Policy Mirror Ascent

Natural policy gradient (NPG) is a common policy optimization algorithm and can be viewed as mirror ascent in the space of probabilities. Recently, Vaswani et al. [2021] introduced a policy gradient method that corresponds to mirror ascent in the dual space of logits. We refine this algorithm, removing its need for a normalization across actions and analyze the resulting method (referred to as SPMA). For tabular MDPs, we prove that SPMA with a constant step-size matches the linear convergence of NPG and achieves a faster convergence than constant step-size (accelerated) softmax policy gradient. To handle large state-action spaces, we extend SPMA to use a log-linear policy parameterization. Unlike that for NPG, generalizing SPMA to the linear function approximation (FA) setting does not require compatible function approximation. Unlike MDPO, a practical generalization of NPG, SPMA with linear FA only requires solving convex softmax classification problems. We prove that SPMA achieves linear convergence to the neighbourhood of the optimal value function. We extend SPMA to handle non-linear FA and evaluate its empirical performance on the MuJoCo and Atari benchmarks. Our results demonstrate that SPMA consistently achieves similar or better performance compared to MDPO, PPO and TRPO.

Noise-adaptive (Accelerated) Stochastic Heavy-Ball Momentum

We analyze the convergence of stochastic heavy ball (SHB) momentum in the smooth, strongly-convex setting. Kidambi et al. (2018) show that SHB (with small mini-batches) cannot attain an accelerated rate of convergence even for quadratics, and conjecture that the practical gain of SHB is a by-product of mini-batching. We substantiate this claim by showing that SHB can obtain an accelerated rate when the mini-batch size is larger than some threshold. In particular, for strongly-convex quadratics with condition number $\kappa$, we prove that SHB with the standard step-size and momentum parameters results in an $O\left(\exp(-\frac{T}{\sqrt{\kappa}}) + \sigma \right)$ convergence rate, where $T$ is the number of iterations and $\sigma^2$ is the variance in the stochastic gradients. To ensure convergence to the minimizer, we propose a multi-stage approach that results in a noise-adaptive $O\left(\exp\left(-\frac{T}{\sqrt{\kappa}} \right) + \frac{\sigma}{T}\right)$ rate. For general strongly-convex functions, we use the averaging interpretation of SHB along with exponential step-sizes to prove an $O\left(\exp\left(-\frac{T}{\kappa} \right) + \frac{\sigma^2}{T} \right)$ convergence to the minimizer in a noise-adaptive manner. Finally, we empirically demonstrate the effectiveness of the proposed algorithms.

Fast Online Node Labeling for Very Large Graphs

This paper studies the online node classification problem under a transductive learning setting. Current methods either invert a graph kernel matrix with $\mathcal{O}(n^3)$ runtime and $\mathcal{O}(n^2)$ space complexity or sample a large volume of random spanning trees, thus are difficult to scale to large graphs. In this work, we propose an improvement based on the \textit{online relaxation} technique introduced by a series of works (Rakhlin et al.,2012; Rakhlin and Sridharan, 2015; 2017). We first prove an effective regret $\mathcal{O}(\sqrt{n^{1+\gamma}})$ when suitable parameterized graph kernels are chosen, then propose an approximate algorithm FastONL enjoying $\mathcal{O}(k\sqrt{n^{1+\gamma}})$ regret based on this relaxation. The key of FastONL is a \textit{generalized local push} method that effectively approximates inverse matrix columns and applies to a series of popular kernels. Furthermore, the per-prediction cost is $\mathcal{O}(\text{vol}({\mathcal{S}})\log 1/\epsilon)$ locally dependent on the graph with linear memory cost. Experiments show that our scalable method enjoys a better tradeoff between local and global consistency.

Decision-Aware Actor-Critic with Function Approximation and Theoretical Guarantees

Actor-critic (AC) methods are widely used in reinforcement learning (RL) and benefit from the flexibility of using any policy gradient method as the actor and value-based method as the critic. The critic is usually trained by minimizing the TD error, an objective that is potentially decorrelated with the true goal of achieving a high reward with the actor. We address this mismatch by designing a joint objective for training the actor and critic in a decision-aware fashion. We use the proposed objective to design a generic, AC algorithm that can easily handle any function approximation. We explicitly characterize the conditions under which the resulting algorithm guarantees monotonic policy improvement, regardless of the choice of the policy and critic parameterization. Instantiating the generic algorithm results in an actor that involves maximizing a sequence of surrogate functions (similar to TRPO, PPO) and a critic that involves minimizing a closely connected objective. Using simple bandit examples, we provably establish the benefit of the proposed critic objective over the standard squared error. Finally, we empirically demonstrate the benefit of our decision-aware actor-critic framework on simple RL problems.

Target-based Surrogates for Stochastic Optimization

We consider minimizing functions for which it is expensive to compute the (possibly stochastic) gradient. Such functions are prevalent in reinforcement learning, imitation learning and adversarial training. Our target optimization framework uses the (expensive) gradient computation to construct surrogate functions in a target space (e.g. the logits output by a linear model for classification) that can be minimized efficiently. This allows for multiple parameter updates to the model, amortizing the cost of gradient computation. In the full-batch setting, we prove that our surrogate is a global upper-bound on the loss, and can be (locally) minimized using a black-box optimization algorithm. We prove that the resulting majorization-minimization algorithm ensures convergence to a stationary point of the loss. Next, we instantiate our framework in the stochastic setting and propose the $SSO$ algorithm, which can be viewed as projected stochastic gradient descent in the target space. This connection enables us to prove theoretical guarantees for $SSO$ when minimizing convex functions. Our framework allows the use of standard stochastic optimization algorithms to construct surrogates which can be minimized by any deterministic optimization method. To evaluate our framework, we consider a suite of supervised learning and imitation learning problems. Our experiments indicate the benefits of target optimization and the effectiveness of $SSO$.

Towards Painless Policy Optimization for Constrained MDPs

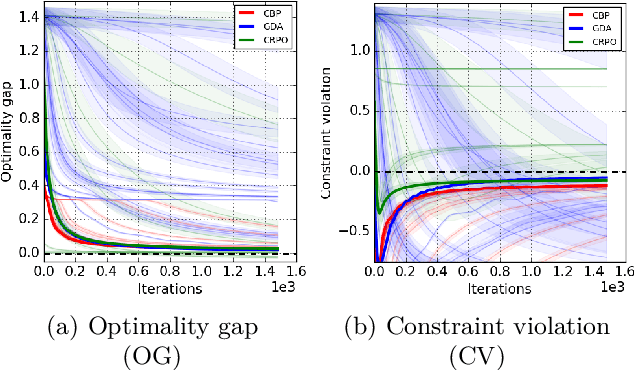
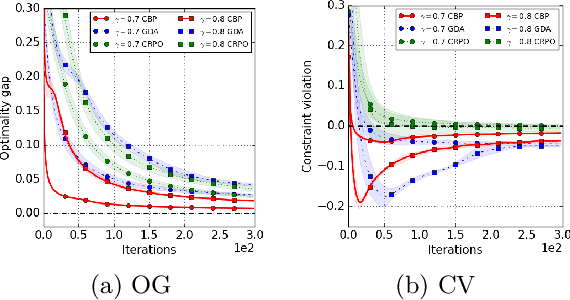
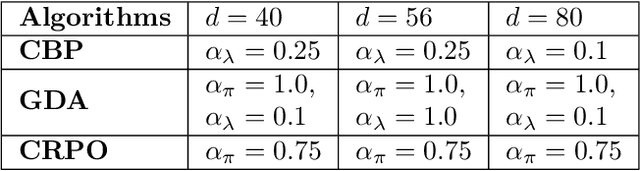
We study policy optimization in an infinite horizon, $\gamma$-discounted constrained Markov decision process (CMDP). Our objective is to return a policy that achieves large expected reward with a small constraint violation. We consider the online setting with linear function approximation and assume global access to the corresponding features. We propose a generic primal-dual framework that allows us to bound the reward sub-optimality and constraint violation for arbitrary algorithms in terms of their primal and dual regret on online linear optimization problems. We instantiate this framework to use coin-betting algorithms and propose the Coin Betting Politex (CBP) algorithm. Assuming that the action-value functions are $\varepsilon_b$-close to the span of the $d$-dimensional state-action features and no sampling errors, we prove that $T$ iterations of CBP result in an $O\left(\frac{1}{(1 - \gamma)^3 \sqrt{T}} + \frac{\varepsilon_b\sqrt{d}}{(1 - \gamma)^2} \right)$ reward sub-optimality and an $O\left(\frac{1}{(1 - \gamma)^2 \sqrt{T}} + \frac{\varepsilon_b \sqrt{d}}{1 - \gamma} \right)$ constraint violation. Importantly, unlike gradient descent-ascent and other recent methods, CBP does not require extensive hyperparameter tuning. Via experiments on synthetic and Cartpole environments, we demonstrate the effectiveness and robustness of CBP.

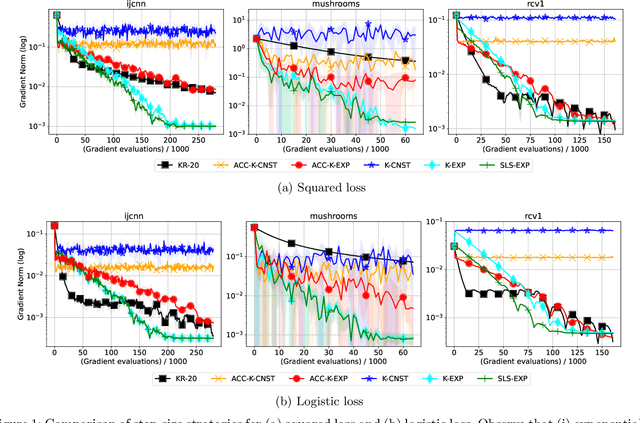
Towards Noise-adaptive, Problem-adaptive Stochastic Gradient Descent

We design step-size schemes that make stochastic gradient descent (SGD) adaptive to (i) the noise $\sigma^2$ in the stochastic gradients and (ii) problem-dependent constants. When minimizing smooth, strongly-convex functions with condition number $\kappa$, we first prove that $T$ iterations of SGD with Nesterov acceleration and exponentially decreasing step-sizes can achieve a near-optimal $\tilde{O}(\exp(-T/\sqrt{\kappa}) + \sigma^2/T)$ convergence rate. Under a relaxed assumption on the noise, with the same step-size scheme and knowledge of the smoothness, we prove that SGD can achieve an $\tilde{O}(\exp(-T/\kappa) + \sigma^2/T)$ rate. In order to be adaptive to the smoothness, we use a stochastic line-search (SLS) and show (via upper and lower-bounds) that SGD converges at the desired rate, but only to a neighbourhood of the solution. Next, we use SGD with an offline estimate of the smoothness and prove convergence to the minimizer. However, its convergence is slowed down proportional to the estimation error and we prove a lower-bound justifying this slowdown. Compared to other step-size schemes, we empirically demonstrate the effectiveness of exponential step-sizes coupled with a novel variant of SLS.

SVRG Meets AdaGrad: Painless Variance Reduction

Variance reduction (VR) methods for finite-sum minimization typically require the knowledge of problem-dependent constants that are often unknown and difficult to estimate. To address this, we use ideas from adaptive gradient methods to propose AdaSVRG, which is a fully adaptive variant of SVRG, a common VR method. AdaSVRG uses AdaGrad in the inner loop of SVRG, making it robust to the choice of step-size, and allowing it to adaptively determine the length of each inner-loop. When minimizing a sum of $n$ smooth convex functions, we prove that AdaSVRG requires $O(n + 1/\epsilon)$ gradient evaluations to achieve an $\epsilon$-suboptimality, matching the typical rate, but without needing to know problem-dependent constants. However, VR methods including AdaSVRG are slower than SGD when used with over-parameterized models capable of interpolating the training data. Hence, we also propose a hybrid algorithm that can adaptively switch from AdaGrad to AdaSVRG, achieving the best of both stochastic gradient and VR methods, but without needing to tune their step-sizes. Via experiments on synthetic and standard real-world datasets, we validate the robustness and effectiveness of AdaSVRG, demonstrating its superior performance over other "tune-free" VR methods.

Geometry-Aware Universal Mirror-Prox

Mirror-prox (MP) is a well-known algorithm to solve variational inequality (VI) problems. VI with a monotone operator covers a large group of settings such as convex minimization, min-max or saddle point problems. To get a convergent algorithm, the step-size of the classic MP algorithm relies heavily on the problem dependent knowledge of the operator such as its smoothness parameter which is hard to estimate. Recently, a universal variant of MP for smooth/bounded operators has been introduced that depends only on the norm of updates in MP. In this work, we relax the dependence to evaluating the norm of updates to Bregman divergence between updates. This relaxation allows us to extends the analysis of universal MP to the settings where the operator is not smooth or bounded. Furthermore, we analyse the VI problem with a stochastic monotone operator in different settings and obtain an optimal rate up to a logarithmic factor.

To Each Optimizer a Norm, To Each Norm its Generalization

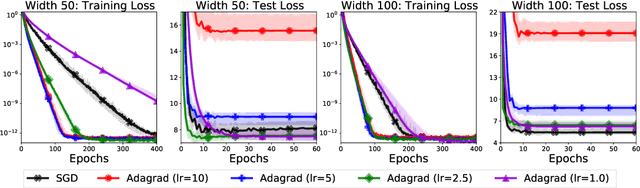
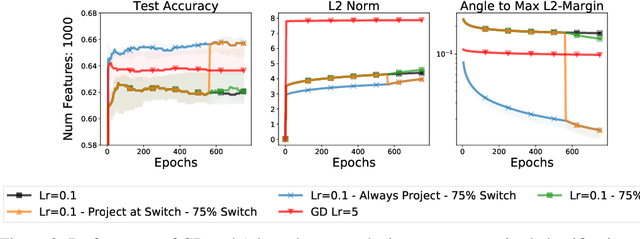
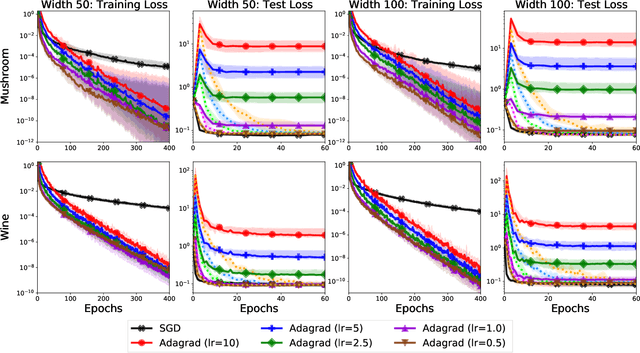
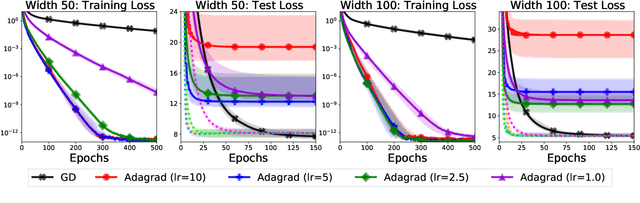
We study the implicit regularization of optimization methods for linear models interpolating the training data in the under-parametrized and over-parametrized regimes. Since it is difficult to determine whether an optimizer converges to solutions that minimize a known norm, we flip the problem and investigate what is the corresponding norm minimized by an interpolating solution. Using this reasoning, we prove that for over-parameterized linear regression, projections onto linear spans can be used to move between different interpolating solutions. For under-parameterized linear classification, we prove that for any linear classifier separating the data, there exists a family of quadratic norms ||.||_P such that the classifier's direction is the same as that of the maximum P-margin solution. For linear classification, we argue that analyzing convergence to the standard maximum l2-margin is arbitrary and show that minimizing the norm induced by the data results in better generalization. Furthermore, for over-parameterized linear classification, projections onto the data-span enable us to use techniques from the under-parameterized setting. On the empirical side, we propose techniques to bias optimizers towards better generalizing solutions, improving their test performance. We validate our theoretical results via synthetic experiments, and use the neural tangent kernel to handle non-linear models.