Fast Stochastic Composite Minimization and an Accelerated Frank-Wolfe Algorithm under Parallelization

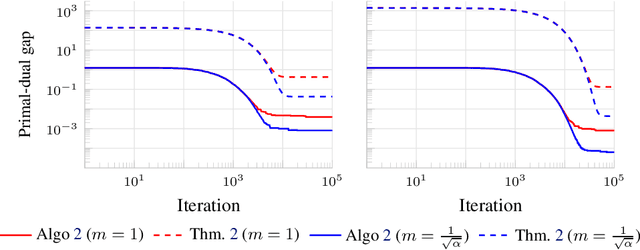
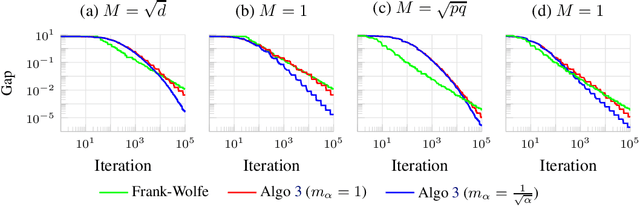
We consider the problem of minimizing the sum of two convex functions. One of those functions has Lipschitz-continuous gradients, and can be accessed via stochastic oracles, whereas the other is "simple". We provide a Bregman-type algorithm with accelerated convergence in function values to a ball containing the minimum. The radius of this ball depends on problem-dependent constants, including the variance of the stochastic oracle. We further show that this algorithmic setup naturally leads to a variant of Frank-Wolfe achieving acceleration under parallelization. More precisely, when minimizing a smooth convex function on a bounded domain, we show that one can achieve an $\epsilon$ primal-dual gap (in expectation) in $\tilde{O}(1/ \sqrt{\epsilon})$ iterations, by only accessing gradients of the original function and a linear maximization oracle with $O(1/\sqrt{\epsilon})$ computing units in parallel. We illustrate this fast convergence on synthetic numerical experiments.

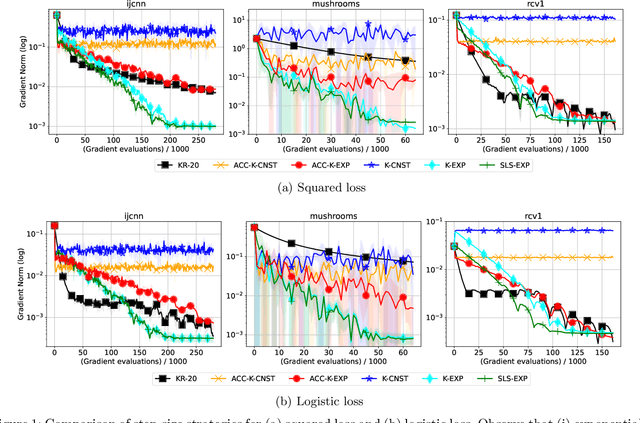
Towards Noise-adaptive, Problem-adaptive Stochastic Gradient Descent

We design step-size schemes that make stochastic gradient descent (SGD) adaptive to (i) the noise $\sigma^2$ in the stochastic gradients and (ii) problem-dependent constants. When minimizing smooth, strongly-convex functions with condition number $\kappa$, we first prove that $T$ iterations of SGD with Nesterov acceleration and exponentially decreasing step-sizes can achieve a near-optimal $\tilde{O}(\exp(-T/\sqrt{\kappa}) + \sigma^2/T)$ convergence rate. Under a relaxed assumption on the noise, with the same step-size scheme and knowledge of the smoothness, we prove that SGD can achieve an $\tilde{O}(\exp(-T/\kappa) + \sigma^2/T)$ rate. In order to be adaptive to the smoothness, we use a stochastic line-search (SLS) and show (via upper and lower-bounds) that SGD converges at the desired rate, but only to a neighbourhood of the solution. Next, we use SGD with an offline estimate of the smoothness and prove convergence to the minimizer. However, its convergence is slowed down proportional to the estimation error and we prove a lower-bound justifying this slowdown. Compared to other step-size schemes, we empirically demonstrate the effectiveness of exponential step-sizes coupled with a novel variant of SLS.

SVRG Meets AdaGrad: Painless Variance Reduction

Variance reduction (VR) methods for finite-sum minimization typically require the knowledge of problem-dependent constants that are often unknown and difficult to estimate. To address this, we use ideas from adaptive gradient methods to propose AdaSVRG, which is a fully adaptive variant of SVRG, a common VR method. AdaSVRG uses AdaGrad in the inner loop of SVRG, making it robust to the choice of step-size, and allowing it to adaptively determine the length of each inner-loop. When minimizing a sum of $n$ smooth convex functions, we prove that AdaSVRG requires $O(n + 1/\epsilon)$ gradient evaluations to achieve an $\epsilon$-suboptimality, matching the typical rate, but without needing to know problem-dependent constants. However, VR methods including AdaSVRG are slower than SGD when used with over-parameterized models capable of interpolating the training data. Hence, we also propose a hybrid algorithm that can adaptively switch from AdaGrad to AdaSVRG, achieving the best of both stochastic gradient and VR methods, but without needing to tune their step-sizes. Via experiments on synthetic and standard real-world datasets, we validate the robustness and effectiveness of AdaSVRG, demonstrating its superior performance over other "tune-free" VR methods.