Fast Stochastic Composite Minimization and an Accelerated Frank-Wolfe Algorithm under Parallelization
Paper and Code
May 25, 2022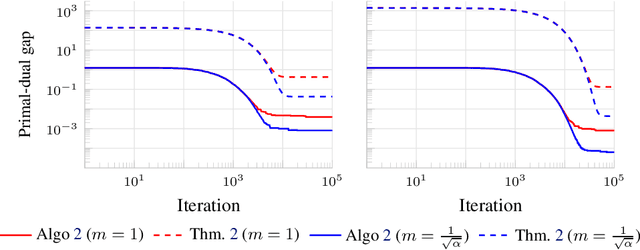
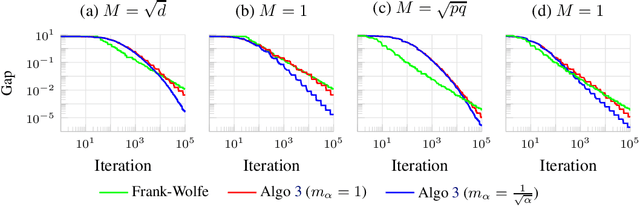
We consider the problem of minimizing the sum of two convex functions. One of those functions has Lipschitz-continuous gradients, and can be accessed via stochastic oracles, whereas the other is "simple". We provide a Bregman-type algorithm with accelerated convergence in function values to a ball containing the minimum. The radius of this ball depends on problem-dependent constants, including the variance of the stochastic oracle. We further show that this algorithmic setup naturally leads to a variant of Frank-Wolfe achieving acceleration under parallelization. More precisely, when minimizing a smooth convex function on a bounded domain, we show that one can achieve an $\epsilon$ primal-dual gap (in expectation) in $\tilde{O}(1/ \sqrt{\epsilon})$ iterations, by only accessing gradients of the original function and a linear maximization oracle with $O(1/\sqrt{\epsilon})$ computing units in parallel. We illustrate this fast convergence on synthetic numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge