Fast Stochastic Composite Minimization and an Accelerated Frank-Wolfe Algorithm under Parallelization

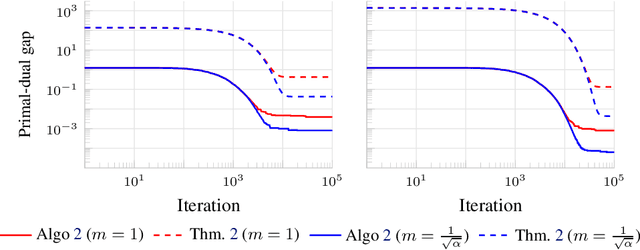
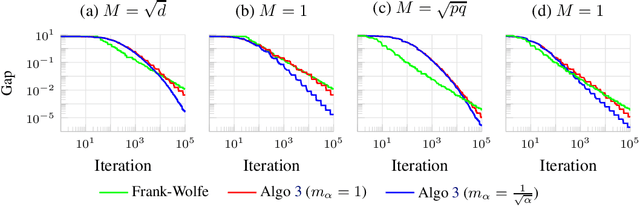
We consider the problem of minimizing the sum of two convex functions. One of those functions has Lipschitz-continuous gradients, and can be accessed via stochastic oracles, whereas the other is "simple". We provide a Bregman-type algorithm with accelerated convergence in function values to a ball containing the minimum. The radius of this ball depends on problem-dependent constants, including the variance of the stochastic oracle. We further show that this algorithmic setup naturally leads to a variant of Frank-Wolfe achieving acceleration under parallelization. More precisely, when minimizing a smooth convex function on a bounded domain, we show that one can achieve an $\epsilon$ primal-dual gap (in expectation) in $\tilde{O}(1/ \sqrt{\epsilon})$ iterations, by only accessing gradients of the original function and a linear maximization oracle with $O(1/\sqrt{\epsilon})$ computing units in parallel. We illustrate this fast convergence on synthetic numerical experiments.

PEPit: computer-assisted worst-case analyses of first-order optimization methods in Python

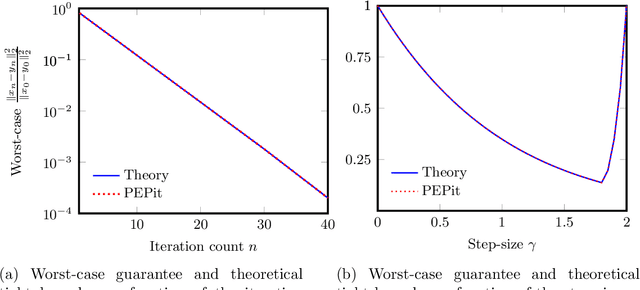
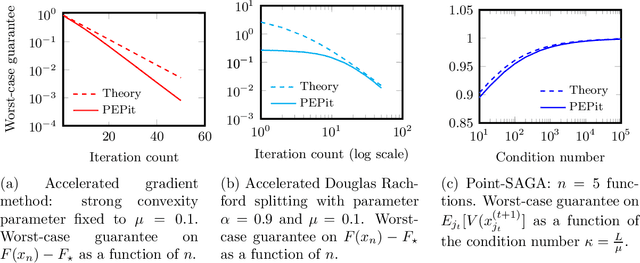
PEPit is a Python package aiming at simplifying the access to worst-case analyses of a large family of first-order optimization methods possibly involving gradient, projection, proximal, or linear optimization oracles, along with their approximate, or Bregman variants. In short, PEPit is a package enabling computer-assisted worst-case analyses of first-order optimization methods. The key underlying idea is to cast the problem of performing a worst-case analysis, often referred to as a performance estimation problem (PEP), as a semidefinite program (SDP) which can be solved numerically. For doing that, the package users are only required to write first-order methods nearly as they would have implemented them. The package then takes care of the SDP modelling parts, and the worst-case analysis is performed numerically via a standard solver.

A Continuized View on Nesterov Acceleration for Stochastic Gradient Descent and Randomized Gossip

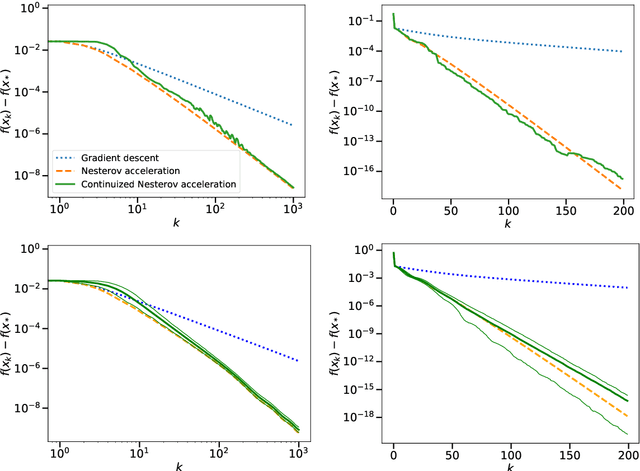
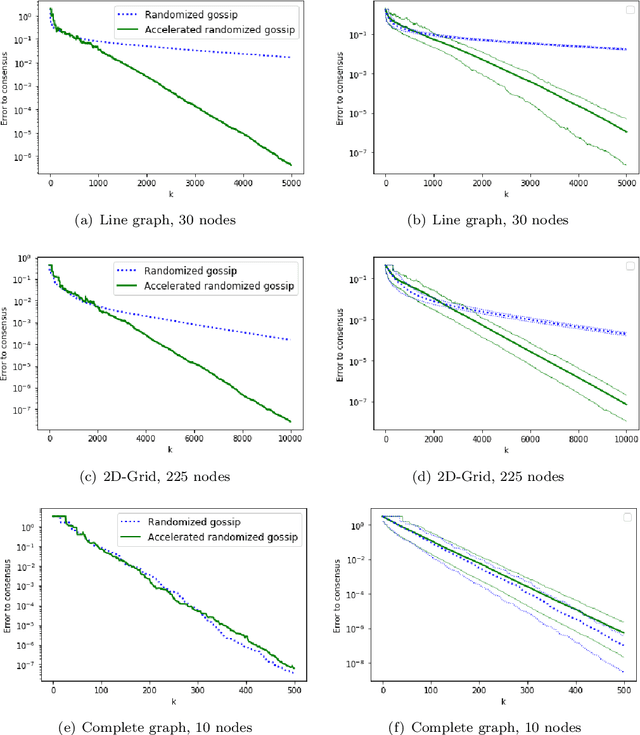
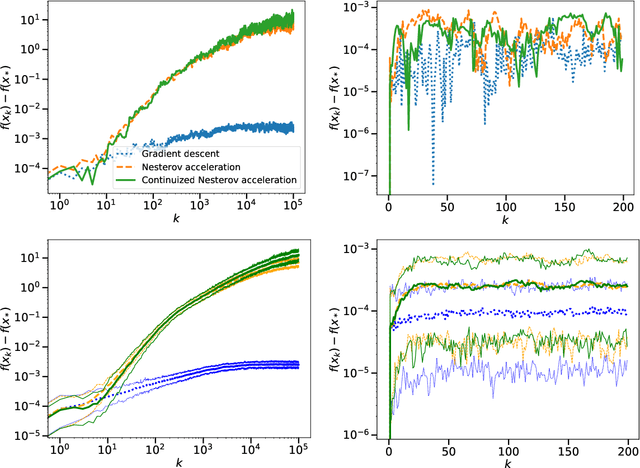
We introduce the continuized Nesterov acceleration, a close variant of Nesterov acceleration whose variables are indexed by a continuous time parameter. The two variables continuously mix following a linear ordinary differential equation and take gradient steps at random times. This continuized variant benefits from the best of the continuous and the discrete frameworks: as a continuous process, one can use differential calculus to analyze convergence and obtain analytical expressions for the parameters; and a discretization of the continuized process can be computed exactly with convergence rates similar to those of Nesterov original acceleration. We show that the discretization has the same structure as Nesterov acceleration, but with random parameters. We provide continuized Nesterov acceleration under deterministic as well as stochastic gradients, with either additive or multiplicative noise. Finally, using our continuized framework and expressing the gossip averaging problem as the stochastic minimization of a certain energy function, we provide the first rigorous acceleration of asynchronous gossip algorithms.

Acceleration Methods

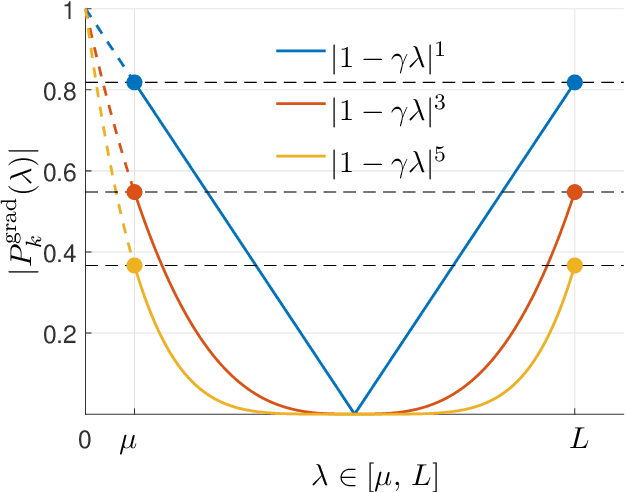
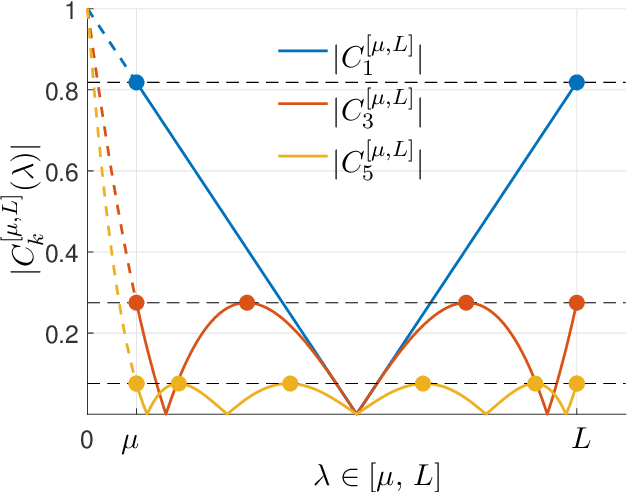
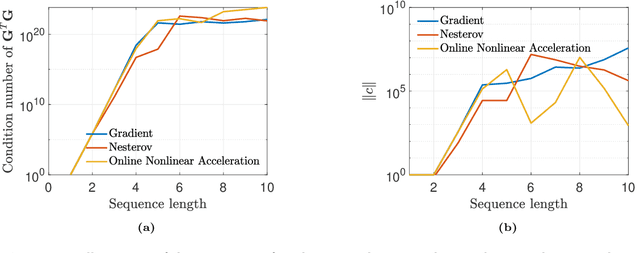
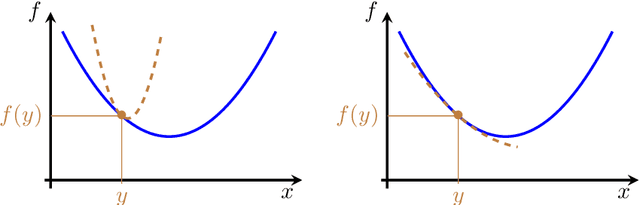
This monograph covers some recent advances on a range of acceleration techniques frequently used in convex optimization. We first use quadratic optimization problems to introduce two key families of methods, momentum and nested optimization schemes, which coincide in the quadratic case to form the Chebyshev method whose complexity is analyzed using Chebyshev polynomials. We discuss momentum methods in detail, starting with the seminal work of Nesterov (1983) and structure convergence proofs using a few master templates, such as that of \emph{optimized gradient methods} which have the key benefit of showing how momentum methods maximize convergence rates. We further cover proximal acceleration techniques, at the heart of the \emph{Catalyst} and \emph{Accelerated Hybrid Proximal Extragradient} frameworks, using similar algorithmic patterns. Common acceleration techniques directly rely on the knowledge of some regularity parameters of the problem at hand, and we conclude by discussing \emph{restart} schemes, a set of simple techniques to reach nearly optimal convergence rates while adapting to unobserved regularity parameters.

Complexity Guarantees for Polyak Steps with Momentum

In smooth strongly convex optimization, or in the presence of H\"olderian error bounds, knowledge of the curvature parameter is critical for obtaining simple methods with accelerated rates. In this work, we study a class of methods, based on Polyak steps, where this knowledge is substituted by that of the optimal value, $f_*$. We first show slightly improved convergence bounds than previously known for the classical case of simple gradient descent with Polyak steps, we then derive an accelerated gradient method with Polyak steps and momentum, along with convergence guarantees.

Stochastic first-order methods: non-asymptotic and computer-aided analyses via potential functions

We provide a novel computer-assisted technique for systematically analyzing first-order methods for optimization. In contrast with previous works, the approach is particularly suited for handling sublinear convergence rates and stochastic oracles. The technique relies on semidefinite programming and potential functions. It allows simultaneously obtaining worst-case guarantees on the behavior of those algorithms, and assisting in choosing appropriate parameters for tuning their worst-case performances. The technique also benefits from comfortable tightness guarantees, meaning that unsatisfactory results can be improved only by changing the setting. We use the approach for analyzing deterministic and stochastic first-order methods under different assumptions on the nature of the stochastic noise. Among others, we treat unstructured noise with bounded variance, different noise models arising in over-parametrized expectation minimization problems, and randomized block-coordinate descent schemes.