A discussion about violin reduction: geometric analysis of contour lines and channel of minima

Some early violins have been reduced during their history to fit imposed morphological standards, while more recent ones have been built directly to these standards. We can observe differences between reduced and unreduced instruments, particularly in their contour lines and channel of minima. In a recent preliminary work, we computed and highlighted those two features for two instruments using triangular 3D meshes acquired by photogrammetry, whose fidelity has been assessed and validated with sub-millimetre accuracy. We propose here an extension to a corpus of 38 violins, violas and cellos, and introduce improved procedures, leading to a stronger discussion of the geometric analysis. We first recall the material we are working with. We then discuss how to derive the best reference plane for the violin alignment, which is crucial for the computation of contour lines and channel of minima. Finally, we show how to compute efficiently both characteristics and we illustrate our results with a few examples.

Snacks: a fast large-scale kernel SVM solver

Kernel methods provide a powerful framework for non parametric learning. They are based on kernel functions and allow learning in a rich functional space while applying linear statistical learning tools, such as Ridge Regression or Support Vector Machines. However, standard kernel methods suffer from a quadratic time and memory complexity in the number of data points and thus have limited applications in large-scale learning. In this paper, we propose Snacks, a new large-scale solver for Kernel Support Vector Machines. Specifically, Snacks relies on a Nystr\"om approximation of the kernel matrix and an accelerated variant of the stochastic subgradient method. We demonstrate formally through a detailed empirical evaluation, that it competes with other SVM solvers on a variety of benchmark datasets.

Least-squares methods for nonnegative matrix factorization over rational functions

Nonnegative Matrix Factorization (NMF) models are widely used to recover linearly mixed nonnegative data. When the data is made of samplings of continuous signals, the factors in NMF can be constrained to be samples of nonnegative rational functions, which allow fairly general models; this is referred to as NMF using rational functions (R-NMF). We first show that, under mild assumptions, R-NMF has an essentially unique factorization unlike NMF, which is crucial in applications where ground-truth factors need to be recovered such as blind source separation problems. Then we present different approaches to solve R-NMF: the R-HANLS, R-ANLS and R-NLS methods. From our tests, no method significantly outperforms the others, and a trade-off should be done between time and accuracy. Indeed, R-HANLS is fast and accurate for large problems, while R-ANLS is more accurate, but also more resources demanding, both in time and memory. R-NLS is very accurate but only for small problems. Moreover, we show that R-NMF outperforms NMF in various tasks including the recovery of semi-synthetic continuous signals, and a classification problem of real hyperspectral signals.

Validation of a photogrammetric approach for the study of ancient bowed instruments

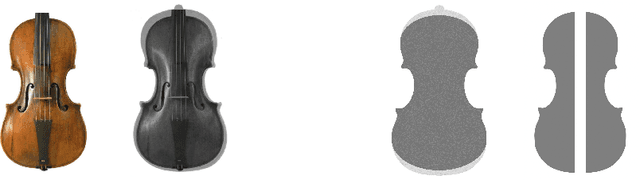
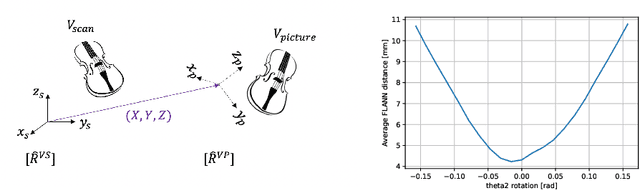
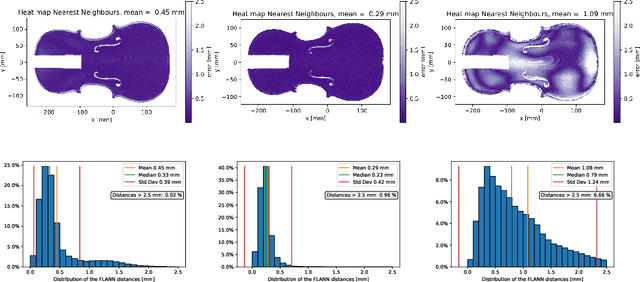
Some ancient violins have been reduced throughout their history. We propose an objective photogrammetric approach to differentiate between a reduced and an unreduced instrument, where a three-dimensional mesh is studied geometrically by examining 2D slices. First, we validate the accuracy of the photogrammetric mesh by the way of a comparison with reference images obtained with medical imaging. Then, we show how contour lines and channels of minima can be automatically extracted from the photogrammetric meshes, allowing to successfully highlight differences between instruments.

A two-level machine learning framework for predictive maintenance: comparison of learning formulations

Predicting incoming failures and scheduling maintenance based on sensors information in industrial machines is increasingly important to avoid downtime and machine failure. Different machine learning formulations can be used to solve the predictive maintenance problem. However, many of the approaches studied in the literature are not directly applicable to real-life scenarios. Indeed, many of those approaches usually either rely on labelled machine malfunctions in the case of classification and fault detection, or rely on finding a monotonic health indicator on which a prediction can be made in the case of regression and remaining useful life estimation, which is not always feasible. Moreover, the decision-making part of the problem is not always studied in conjunction with the prediction phase. This paper aims to design and compare different formulations for predictive maintenance in a two-level framework and design metrics that quantify both the failure detection performance as well as the timing of the maintenance decision. The first level is responsible for building a health indicator by aggregating features using a learning algorithm. The second level consists of a decision-making system that can trigger an alarm based on this health indicator. Three degrees of refinements are compared in the first level of the framework, from simple threshold-based univariate predictive technique to supervised learning methods based on the remaining time before failure. We choose to use the Support Vector Machine (SVM) and its variations as the common algorithm used in all the formulations. We apply and compare the different strategies on a real-world rotating machine case study and observe that while a simple model can already perform well, more sophisticated refinements enhance the predictions for well-chosen parameters.

PEPit: computer-assisted worst-case analyses of first-order optimization methods in Python

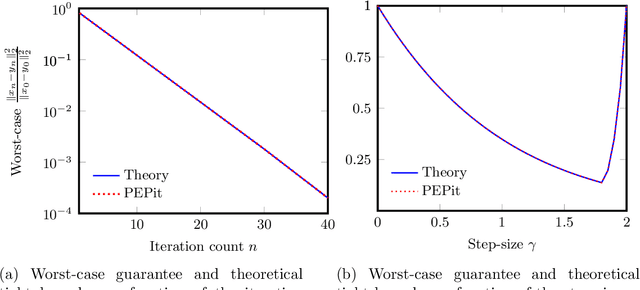
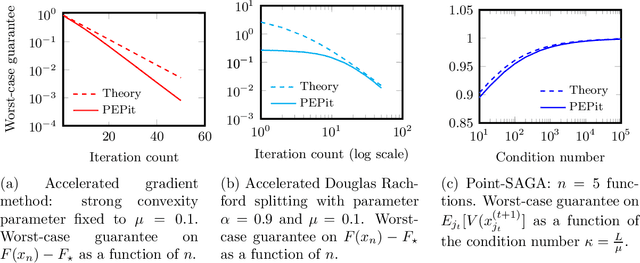
PEPit is a Python package aiming at simplifying the access to worst-case analyses of a large family of first-order optimization methods possibly involving gradient, projection, proximal, or linear optimization oracles, along with their approximate, or Bregman variants. In short, PEPit is a package enabling computer-assisted worst-case analyses of first-order optimization methods. The key underlying idea is to cast the problem of performing a worst-case analysis, often referred to as a performance estimation problem (PEP), as a semidefinite program (SDP) which can be solved numerically. For doing that, the package users are only required to write first-order methods nearly as they would have implemented them. The package then takes care of the SDP modelling parts, and the worst-case analysis is performed numerically via a standard solver.

New Riemannian preconditioned algorithms for tensor completion via polyadic decomposition

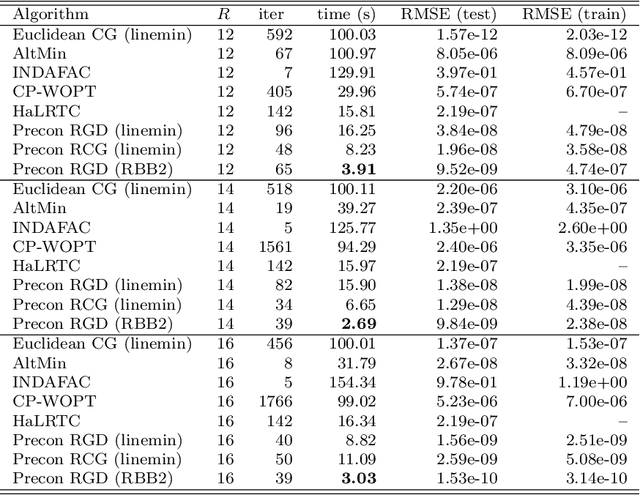
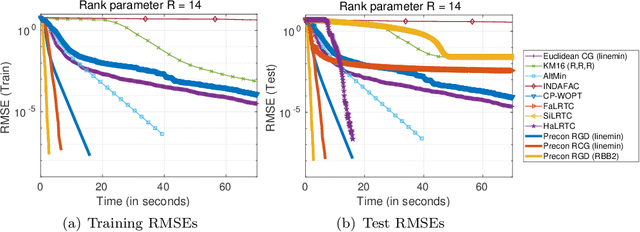
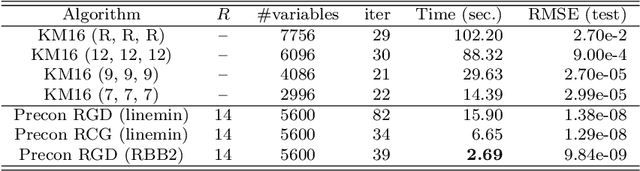
We propose new Riemannian preconditioned algorithms for low-rank tensor completion via the polyadic decomposition of a tensor. These algorithms exploit a non-Euclidean metric on the product space of the factor matrices of the low-rank tensor in the polyadic decomposition form. This new metric is designed using an approximation of the diagonal blocks of the Hessian of the tensor completion cost function, thus has a preconditioning effect on these algorithms. We prove that the proposed Riemannian gradient descent algorithm globally converges to a stationary point of the tensor completion problem, with convergence rate estimates using the $\L{}$ojasiewicz property. Numerical results on synthetic and real-world data suggest that the proposed algorithms are more efficient in memory and time compared to state-of-the-art algorithms. Moreover, the proposed algorithms display a greater tolerance for overestimated rank parameters in terms of the tensor recovery performance, thus enable a flexible choice of the rank parameter.

Alternating minimization algorithms for graph regularized tensor completion

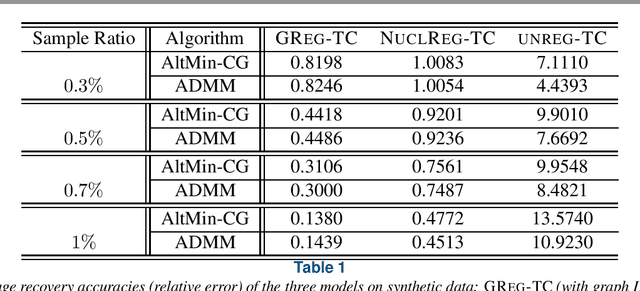
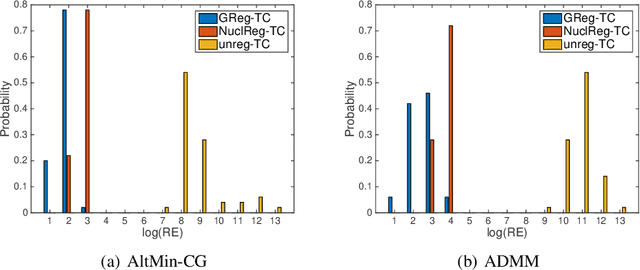
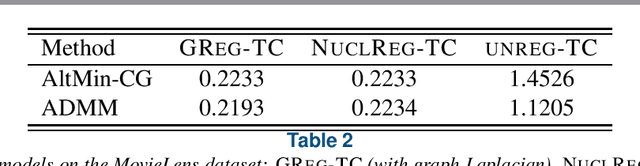
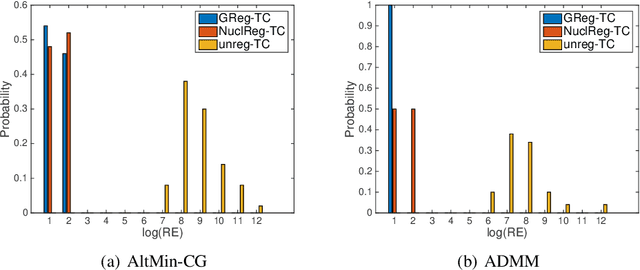
We consider a low-rank tensor completion (LRTC) problem which aims to recover a tensor from incomplete observations. LRTC plays an important role in many applications such as signal processing, computer vision, machine learning, and neuroscience. A widely used approach is to combine the tensor completion data fitting term with a regularizer based on a convex relaxation of the multilinear ranks of the tensor. For the data fitting function, we model the tensor variable by using the Canonical Polyadic (CP) decomposition and for the low-rank promoting regularization function, we consider a graph Laplacian-based function which exploits correlations between the rows of the matrix unfoldings. For solving our LRTC model, we propose an efficient alternating minimization algorithm. Furthermore, based on the Kurdyka-{\L}ojasiewicz property, we show that the sequence generated by the proposed algorithm globally converges to a critical point of the objective function. Besides, an alternating direction method of multipliers algorithm is also developed for the LRTC model. Extensive numerical experiments on synthetic and real data indicate that the proposed algorithms are effective and efficient.

Heuristics for Exact Nonnegative Matrix Factorization

The exact nonnegative matrix factorization (exact NMF) problem is the following: given an $m$-by-$n$ nonnegative matrix $X$ and a factorization rank $r$, find, if possible, an $m$-by-$r$ nonnegative matrix $W$ and an $r$-by-$n$ nonnegative matrix $H$ such that $X = WH$. In this paper, we propose two heuristics for exact NMF, one inspired from simulated annealing and the other from the greedy randomized adaptive search procedure. We show that these two heuristics are able to compute exact nonnegative factorizations for several classes of nonnegative matrices (namely, linear Euclidean distance matrices, slack matrices, unique-disjointness matrices, and randomly generated matrices) and as such demonstrate their superiority over standard multi-start strategies. We also consider a hybridization between these two heuristics that allows us to combine the advantages of both methods. Finally, we discuss the use of these heuristics to gain insight on the behavior of the nonnegative rank, i.e., the minimum factorization rank such that an exact NMF exists. In particular, we disprove a conjecture on the nonnegative rank of a Kronecker product, propose a new upper bound on the extension complexity of generic $n$-gons and conjecture the exact value of (i) the extension complexity of regular $n$-gons and (ii) the nonnegative rank of a submatrix of the slack matrix of the correlation polytope.