DCDILP: a distributed learning method for large-scale causal structure learning

This paper presents a novel approach to causal discovery through a divide-and-conquer framework. By decomposing the problem into smaller subproblems defined on Markov blankets, the proposed DCDILP method first explores in parallel the local causal graphs of these subproblems. However, this local discovery phase encounters systematic challenges due to the presence of hidden confounders (variables within each Markov blanket may be influenced by external variables). Moreover, aggregating these local causal graphs in a consistent global graph defines a large size combinatorial optimization problem. DCDILP addresses these challenges by: i) restricting the local subgraphs to causal links only related with the central variable of the Markov blanket; ii) formulating the reconciliation of local causal graphs as an integer linear programming method. The merits of the approach, in both terms of causal discovery accuracy and scalability in the size of the problem, are showcased by experiments and comparisons with the state of the art.

High-Dimensional Causal Discovery: Learning from Inverse Covariance via Independence-based Decomposition

Inferring causal relationships from observational data is a fundamental yet highly complex problem when the number of variables is large. Recent advances have made much progress in learning causal structure models (SEMs) but still face challenges in scalability. This paper aims to efficiently discover causal DAGs from high-dimensional data. We investigate a way of recovering causal DAGs from inverse covariance estimators of the observational data. The proposed algorithm, called ICID (inverse covariance estimation and {\it independence-based} decomposition), searches for a decomposition of the inverse covariance matrix that preserves its nonzero patterns. This algorithm benefits from properties of positive definite matrices supported on {\it chordal} graphs and the preservation of nonzero patterns in their Cholesky decomposition; we find exact mirroring between the support-preserving property and the independence-preserving property of our decomposition method, which explains its effectiveness in identifying causal structures from the data distribution. We show that the proposed algorithm recovers causal DAGs with a complexity of $O(d^2)$ in the context of sparse SEMs. The advantageously low complexity is reflected by good scalability of our algorithm in thorough experiments and comparisons with state-of-the-art algorithms.

From graphs to DAGs: a low-complexity model and a scalable algorithm

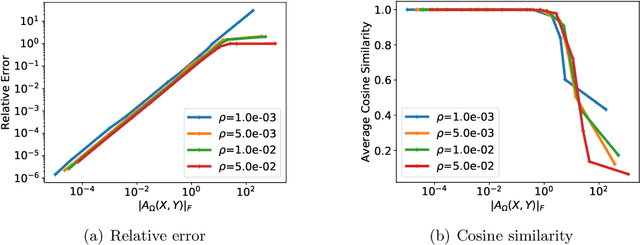
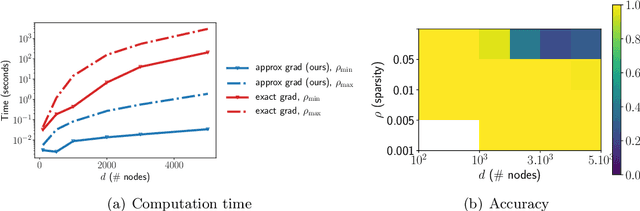
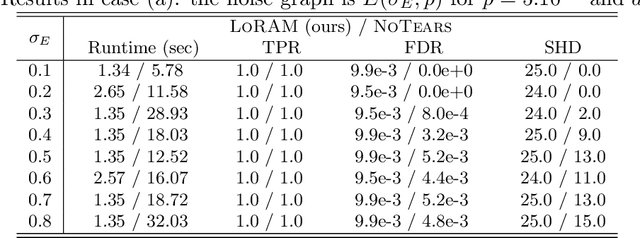
Learning directed acyclic graphs (DAGs) is long known a critical challenge at the core of probabilistic and causal modeling. The NoTears approach of (Zheng et al., 2018), through a differentiable function involving the matrix exponential trace $\mathrm{tr}(\exp(\cdot))$, opens up a way to learning DAGs via continuous optimization, though with a $O(d^3)$ complexity in the number $d$ of nodes. This paper presents a low-complexity model, called LoRAM for Low-Rank Additive Model, which combines low-rank matrix factorization with a sparsification mechanism for the continuous optimization of DAGs. The main contribution of the approach lies in an efficient gradient approximation method leveraging the low-rank property of the model, and its straightforward application to the computation of projections from graph matrices onto the DAG matrix space. The proposed method achieves a reduction from a cubic complexity to quadratic complexity while handling the same DAG characteristic function as NoTears, and scales easily up to thousands of nodes for the projection problem. The experiments show that the LoRAM achieves efficiency gains of orders of magnitude compared to the state-of-the-art at the expense of a very moderate accuracy loss in the considered range of sparse matrices, and with a low sensitivity to the rank choice of the model's low-rank component.

New Riemannian preconditioned algorithms for tensor completion via polyadic decomposition

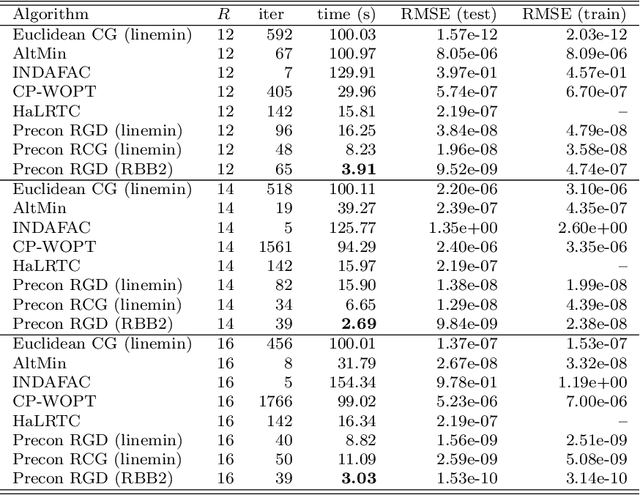
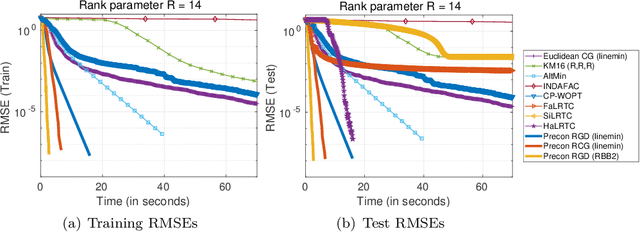
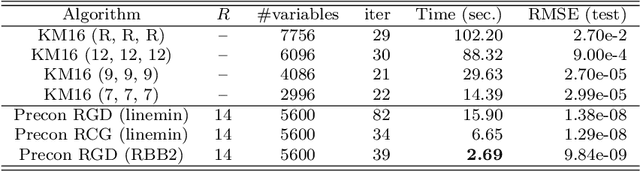
We propose new Riemannian preconditioned algorithms for low-rank tensor completion via the polyadic decomposition of a tensor. These algorithms exploit a non-Euclidean metric on the product space of the factor matrices of the low-rank tensor in the polyadic decomposition form. This new metric is designed using an approximation of the diagonal blocks of the Hessian of the tensor completion cost function, thus has a preconditioning effect on these algorithms. We prove that the proposed Riemannian gradient descent algorithm globally converges to a stationary point of the tensor completion problem, with convergence rate estimates using the $\L{}$ojasiewicz property. Numerical results on synthetic and real-world data suggest that the proposed algorithms are more efficient in memory and time compared to state-of-the-art algorithms. Moreover, the proposed algorithms display a greater tolerance for overestimated rank parameters in terms of the tensor recovery performance, thus enable a flexible choice of the rank parameter.

Alternating minimization algorithms for graph regularized tensor completion

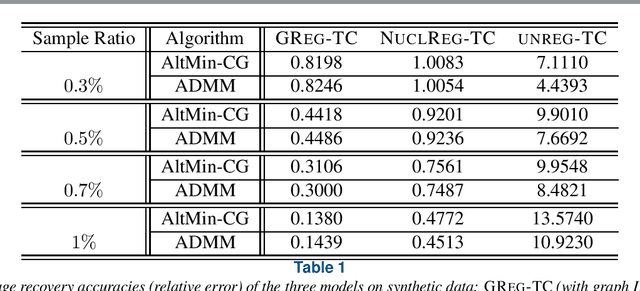
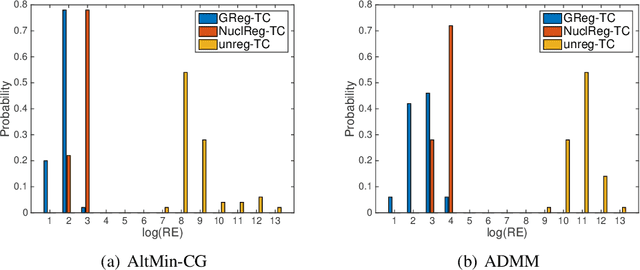
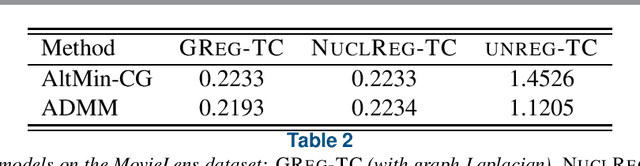
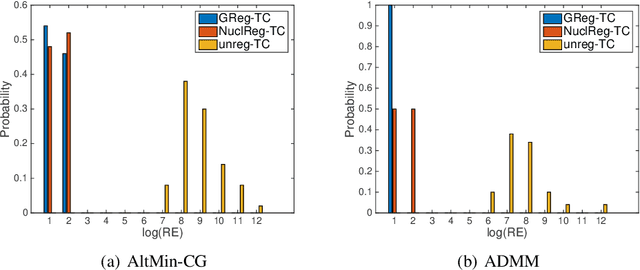
We consider a low-rank tensor completion (LRTC) problem which aims to recover a tensor from incomplete observations. LRTC plays an important role in many applications such as signal processing, computer vision, machine learning, and neuroscience. A widely used approach is to combine the tensor completion data fitting term with a regularizer based on a convex relaxation of the multilinear ranks of the tensor. For the data fitting function, we model the tensor variable by using the Canonical Polyadic (CP) decomposition and for the low-rank promoting regularization function, we consider a graph Laplacian-based function which exploits correlations between the rows of the matrix unfoldings. For solving our LRTC model, we propose an efficient alternating minimization algorithm. Furthermore, based on the Kurdyka-{\L}ojasiewicz property, we show that the sequence generated by the proposed algorithm globally converges to a critical point of the objective function. Besides, an alternating direction method of multipliers algorithm is also developed for the LRTC model. Extensive numerical experiments on synthetic and real data indicate that the proposed algorithms are effective and efficient.