Optimization without retraction on the random generalized Stiefel manifold

Optimization over the set of matrices that satisfy $X^\top B X = I_p$, referred to as the generalized Stiefel manifold, appears in many applications involving sampled covariance matrices such as canonical correlation analysis (CCA), independent component analysis (ICA), and the generalized eigenvalue problem (GEVP). Solving these problems is typically done by iterative methods, such as Riemannian approaches, which require a computationally expensive eigenvalue decomposition involving fully formed $B$. We propose a cheap stochastic iterative method that solves the optimization problem while having access only to a random estimate of the feasible set. Our method does not enforce the constraint in every iteration exactly, but instead it produces iterations that converge to a critical point on the generalized Stiefel manifold defined in expectation. The method has lower per-iteration cost, requires only matrix multiplications, and has the same convergence rates as its Riemannian counterparts involving the full matrix $B$. Experiments demonstrate its effectiveness in various machine learning applications involving generalized orthogonality constraints, including CCA, ICA, and GEVP.

Graph-Based Matrix Completion Applied to Weather Data

Low-rank matrix completion is the task of recovering unknown entries of a matrix by assuming that the true matrix admits a good low-rank approximation. Sometimes additional information about the variables is known, and incorporating this information into a matrix completion model can lead to a better completion quality. We consider the situation where information between the column/row entities of the matrix is available as a weighted graph. In this framework, we address the problem of completing missing entries in air temperature data recorded by weather stations. We construct test sets by holding back data at locations that mimic real-life gaps in weather data. On such test sets, we show that adequate spatial and temporal graphs can significantly improve the accuracy of the completion obtained by graph-regularized low-rank matrix completion methods.

Infeasible Deterministic, Stochastic, and Variance-Reduction Algorithms for Optimization under Orthogonality Constraints

Orthogonality constraints naturally appear in many machine learning problems, from Principal Components Analysis to robust neural network training. They are usually solved using Riemannian optimization algorithms, which minimize the objective function while enforcing the constraint. However, enforcing the orthogonality constraint can be the most time-consuming operation in such algorithms. Recently, Ablin & Peyr\'e (2022) proposed the Landing algorithm, a method with cheap iterations that does not enforce the orthogonality constraint but is attracted towards the manifold in a smooth manner. In this article, we provide new practical and theoretical developments for the landing algorithm. First, the method is extended to the Stiefel manifold, the set of rectangular orthogonal matrices. We also consider stochastic and variance reduction algorithms when the cost function is an average of many functions. We demonstrate that all these methods have the same rate of convergence as their Riemannian counterparts that exactly enforce the constraint. Finally, our experiments demonstrate the promise of our approach to an array of machine-learning problems that involve orthogonality constraints.

Alternating minimization algorithms for graph regularized tensor completion

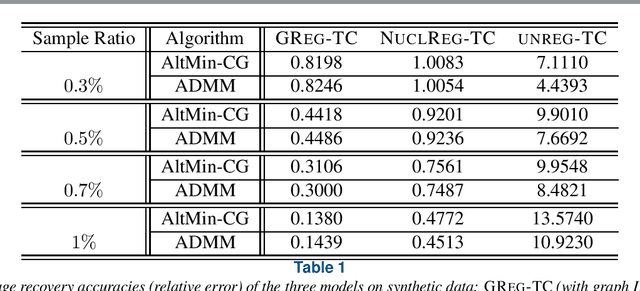
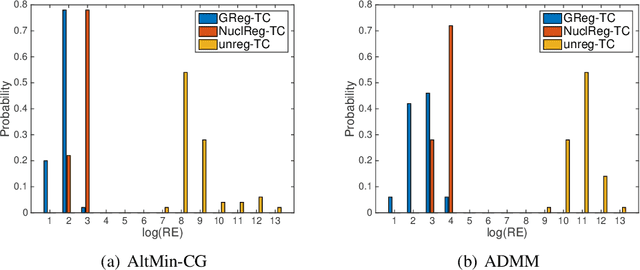
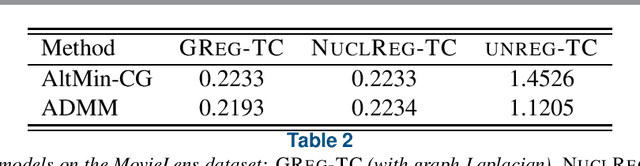
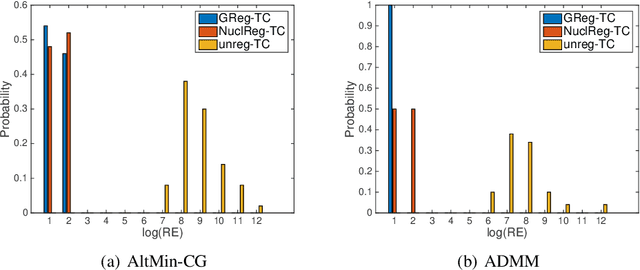
We consider a low-rank tensor completion (LRTC) problem which aims to recover a tensor from incomplete observations. LRTC plays an important role in many applications such as signal processing, computer vision, machine learning, and neuroscience. A widely used approach is to combine the tensor completion data fitting term with a regularizer based on a convex relaxation of the multilinear ranks of the tensor. For the data fitting function, we model the tensor variable by using the Canonical Polyadic (CP) decomposition and for the low-rank promoting regularization function, we consider a graph Laplacian-based function which exploits correlations between the rows of the matrix unfoldings. For solving our LRTC model, we propose an efficient alternating minimization algorithm. Furthermore, based on the Kurdyka-{\L}ojasiewicz property, we show that the sequence generated by the proposed algorithm globally converges to a critical point of the objective function. Besides, an alternating direction method of multipliers algorithm is also developed for the LRTC model. Extensive numerical experiments on synthetic and real data indicate that the proposed algorithms are effective and efficient.

Assessment of COVID-19 hospitalization forecasts from a simplified SIR model

We propose the SH model, a simplified version of the well-known SIR compartmental model of infectious diseases. With optimized parameters and initial conditions, this time-invariant two-parameter two-dimensional model is able to fit COVID-19 hospitalization data over several months with high accuracy (mean absolute percentage error below 15%). Moreover, we observed that, when the model is trained on a suitable two-week period around the hospitalization peak for Belgium, it forecasts the subsequent three-month decrease with mean absolute percentage error below 10%. However, when it is trained in the increase phase, it is less successful at forecasting the subsequent evolution.

On a minimum enclosing ball of a collection of linear subspaces

This paper concerns the minimax center of a collection of linear subspaces. When the subspaces are $k$-dimensional subspaces of $\mathbb{R}^n$, this can be cast as finding the center of a minimum enclosing ball on a Grassmann manifold, Gr$(k,n)$. For subspaces of different dimension, the setting becomes a disjoint union of Grassmannians rather than a single manifold, and the problem is no longer well-defined. However, natural geometric maps exist between these manifolds with a well-defined notion of distance for the images of the subspaces under the mappings. Solving the initial problem in this context leads to a candidate minimax center on each of the constituent manifolds, but does not inherently provide intuition about which candidate is the best representation of the data. Additionally, the solutions of different rank are generally not nested so a deflationary approach will not suffice, and the problem must be solved independently on each manifold. We propose and solve an optimization problem parametrized by the rank of the minimax center. The solution is computed using a subgradient algorithm on the dual. By scaling the objective and penalizing the information lost by the rank-$k$ minimax center, we jointly recover an optimal dimension, $k^*$, and a central subspace, $U^* \in$ Gr$(k^*,n)$ at the center of the minimum enclosing ball, that best represents the data.

Proceedings of the third "international Traveling Workshop on Interactions between Sparse models and Technology"

The third edition of the "international - Traveling Workshop on Interactions between Sparse models and Technology" (iTWIST) took place in Aalborg, the 4th largest city in Denmark situated beautifully in the northern part of the country, from the 24th to 26th of August 2016. The workshop venue was at the Aalborg University campus. One implicit objective of this biennial workshop is to foster collaboration between international scientific teams by disseminating ideas through both specific oral/poster presentations and free discussions. For this third edition, iTWIST'16 gathered about 50 international participants and features 8 invited talks, 12 oral presentations, and 12 posters on the following themes, all related to the theory, application and generalization of the "sparsity paradigm": Sparsity-driven data sensing and processing (e.g., optics, computer vision, genomics, biomedical, digital communication, channel estimation, astronomy); Application of sparse models in non-convex/non-linear inverse problems (e.g., phase retrieval, blind deconvolution, self calibration); Approximate probabilistic inference for sparse problems; Sparse machine learning and inference; "Blind" inverse problems and dictionary learning; Optimization for sparse modelling; Information theory, geometry and randomness; Sparsity? What's next? (Discrete-valued signals; Union of low-dimensional spaces, Cosparsity, mixed/group norm, model-based, low-complexity models, ...); Matrix/manifold sensing/processing (graph, low-rank approximation, ...); Complexity/accuracy tradeoffs in numerical methods/optimization; Electronic/optical compressive sensors (hardware).

Proceedings of the second "international Traveling Workshop on Interactions between Sparse models and Technology" (iTWIST'14)

The implicit objective of the biennial "international - Traveling Workshop on Interactions between Sparse models and Technology" (iTWIST) is to foster collaboration between international scientific teams by disseminating ideas through both specific oral/poster presentations and free discussions. For its second edition, the iTWIST workshop took place in the medieval and picturesque town of Namur in Belgium, from Wednesday August 27th till Friday August 29th, 2014. The workshop was conveniently located in "The Arsenal" building within walking distance of both hotels and town center. iTWIST'14 has gathered about 70 international participants and has featured 9 invited talks, 10 oral presentations, and 14 posters on the following themes, all related to the theory, application and generalization of the "sparsity paradigm": Sparsity-driven data sensing and processing; Union of low dimensional subspaces; Beyond linear and convex inverse problem; Matrix/manifold/graph sensing/processing; Blind inverse problems and dictionary learning; Sparsity and computational neuroscience; Information theory, geometry and randomness; Complexity/accuracy tradeoffs in numerical methods; Sparsity? What's next?; Sparse machine learning and inference.

Manopt, a Matlab toolbox for optimization on manifolds

Optimization on manifolds is a rapidly developing branch of nonlinear optimization. Its focus is on problems where the smooth geometry of the search space can be leveraged to design efficient numerical algorithms. In particular, optimization on manifolds is well-suited to deal with rank and orthogonality constraints. Such structured constraints appear pervasively in machine learning applications, including low-rank matrix completion, sensor network localization, camera network registration, independent component analysis, metric learning, dimensionality reduction and so on. The Manopt toolbox, available at www.manopt.org, is a user-friendly, documented piece of software dedicated to simplify experimenting with state of the art Riemannian optimization algorithms. We aim particularly at reaching practitioners outside our field.