Synchronization on circles and spheres with nonlinear interactions

We consider the dynamics of $n$ points on a sphere in $\mathbb{R}^d$ ($d \geq 2$) which attract each other according to a function $\varphi$ of their inner products. When $\varphi$ is linear ($\varphi(t) = t$), the points converge to a common value (i.e., synchronize) in various connectivity scenarios: this is part of classical work on Kuramoto oscillator networks. When $\varphi$ is exponential ($\varphi(t) = e^{\beta t}$), these dynamics correspond to a limit of how idealized transformers process data, as described by Geshkovski et al. (2024). Accordingly, they ask whether synchronization occurs for exponential $\varphi$. In the context of consensus for multi-agent control, Markdahl et al. (2018) show that for $d \geq 3$ (spheres), if the interaction graph is connected and $\varphi$ is increasing and convex, then the system synchronizes. What is the situation on circles ($d=2$)? First, we show that $\varphi$ being increasing and convex is no longer sufficient. Then we identify a new condition (that the Taylor coefficients of $\varphi'$ are decreasing) under which we do have synchronization on the circle. In so doing, we provide some answers to the open problems posed by Geshkovski et al. (2024).

Efficiently escaping saddle points on manifolds

Smooth, non-convex optimization problems on Riemannian manifolds occur in machine learning as a result of orthonormality, rank or positivity constraints. First- and second-order necessary optimality conditions state that the Riemannian gradient must be zero, and the Riemannian Hessian must be positive semidefinite. Generalizing Jin et al.'s recent work on perturbed gradient descent (PGD) for optimization on linear spaces [How to Escape Saddle Points Efficiently (2017), Stochastic Gradient Descent Escapes Saddle Points Efficiently (2019)], we propose a version of perturbed Riemannian gradient descent (PRGD) to show that necessary optimality conditions can be met approximately with high probability, without evaluating the Hessian. Specifically, for an arbitrary Riemannian manifold $\mathcal{M}$ of dimension $d$, a sufficiently smooth (possibly non-convex) objective function $f$, and under weak conditions on the retraction chosen to move on the manifold, with high probability, our version of PRGD produces a point with gradient smaller than $\epsilon$ and Hessian within $\sqrt{\epsilon}$ of being positive semidefinite in $O((\log{d})^4 / \epsilon^{2})$ gradient queries. This matches the complexity of PGD in the Euclidean case. Crucially, the dependence on dimension is low. This matters for large-scale applications including PCA and low-rank matrix completion, which both admit natural formulations on manifolds. The key technical idea is to generalize PRGD with a distinction between two types of gradient steps: "steps on the manifold" and "perturbed steps in a tangent space of the manifold." Ultimately, this distinction makes it possible to extend Jin et al.'s analysis seamlessly.

Smoothed analysis of the low-rank approach for smooth semidefinite programs

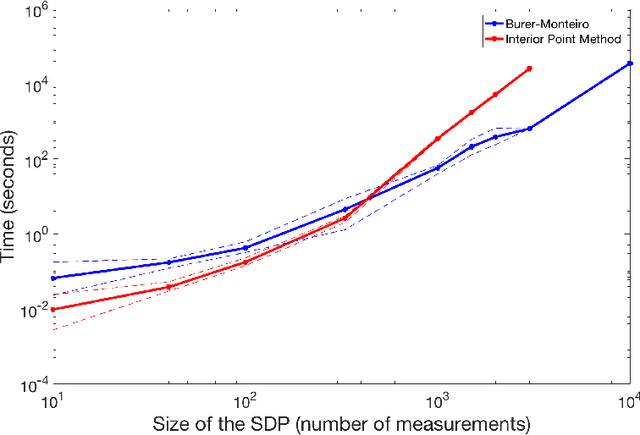
We consider semidefinite programs (SDPs) of size n with equality constraints. In order to overcome scalability issues, Burer and Monteiro proposed a factorized approach based on optimizing over a matrix Y of size $n$ by $k$ such that $X = YY^*$ is the SDP variable. The advantages of such formulation are twofold: the dimension of the optimization variable is reduced and positive semidefiniteness is naturally enforced. However, the problem in Y is non-convex. In prior work, it has been shown that, when the constraints on the factorized variable regularly define a smooth manifold, provided k is large enough, for almost all cost matrices, all second-order stationary points (SOSPs) are optimal. Importantly, in practice, one can only compute points which approximately satisfy necessary optimality conditions, leading to the question: are such points also approximately optimal? To this end, and under similar assumptions, we use smoothed analysis to show that approximate SOSPs for a randomly perturbed objective function are approximate global optima, with k scaling like the square root of the number of constraints (up to log factors). We particularize our results to an SDP relaxation of phase retrieval.

Smoothed analysis for low-rank solutions to semidefinite programs in quadratic penalty form

Semidefinite programs (SDP) are important in learning and combinatorial optimization with numerous applications. In pursuit of low-rank solutions and low complexity algorithms, we consider the Burer--Monteiro factorization approach for solving SDPs. We show that all approximate local optima are global optima for the penalty formulation of appropriately rank-constrained SDPs as long as the number of constraints scales sub-quadratically with the desired rank of the optimal solution. Our result is based on a simple penalty function formulation of the rank-constrained SDP along with a smoothed analysis to avoid worst-case cost matrices. We particularize our results to two applications, namely, Max-Cut and matrix completion.

A Riemannian low-rank method for optimization over semidefinite matrices with block-diagonal constraints

We propose a new algorithm to solve optimization problems of the form $\min f(X)$ for a smooth function $f$ under the constraints that $X$ is positive semidefinite and the diagonal blocks of $X$ are small identity matrices. Such problems often arise as the result of relaxing a rank constraint (lifting). In particular, many estimation tasks involving phases, rotations, orthonormal bases or permutations fit in this framework, and so do certain relaxations of combinatorial problems such as Max-Cut. The proposed algorithm exploits the facts that (1) such formulations admit low-rank solutions, and (2) their rank-restricted versions are smooth optimization problems on a Riemannian manifold. Combining insights from both the Riemannian and the convex geometries of the problem, we characterize when second-order critical points of the smooth problem reveal KKT points of the semidefinite problem. We compare against state of the art, mature software and find that, on certain interesting problem instances, what we call the staircase method is orders of magnitude faster, is more accurate and scales better. Code is available.

Manopt, a Matlab toolbox for optimization on manifolds

Optimization on manifolds is a rapidly developing branch of nonlinear optimization. Its focus is on problems where the smooth geometry of the search space can be leveraged to design efficient numerical algorithms. In particular, optimization on manifolds is well-suited to deal with rank and orthogonality constraints. Such structured constraints appear pervasively in machine learning applications, including low-rank matrix completion, sensor network localization, camera network registration, independent component analysis, metric learning, dimensionality reduction and so on. The Manopt toolbox, available at www.manopt.org, is a user-friendly, documented piece of software dedicated to simplify experimenting with state of the art Riemannian optimization algorithms. We aim particularly at reaching practitioners outside our field.