Geometric statistics with subspace structure preservation for SPD matrices

We present a geometric framework for the processing of SPD-valued data that preserves subspace structures and is based on the efficient computation of extreme generalized eigenvalues. This is achieved through the use of the Thompson geometry of the semidefinite cone. We explore a particular geodesic space structure in detail and establish several properties associated with it. Finally, we review a novel inductive mean of SPD matrices based on this geometry.

Excitable crawling

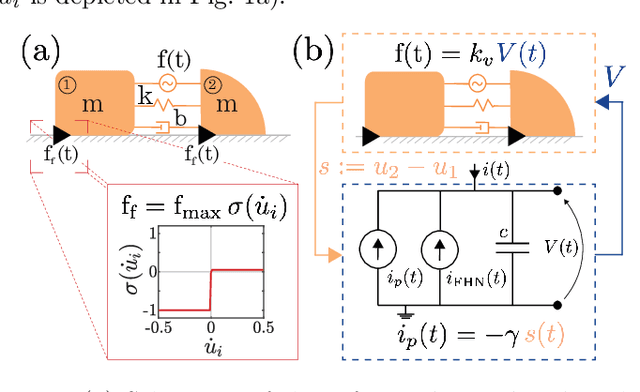
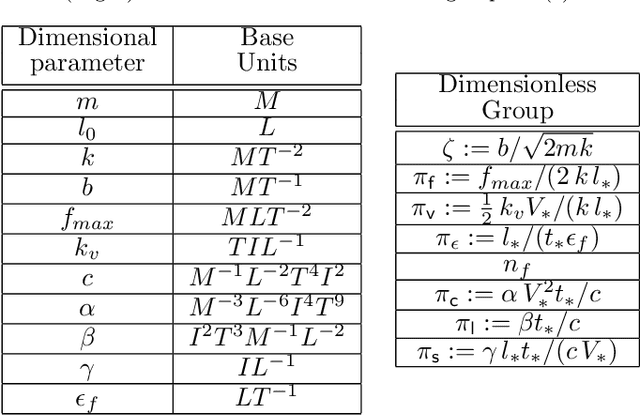
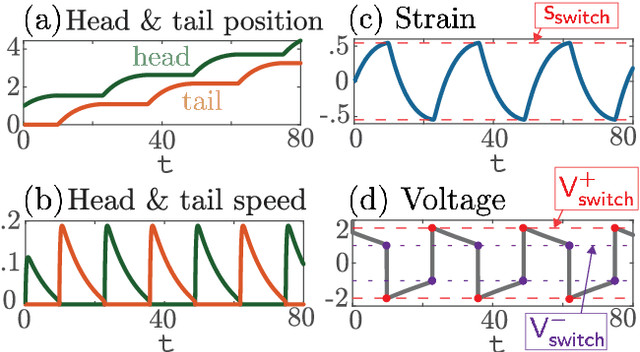
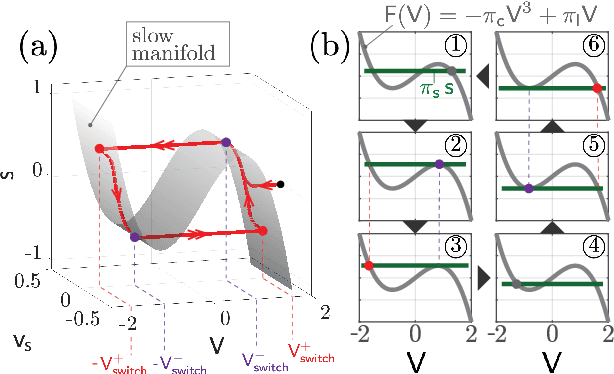
We propose and analyze the suitability of a spiking controller to engineer the locomotion of a soft robotic crawler. Inspired by the FitzHugh-Nagumo model of neural excitability, we design a bistable controller with an electrical flipflop circuit representation capable of generating spikes on-demand when coupled to the passive crawler mechanics. A proprioceptive sensory signal from the crawler mechanics turns bistability of the controller into a rhythmic spiking. The output voltage, in turn, activates the crawler's actuators to generate movement through peristaltic waves. We show through geometric analysis that this control strategy achieves endogenous crawling. The electro-mechanical sensorimotor interconnection provides embodied negative feedback regulation, facilitating locomotion. Dimensional analysis provides insights on the characteristic scales in the crawler's mechanical and electrical dynamics, and how they determine the crawling gait. Adaptive control of the electrical scales to optimally match the mechanical scales can be envisioned to achieve further efficiency, as in homeostatic regulation of neuronal circuits. Our approach can scale up to multiple sensorimotor loops inspired by biological central pattern generators.

Differential geometry with extreme eigenvalues in the positive semidefinite cone

Differential geometric approaches to the analysis and processing of data in the form of symmetric positive definite (SPD) matrices have had notable successful applications to numerous fields including computer vision, medical imaging, and machine learning. The dominant geometric paradigm for such applications has consisted of a few Riemannian geometries associated with spectral computations that are costly at high scale and in high dimensions. We present a route to a scalable geometric framework for the analysis and processing of SPD-valued data based on the efficient computation of extreme generalized eigenvalues through the Hilbert and Thompson geometries of the semidefinite cone. We explore a particular geodesic space structure based on Thompson geometry in detail and establish several properties associated with this structure. Furthermore, we define a novel iterative mean of SPD matrices based on this geometry and prove its existence and uniqueness for a given finite collection of points. Finally, we state and prove a number of desirable properties that are satisfied by this mean.

Reliability of Event Timing in Silicon Neurons

Analog, low-voltage electronics show great promise in producing silicon neurons (SiNs) with unprecedented levels of energy efficiency. Yet, their inherently high susceptibility to process, voltage and temperature (PVT) variations, and noise has long been recognised as a major bottleneck in developing effective neuromorphic solutions. Inspired by spike transmission studies in biophysical, neocortical neurons, we demonstrate that the inherent noise and variability can coexist with reliable spike transmission in analog SiNs, similarly to biological neurons. We illustrate this property on a recent neuromorphic model of a bursting neuron by showcasing three different relevant types of reliable event transmission: single spike transmission, burst transmission, and the on-off control of a half-centre oscillator (HCO) network.

System identification of biophysical neuronal models

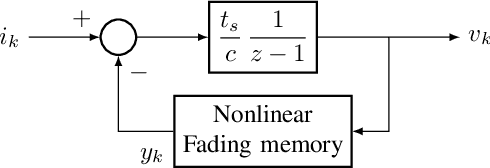
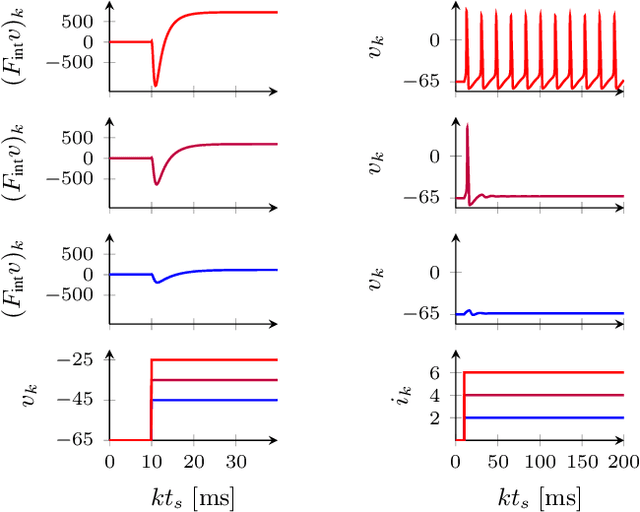
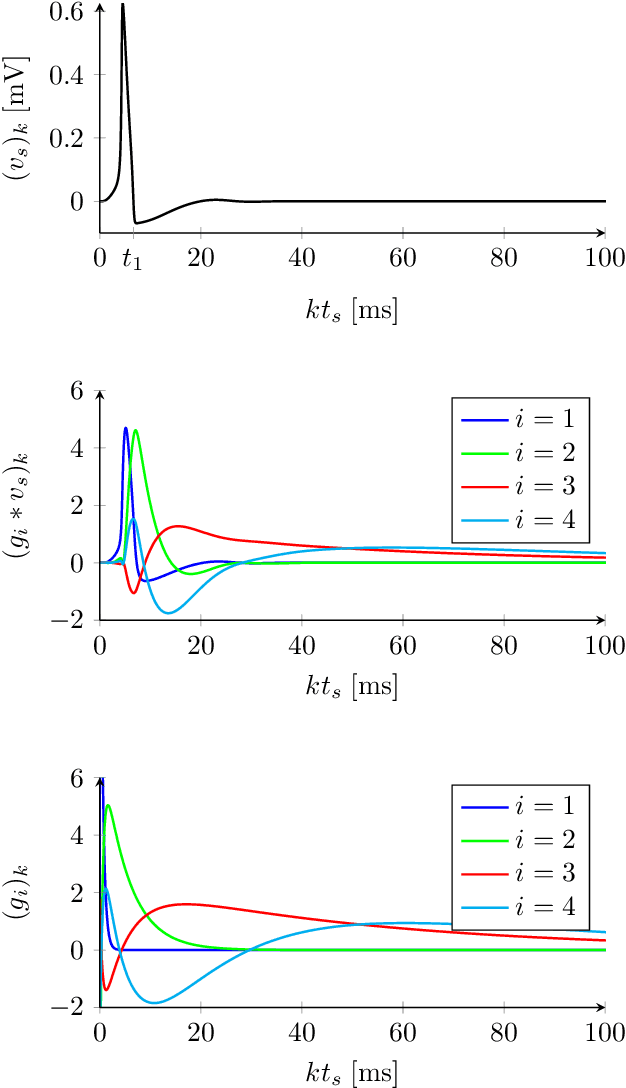
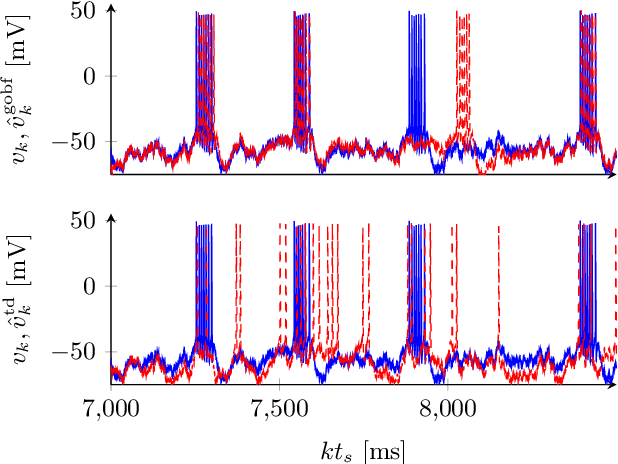
After sixty years of quantitative biophysical modeling of neurons, the identification of neuronal dynamics from input-output data remains a challenging problem, primarily due to the inherently nonlinear nature of excitable behaviors. By reformulating the problem in terms of the identification of an operator with fading memory, we explore a simple approach based on a parametrization given by a series interconnection of Generalized Orthonormal Basis Functions (GOBFs) and static Artificial Neural Networks. We show that GOBFs are particularly well-suited to tackle the identification problem, and provide a heuristic for selecting GOBF poles which addresses the ultra-sensitivity of neuronal behaviors. The method is illustrated on the identification of a bursting model from the crab stomatogastric ganglion.

Inductive Geometric Matrix Midranges

Covariance data as represented by symmetric positive definite (SPD) matrices are ubiquitous throughout technical study as efficient descriptors of interdependent systems. Euclidean analysis of SPD matrices, while computationally fast, can lead to skewed and even unphysical interpretations of data. Riemannian methods preserve the geometric structure of SPD data at the cost of expensive eigenvalue computations. In this paper, we propose a geometric method for unsupervised clustering of SPD data based on the Thompson metric. This technique relies upon a novel "inductive midrange" centroid computation for SPD data, whose properties are examined and numerically confirmed. We demonstrate the incorporation of the Thompson metric and inductive midrange into X-means and K-means++ clustering algorithms.

Scaled stochastic gradient descent for low-rank matrix completion

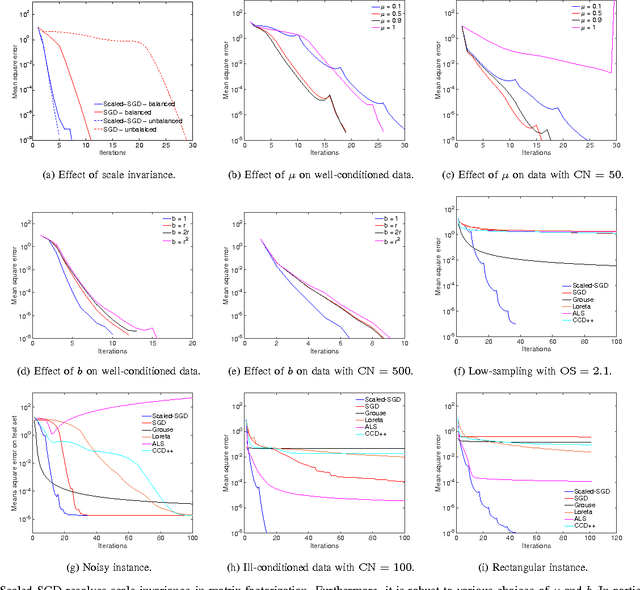
The paper looks at a scaled variant of the stochastic gradient descent algorithm for the matrix completion problem. Specifically, we propose a novel matrix-scaling of the partial derivatives that acts as an efficient preconditioning for the standard stochastic gradient descent algorithm. This proposed matrix-scaling provides a trade-off between local and global second order information. It also resolves the issue of scale invariance that exists in matrix factorization models. The overall computational complexity is linear with the number of known entries, thereby extending to a large-scale setup. Numerical comparisons show that the proposed algorithm competes favorably with state-of-the-art algorithms on various different benchmarks.

On the Projective Geometry of Kalman Filter

Convergence of the Kalman filter is best analyzed by studying the contraction of the Riccati map in the space of positive definite (covariance) matrices. In this paper, we explore how this contraction property relates to a more fundamental non-expansiveness property of filtering maps in the space of probability distributions endowed with the Hilbert metric. This is viewed as a preliminary step towards improving the convergence analysis of filtering algorithms over general graphical models.

Sparse plus low-rank autoregressive identification in neuroimaging time series

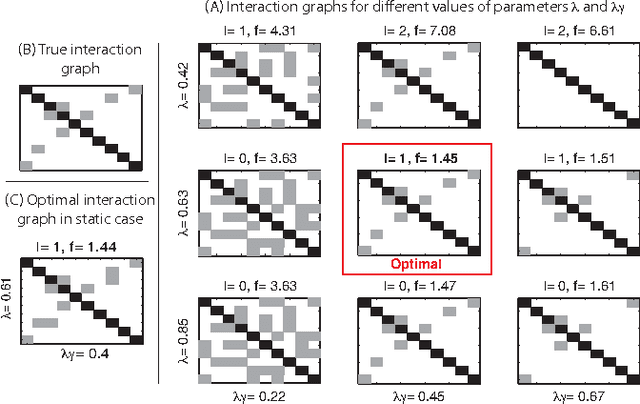
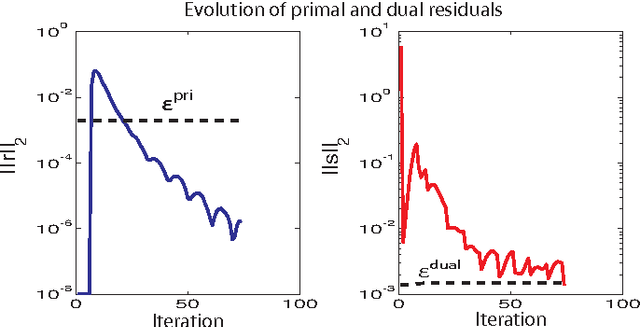
This paper considers the problem of identifying multivariate autoregressive (AR) sparse plus low-rank graphical models. Based on the corresponding problem formulation recently presented, we use the alternating direction method of multipliers (ADMM) to efficiently solve it and scale it to sizes encountered in neuroimaging applications. We apply this decomposition on synthetic and real neuroimaging datasets with a specific focus on the information encoded in the low-rank structure of our model. In particular, we illustrate that this information captures the spatio-temporal structure of the original data, generalizing classical component analysis approaches.

Manopt, a Matlab toolbox for optimization on manifolds

Optimization on manifolds is a rapidly developing branch of nonlinear optimization. Its focus is on problems where the smooth geometry of the search space can be leveraged to design efficient numerical algorithms. In particular, optimization on manifolds is well-suited to deal with rank and orthogonality constraints. Such structured constraints appear pervasively in machine learning applications, including low-rank matrix completion, sensor network localization, camera network registration, independent component analysis, metric learning, dimensionality reduction and so on. The Manopt toolbox, available at www.manopt.org, is a user-friendly, documented piece of software dedicated to simplify experimenting with state of the art Riemannian optimization algorithms. We aim particularly at reaching practitioners outside our field.