Geometric statistics with subspace structure preservation for SPD matrices

We present a geometric framework for the processing of SPD-valued data that preserves subspace structures and is based on the efficient computation of extreme generalized eigenvalues. This is achieved through the use of the Thompson geometry of the semidefinite cone. We explore a particular geodesic space structure in detail and establish several properties associated with it. Finally, we review a novel inductive mean of SPD matrices based on this geometry.

Invariant kernels on Riemannian symmetric spaces: a harmonic-analytic approach

This work aims to prove that the classical Gaussian kernel, when defined on a non-Euclidean symmetric space, is never positive-definite for any choice of parameter. To achieve this goal, the paper develops new geometric and analytical arguments. These provide a rigorous characterization of the positive-definiteness of the Gaussian kernel, which is complete but for a limited number of scenarios in low dimensions that are treated by numerical computations. Chief among these results are the L$^{\!\scriptscriptstyle p}$-$\hspace{0.02cm}$Godement theorems (where $p = 1,2$), which provide verifiable necessary and sufficient conditions for a kernel defined on a symmetric space of non-compact type to be positive-definite. A celebrated theorem, sometimes called the Bochner-Godement theorem, already gives such conditions and is far more general in its scope, but is especially hard to apply. Beyond the connection with the Gaussian kernel, the new results in this work lay out a blueprint for the study of invariant kernels on symmetric spaces, bringing forth specific harmonic analysis tools that suggest many future applications.

Geometric Learning with Positively Decomposable Kernels

Kernel methods are powerful tools in machine learning. Classical kernel methods are based on positive-definite kernels, which map data spaces into reproducing kernel Hilbert spaces (RKHS). For non-Euclidean data spaces, positive-definite kernels are difficult to come by. In this case, we propose the use of reproducing kernel Krein space (RKKS) based methods, which require only kernels that admit a positive decomposition. We show that one does not need to access this decomposition in order to learn in RKKS. We then investigate the conditions under which a kernel is positively decomposable. We show that invariant kernels admit a positive decomposition on homogeneous spaces under tractable regularity assumptions. This makes them much easier to construct than positive-definite kernels, providing a route for learning with kernels for non-Euclidean data. By the same token, this provides theoretical foundations for RKKS-based methods in general.

Differential geometry with extreme eigenvalues in the positive semidefinite cone

Differential geometric approaches to the analysis and processing of data in the form of symmetric positive definite (SPD) matrices have had notable successful applications to numerous fields including computer vision, medical imaging, and machine learning. The dominant geometric paradigm for such applications has consisted of a few Riemannian geometries associated with spectral computations that are costly at high scale and in high dimensions. We present a route to a scalable geometric framework for the analysis and processing of SPD-valued data based on the efficient computation of extreme generalized eigenvalues through the Hilbert and Thompson geometries of the semidefinite cone. We explore a particular geodesic space structure based on Thompson geometry in detail and establish several properties associated with this structure. Furthermore, we define a novel iterative mean of SPD matrices based on this geometry and prove its existence and uniqueness for a given finite collection of points. Finally, we state and prove a number of desirable properties that are satisfied by this mean.

The Gaussian kernel on the circle and spaces that admit isometric embeddings of the circle

On Euclidean spaces, the Gaussian kernel is one of the most widely used kernels in applications. It has also been used on non-Euclidean spaces, where it is known that there may be (and often are) scale parameters for which it is not positive definite. Hope remains that this kernel is positive definite for many choices of parameter. However, we show that the Gaussian kernel is not positive definite on the circle for any choice of parameter. This implies that on metric spaces in which the circle can be isometrically embedded, such as spheres, projective spaces and Grassmannians, the Gaussian kernel is not positive definite for any parameter.

Geometric Learning of Hidden Markov Models via a Method of Moments Algorithm

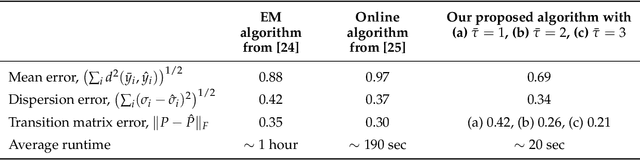
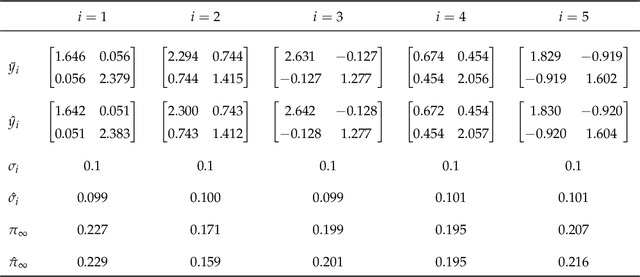
We present a novel algorithm for learning the parameters of hidden Markov models (HMMs) in a geometric setting where the observations take values in Riemannian manifolds. In particular, we elevate a recent second-order method of moments algorithm that incorporates non-consecutive correlations to a more general setting where observations take place in a Riemannian symmetric space of non-positive curvature and the observation likelihoods are Riemannian Gaussians. The resulting algorithm decouples into a Riemannian Gaussian mixture model estimation algorithm followed by a sequence of convex optimization procedures. We demonstrate through examples that the learner can result in significantly improved speed and numerical accuracy compared to existing learners.

Riemannian statistics meets random matrix theory: towards learning from high-dimensional covariance matrices

Riemannian Gaussian distributions were initially introduced as basic building blocks for learning models which aim to capture the intrinsic structure of statistical populations of positive-definite matrices (here called covariance matrices). While the potential applications of such models have attracted significant attention, a major obstacle still stands in the way of these applications: there seems to exist no practical method of computing the normalising factors associated with Riemannian Gaussian distributions on spaces of high-dimensional covariance matrices. The present paper shows that this missing method comes from an unexpected new connection with random matrix theory. Its main contribution is to prove that Riemannian Gaussian distributions of real, complex, or quaternion covariance matrices are equivalent to orthogonal, unitary, or symplectic log-normal matrix ensembles. This equivalence yields a highly efficient approximation of the normalising factors, in terms of a rather simple analytic expression. The error due to this approximation decreases like the inverse square of dimension. Numerical experiments are conducted which demonstrate how this new approximation can unlock the difficulties which have impeded applications to real-world datasets of high-dimensional covariance matrices. The paper then turns to Riemannian Gaussian distributions of block-Toeplitz covariance matrices. These are equivalent to yet another kind of random matrix ensembles, here called "acosh-normal" ensembles. Orthogonal and unitary "acosh-normal" ensembles correspond to the cases of block-Toeplitz with Toeplitz blocks, and block-Toeplitz (with general blocks) covariance matrices, respectively.

Online learning of Riemannian hidden Markov models in homogeneous Hadamard spaces

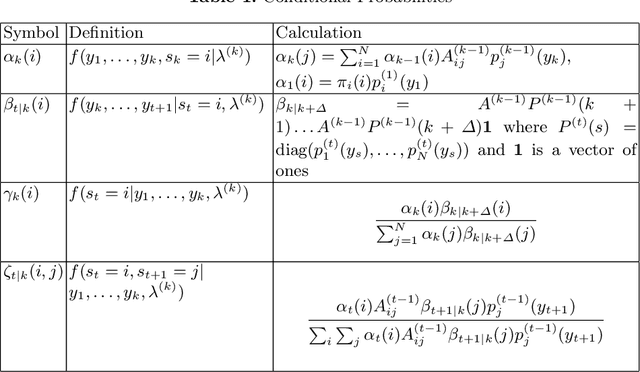
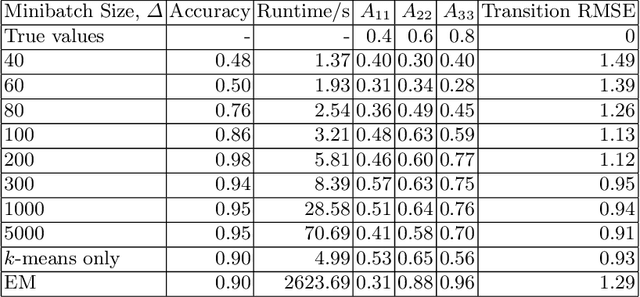
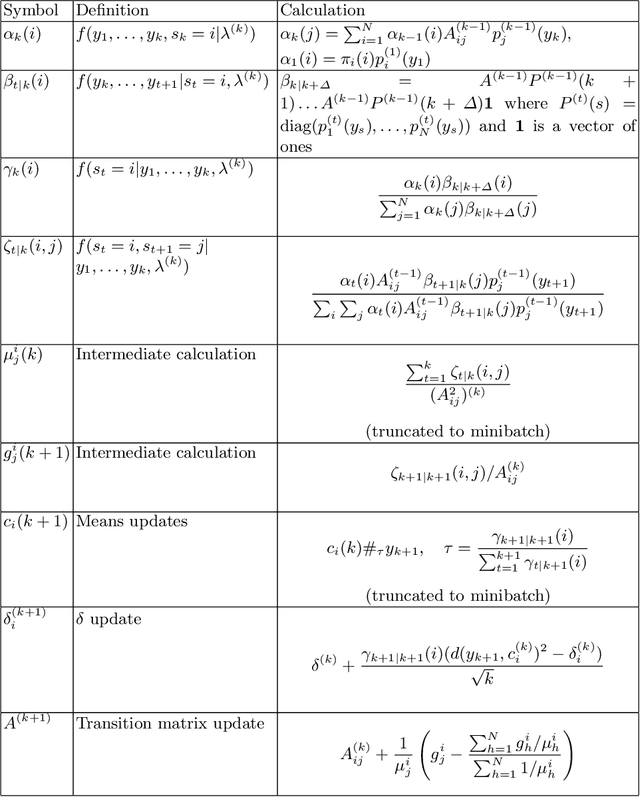
Hidden Markov models with observations in a Euclidean space play an important role in signal and image processing. Previous work extending to models where observations lie in Riemannian manifolds based on the Baum-Welch algorithm suffered from high memory usage and slow speed. Here we present an algorithm that is online, more accurate, and offers dramatic improvements in speed and efficiency.

Inductive Geometric Matrix Midranges

Covariance data as represented by symmetric positive definite (SPD) matrices are ubiquitous throughout technical study as efficient descriptors of interdependent systems. Euclidean analysis of SPD matrices, while computationally fast, can lead to skewed and even unphysical interpretations of data. Riemannian methods preserve the geometric structure of SPD data at the cost of expensive eigenvalue computations. In this paper, we propose a geometric method for unsupervised clustering of SPD data based on the Thompson metric. This technique relies upon a novel "inductive midrange" centroid computation for SPD data, whose properties are examined and numerically confirmed. We demonstrate the incorporation of the Thompson metric and inductive midrange into X-means and K-means++ clustering algorithms.