Invariant kernels on Riemannian symmetric spaces: a harmonic-analytic approach

This work aims to prove that the classical Gaussian kernel, when defined on a non-Euclidean symmetric space, is never positive-definite for any choice of parameter. To achieve this goal, the paper develops new geometric and analytical arguments. These provide a rigorous characterization of the positive-definiteness of the Gaussian kernel, which is complete but for a limited number of scenarios in low dimensions that are treated by numerical computations. Chief among these results are the L$^{\!\scriptscriptstyle p}$-$\hspace{0.02cm}$Godement theorems (where $p = 1,2$), which provide verifiable necessary and sufficient conditions for a kernel defined on a symmetric space of non-compact type to be positive-definite. A celebrated theorem, sometimes called the Bochner-Godement theorem, already gives such conditions and is far more general in its scope, but is especially hard to apply. Beyond the connection with the Gaussian kernel, the new results in this work lay out a blueprint for the study of invariant kernels on symmetric spaces, bringing forth specific harmonic analysis tools that suggest many future applications.

Geometric Learning with Positively Decomposable Kernels

Kernel methods are powerful tools in machine learning. Classical kernel methods are based on positive-definite kernels, which map data spaces into reproducing kernel Hilbert spaces (RKHS). For non-Euclidean data spaces, positive-definite kernels are difficult to come by. In this case, we propose the use of reproducing kernel Krein space (RKKS) based methods, which require only kernels that admit a positive decomposition. We show that one does not need to access this decomposition in order to learn in RKKS. We then investigate the conditions under which a kernel is positively decomposable. We show that invariant kernels admit a positive decomposition on homogeneous spaces under tractable regularity assumptions. This makes them much easier to construct than positive-definite kernels, providing a route for learning with kernels for non-Euclidean data. By the same token, this provides theoretical foundations for RKKS-based methods in general.

Geometric Learning of Hidden Markov Models via a Method of Moments Algorithm

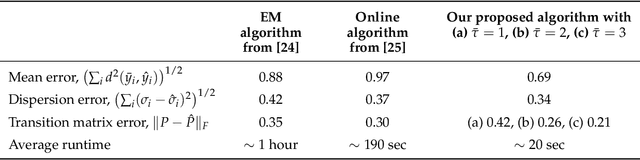
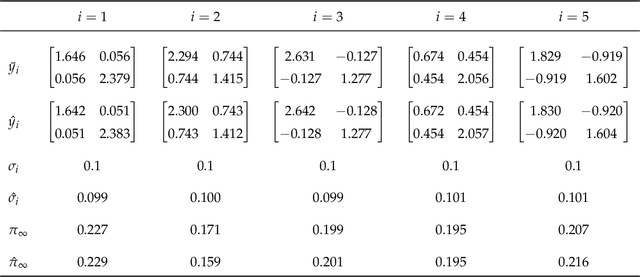
We present a novel algorithm for learning the parameters of hidden Markov models (HMMs) in a geometric setting where the observations take values in Riemannian manifolds. In particular, we elevate a recent second-order method of moments algorithm that incorporates non-consecutive correlations to a more general setting where observations take place in a Riemannian symmetric space of non-positive curvature and the observation likelihoods are Riemannian Gaussians. The resulting algorithm decouples into a Riemannian Gaussian mixture model estimation algorithm followed by a sequence of convex optimization procedures. We demonstrate through examples that the learner can result in significantly improved speed and numerical accuracy compared to existing learners.

Riemannian statistics meets random matrix theory: towards learning from high-dimensional covariance matrices

Riemannian Gaussian distributions were initially introduced as basic building blocks for learning models which aim to capture the intrinsic structure of statistical populations of positive-definite matrices (here called covariance matrices). While the potential applications of such models have attracted significant attention, a major obstacle still stands in the way of these applications: there seems to exist no practical method of computing the normalising factors associated with Riemannian Gaussian distributions on spaces of high-dimensional covariance matrices. The present paper shows that this missing method comes from an unexpected new connection with random matrix theory. Its main contribution is to prove that Riemannian Gaussian distributions of real, complex, or quaternion covariance matrices are equivalent to orthogonal, unitary, or symplectic log-normal matrix ensembles. This equivalence yields a highly efficient approximation of the normalising factors, in terms of a rather simple analytic expression. The error due to this approximation decreases like the inverse square of dimension. Numerical experiments are conducted which demonstrate how this new approximation can unlock the difficulties which have impeded applications to real-world datasets of high-dimensional covariance matrices. The paper then turns to Riemannian Gaussian distributions of block-Toeplitz covariance matrices. These are equivalent to yet another kind of random matrix ensembles, here called "acosh-normal" ensembles. Orthogonal and unitary "acosh-normal" ensembles correspond to the cases of block-Toeplitz with Toeplitz blocks, and block-Toeplitz (with general blocks) covariance matrices, respectively.

On Riemannian Stochastic Approximation Schemes with Fixed Step-Size

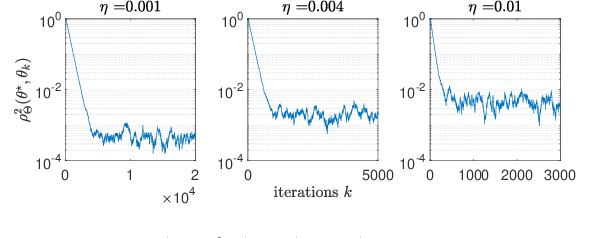
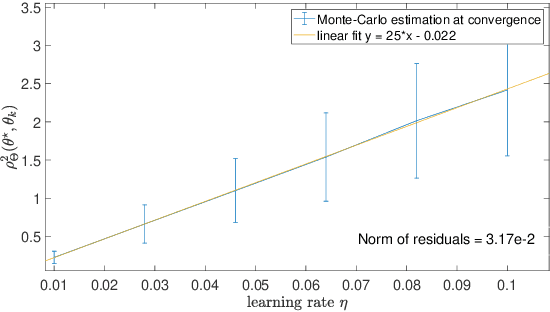
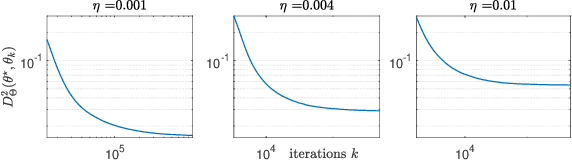
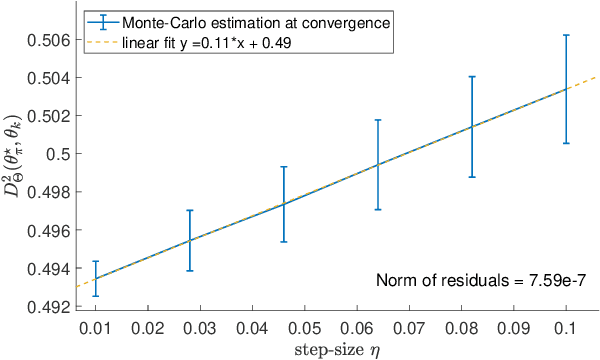
This paper studies fixed step-size stochastic approximation (SA) schemes, including stochastic gradient schemes, in a Riemannian framework. It is motivated by several applications, where geodesics can be computed explicitly, and their use accelerates crude Euclidean methods. A fixed step-size scheme defines a family of time-homogeneous Markov chains, parametrized by the step-size. Here, using this formulation, non-asymptotic performance bounds are derived, under Lyapunov conditions. Then, for any step-size, the corresponding Markov chain is proved to admit a unique stationary distribution, and to be geometrically ergodic. This result gives rise to a family of stationary distributions indexed by the step-size, which is further shown to converge to a Dirac measure, concentrated at the solution of the problem at hand, as the step-size goes to 0. Finally, the asymptotic rate of this convergence is established, through an asymptotic expansion of the bias, and a central limit theorem.

Online learning of Riemannian hidden Markov models in homogeneous Hadamard spaces

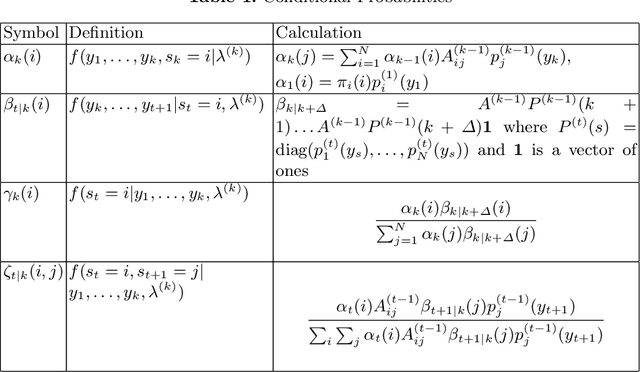
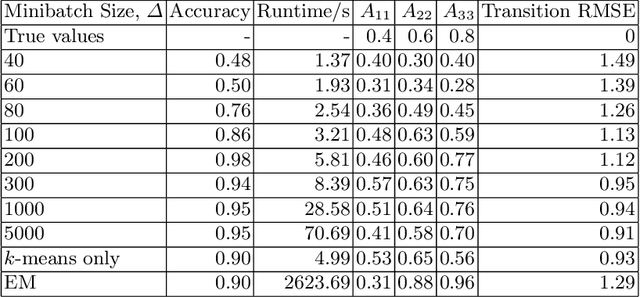
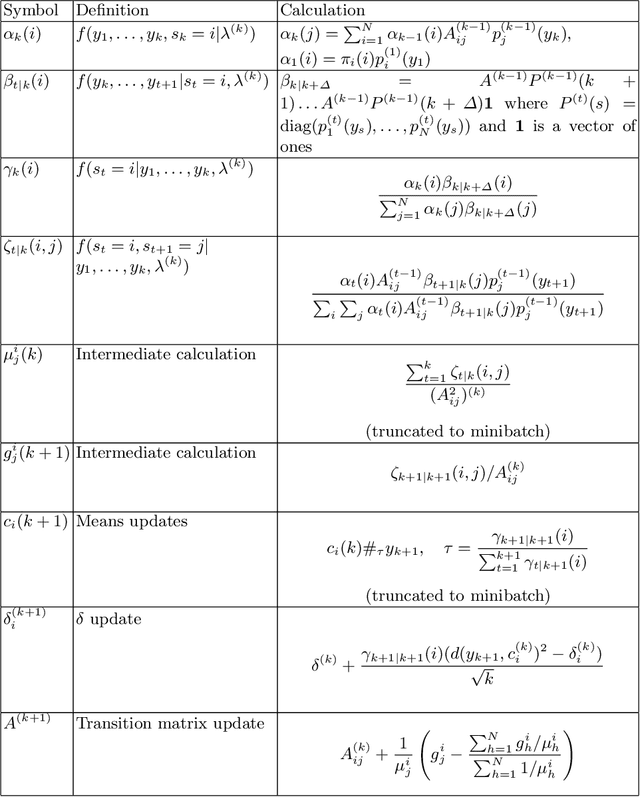
Hidden Markov models with observations in a Euclidean space play an important role in signal and image processing. Previous work extending to models where observations lie in Riemannian manifolds based on the Baum-Welch algorithm suffered from high memory usage and slow speed. Here we present an algorithm that is online, more accurate, and offers dramatic improvements in speed and efficiency.

Convergence Analysis of Riemannian Stochastic Approximation Schemes

This paper analyzes the convergence for a large class of Riemannian stochastic approximation (SA) schemes, which aim at tackling stochastic optimization problems. In particular, the recursions we study use either the exponential map of the considered manifold (geodesic schemes) or more general retraction functions (retraction schemes) used as a proxy for the exponential map. Such approximations are of great interest since they are low complexity alternatives to geodesic schemes. Under the assumption that the mean field of the SA is correlated with the gradient of a smooth Lyapunov function (possibly non-convex), we show that the above Riemannian SA schemes find an ${\mathcal{O}}(b_\infty + \log n / \sqrt{n})$-stationary point (in expectation) within ${\mathcal{O}}(n)$ iterations, where $b_\infty \geq 0$ is the asymptotic bias. Compared to previous works, the conditions we derive are considerably milder. First, all our analysis are global as we do not assume iterates to be a-priori bounded. Second, we study biased SA schemes. To be more specific, we consider the case where the mean-field function can only be estimated up to a small bias, and/or the case in which the samples are drawn from a controlled Markov chain. Third, the conditions on retractions required to ensure convergence of the related SA schemes are weak and hold for well-known examples. We illustrate our results on three machine learning problems.

Riemannian geometry for Compound Gaussian distributions: application to recursive change detection

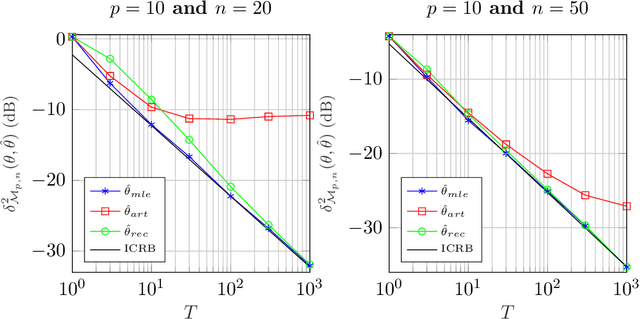
A new Riemannian geometry for the Compound Gaussian distribution is proposed. In particular, the Fisher information metric is obtained, along with corresponding geodesics and distance function. This new geometry is applied on a change detection problem on Multivariate Image Times Series: a recursive approach based on Riemannian optimization is developed. As shown on simulated data, it allows to reach optimal performance while being computationally more efficient.