Random matrix theory improved Fréchet mean of symmetric positive definite matrices

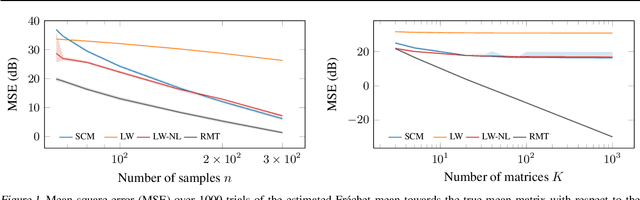
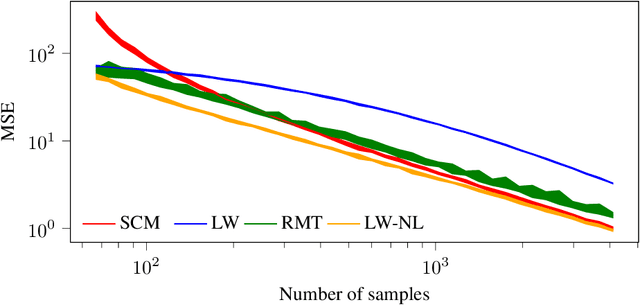
In this study, we consider the realm of covariance matrices in machine learning, particularly focusing on computing Fr\'echet means on the manifold of symmetric positive definite matrices, commonly referred to as Karcher or geometric means. Such means are leveraged in numerous machine-learning tasks. Relying on advanced statistical tools, we introduce a random matrix theory-based method that estimates Fr\'echet means, which is particularly beneficial when dealing with low sample support and a high number of matrices to average. Our experimental evaluation, involving both synthetic and real-world EEG and hyperspectral datasets, shows that we largely outperform state-of-the-art methods.

A New Statistic for Testing Covariance Equality in High-Dimensional Gaussian Low-Rank Models

In this paper, we consider the problem of testing equality of the covariance matrices of L complex Gaussian multivariate time series of dimension $M$ . We study the special case where each of the L covariance matrices is modeled as a rank K perturbation of the identity matrix, corresponding to a signal plus noise model. A new test statistic based on the estimates of the eigenvalues of the different covariance matrices is proposed. In particular, we show that this statistic is consistent and with controlled type I error in the high-dimensional asymptotic regime where the sample sizes $N_1,\ldots,N_L$ of each time series and the dimension $M$ both converge to infinity at the same rate, while $K$ and $L$ are kept fixed. We also provide some simulations on synthetic and real data (SAR images) which demonstrate significant improvements over some classical methods such as the GLRT, or other alternative methods relevant for the high-dimensional regime and the low-rank model.

Natural Bayesian Cramér-Rao Bound with an Application to Covariance Estimation

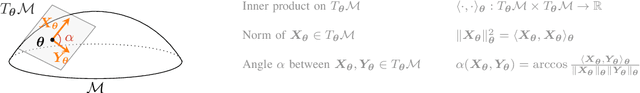
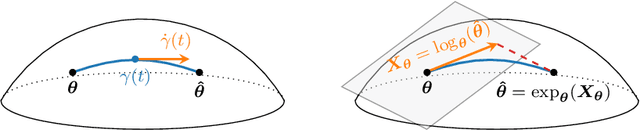
In this paper, we propose to develop a new Cram\'er-Rao Bound (CRB) when the parameter to estimate lies in a manifold and follows a prior distribution. This derivation leads to a natural inequality between an error criteria based on geometrical properties and this new bound. This main contribution is illustrated in the problem of covariance estimation when the data follow a Gaussian distribution and the prior distribution is an inverse Wishart. Numerical simulation shows new results where the proposed CRB allows to exhibit interesting properties of the MAP estimator which are not observed with the classical Bayesian CRB.

The Fisher-Rao geometry of CES distributions

When dealing with a parametric statistical model, a Riemannian manifold can naturally appear by endowing the parameter space with the Fisher information metric. The geometry induced on the parameters by this metric is then referred to as the Fisher-Rao information geometry. Interestingly, this yields a point of view that allows for leveragingmany tools from differential geometry. After a brief introduction about these concepts, we will present some practical uses of these geometric tools in the framework of elliptical distributions. This second part of the exposition is divided into three main axes: Riemannian optimization for covariance matrix estimation, Intrinsic Cram\'er-Rao bounds, and classification using Riemannian distances.

Riemannian optimization for non-centered mixture of scaled Gaussian distributions

This paper studies the statistical model of the non-centered mixture of scaled Gaussian distributions (NC-MSG). Using the Fisher-Rao information geometry associated to this distribution, we derive a Riemannian gradient descent algorithm. This algorithm is leveraged for two minimization problems. The first one is the minimization of a regularized negative log- likelihood (NLL). The latter makes the trade-off between a white Gaussian distribution and the NC-MSG. Conditions on the regularization are given so that the existence of a minimum to this problem is guaranteed without assumptions on the samples. Then, the Kullback-Leibler (KL) divergence between two NC-MSG is derived. This divergence enables us to define a minimization problem to compute centers of mass of several NC-MSGs. The proposed Riemannian gradient descent algorithm is leveraged to solve this second minimization problem. Numerical experiments show the good performance and the speed of the Riemannian gradient descent on the two problems. Finally, a Nearest centroid classifier is implemented leveraging the KL divergence and its associated center of mass. Applied on the large scale dataset Breizhcrops, this classifier shows good accuracies as well as robustness to rigid transformations of the test set.

Robust Geometric Metric Learning

This paper proposes new algorithms for the metric learning problem. We start by noticing that several classical metric learning formulations from the literature can be viewed as modified covariance matrix estimation problems. Leveraging this point of view, a general approach, called Robust Geometric Metric Learning (RGML), is then studied. This method aims at simultaneously estimating the covariance matrix of each class while shrinking them towards their (unknown) barycenter. We focus on two specific costs functions: one associated with the Gaussian likelihood (RGML Gaussian), and one with Tyler's M -estimator (RGML Tyler). In both, the barycenter is defined with the Riemannian distance, which enjoys nice properties of geodesic convexity and affine invariance. The optimization is performed using the Riemannian geometry of symmetric positive definite matrices and its submanifold of unit determinant. Finally, the performance of RGML is asserted on real datasets. Strong performance is exhibited while being robust to mislabeled data.

Robust low-rank covariance matrix estimation with a general pattern of missing values

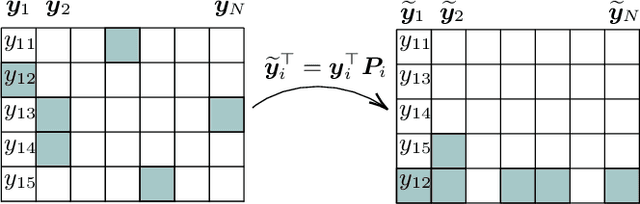
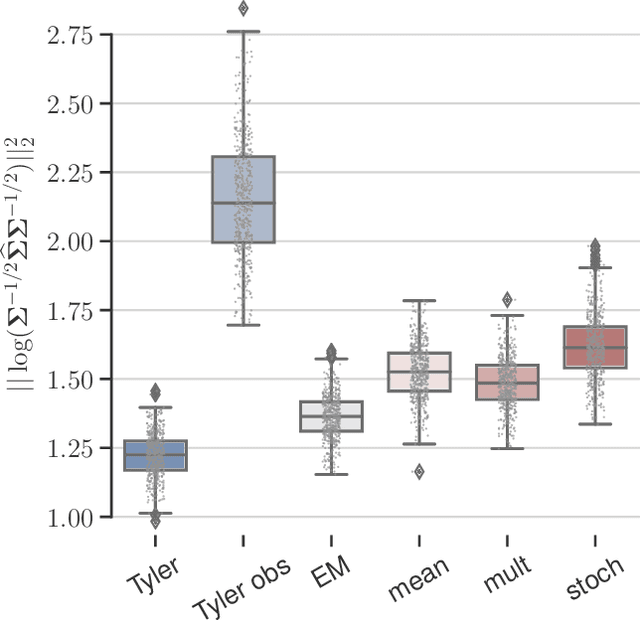
This paper tackles the problem of robust covariance matrix estimation when the data is incomplete. Classical statistical estimation methodologies are usually built upon the Gaussian assumption, whereas existing robust estimation ones assume unstructured signal models. The former can be inaccurate in real-world data sets in which heterogeneity causes heavy-tail distributions, while the latter does not profit from the usual low-rank structure of the signal. Taking advantage of both worlds, a covariance matrix estimation procedure is designed on a robust (compound Gaussian) low-rank model by leveraging the observed-data likelihood function within an expectation-maximization algorithm. It is also designed to handle general pattern of missing values. The proposed procedure is first validated on simulated data sets. Then, its interest for classification and clustering applications is assessed on two real data sets with missing values, which include multispectral and hyperspectral time series.

Riemannian geometry for Compound Gaussian distributions: application to recursive change detection

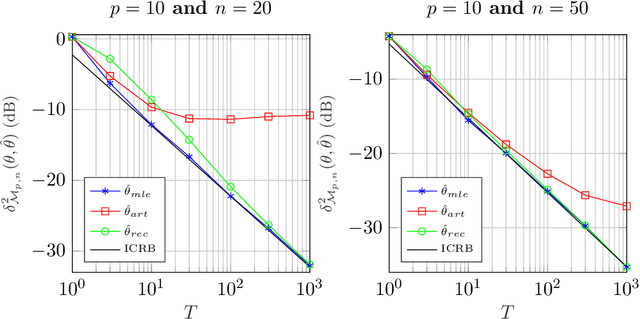
A new Riemannian geometry for the Compound Gaussian distribution is proposed. In particular, the Fisher information metric is obtained, along with corresponding geodesics and distance function. This new geometry is applied on a change detection problem on Multivariate Image Times Series: a recursive approach based on Riemannian optimization is developed. As shown on simulated data, it allows to reach optimal performance while being computationally more efficient.