Natural Bayesian Cramér-Rao Bound with an Application to Covariance Estimation

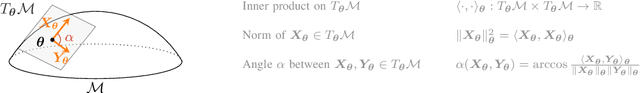
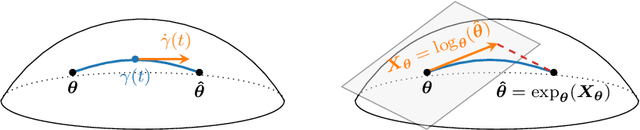
In this paper, we propose to develop a new Cram\'er-Rao Bound (CRB) when the parameter to estimate lies in a manifold and follows a prior distribution. This derivation leads to a natural inequality between an error criteria based on geometrical properties and this new bound. This main contribution is illustrated in the problem of covariance estimation when the data follow a Gaussian distribution and the prior distribution is an inverse Wishart. Numerical simulation shows new results where the proposed CRB allows to exhibit interesting properties of the MAP estimator which are not observed with the classical Bayesian CRB.