Random matrix theory improved Fréchet mean of symmetric positive definite matrices

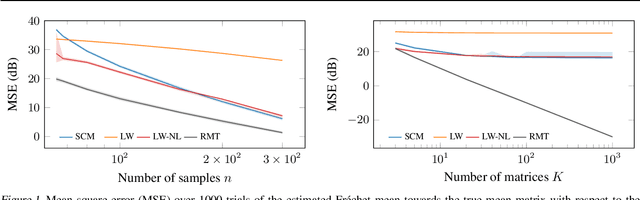
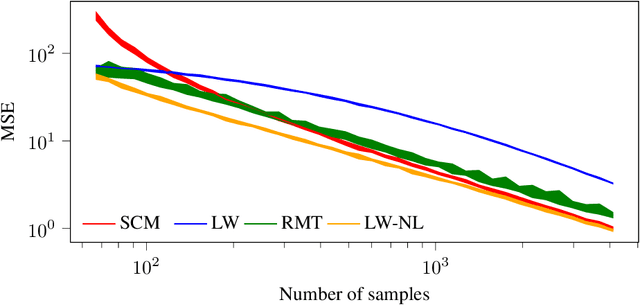
In this study, we consider the realm of covariance matrices in machine learning, particularly focusing on computing Fr\'echet means on the manifold of symmetric positive definite matrices, commonly referred to as Karcher or geometric means. Such means are leveraged in numerous machine-learning tasks. Relying on advanced statistical tools, we introduce a random matrix theory-based method that estimates Fr\'echet means, which is particularly beneficial when dealing with low sample support and a high number of matrices to average. Our experimental evaluation, involving both synthetic and real-world EEG and hyperspectral datasets, shows that we largely outperform state-of-the-art methods.

Riemannian classification of EEG signals with missing values

This paper proposes two strategies to handle missing data for the classification of electroencephalograms using covariance matrices. The first approach estimates the covariance from imputed data with the $k$-nearest neighbors algorithm; the second relies on the observed data by leveraging the observed-data likelihood within an expectation-maximization algorithm. Both approaches are combined with the minimum distance to Riemannian mean classifier and applied to a classification task of event related-potentials, a widely known paradigm of brain-computer interface paradigms. As results show, the proposed strategies perform better than the classification based on observed data and allow to keep a high accuracy even when the missing data ratio increases.

Block-wise Minimization-Majorization algorithm for Huber's criterion: sparse learning and applications

Huber's criterion can be used for robust joint estimation of regression and scale parameters in the linear model. Huber's (Huber, 1981) motivation for introducing the criterion stemmed from non-convexity of the joint maximum likelihood objective function as well as non-robustness (unbounded influence function) of the associated ML-estimate of scale. In this paper, we illustrate how the original algorithm proposed by Huber can be set within the block-wise minimization majorization framework. In addition, we propose novel data-adaptive step sizes for both the location and scale, which are further improving the convergence. We then illustrate how Huber's criterion can be used for sparse learning of underdetermined linear model using the iterative hard thresholding approach. We illustrate the usefulness of the algorithms in an image denoising application and simulation studies.

Riemannian geometry for Compound Gaussian distributions: application to recursive change detection

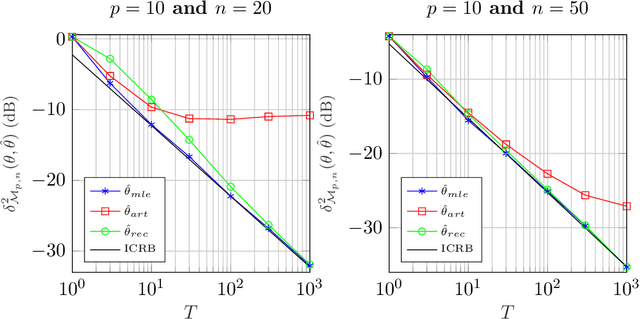
A new Riemannian geometry for the Compound Gaussian distribution is proposed. In particular, the Fisher information metric is obtained, along with corresponding geodesics and distance function. This new geometry is applied on a change detection problem on Multivariate Image Times Series: a recursive approach based on Riemannian optimization is developed. As shown on simulated data, it allows to reach optimal performance while being computationally more efficient.