DeepInverse: A Python package for solving imaging inverse problems with deep learning

DeepInverse is an open-source PyTorch-based library for solving imaging inverse problems. The library covers all crucial steps in image reconstruction from the efficient implementation of forward operators (e.g., optics, MRI, tomography), to the definition and resolution of variational problems and the design and training of advanced neural network architectures. In this paper, we describe the main functionality of the library and discuss the main design choices.

Disentangling Modes and Interference in the Spectrogram of Multicomponent Signals

In this paper, we investigate how the spectrogram of multicomponent signals can be decomposed into a mode part and an interference part. We explore two approaches: (i) a variational method inspired by texture-geometry decomposition in image processing, and (ii) a supervised learning approach using a U-Net architecture, trained on a dataset encompassing diverse interference patterns and noise conditions. Once the interference component is identified, we explain how it enables us to define a criterion to locally adapt the window length used in the definition of the spectrogram, for the sake of improving ridge detection in the presence of close modes. Numerical experiments illustrate the advantages and limitations of both approaches for spectrogram decomposition, highlighting their potential for enhancing time-frequency analysis in the presence of strong interference.

Beyond R-barycenters: an effective averaging method on Stiefel and Grassmann manifolds

In this paper, the issue of averaging data on a manifold is addressed. While the Fr\'echet mean resulting from Riemannian geometry appears ideal, it is unfortunately not always available and often computationally very expensive. To overcome this, R-barycenters have been proposed and successfully applied to Stiefel and Grassmann manifolds. However, R-barycenters still suffer severe limitations as they rely on iterative algorithms and complicated operators. We propose simpler, yet efficient, barycenters that we call RL-barycenters. We show that, in the setting relevant to most applications, our framework yields astonishingly simple barycenters: arithmetic means projected onto the manifold. We apply this approach to the Stiefel and Grassmann manifolds. On simulated data, our approach is competitive with respect to existing averaging methods, while computationally cheaper.

Unsupervised classification of the spectrogram zeros

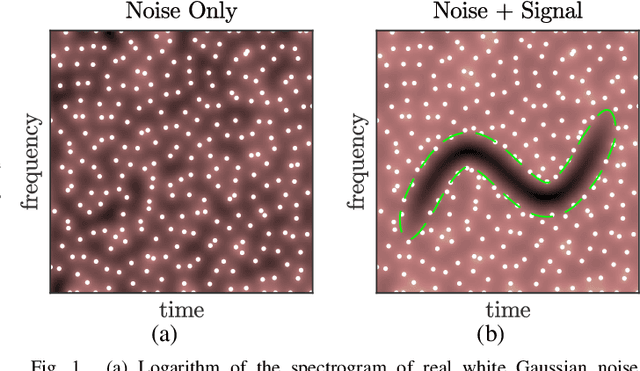
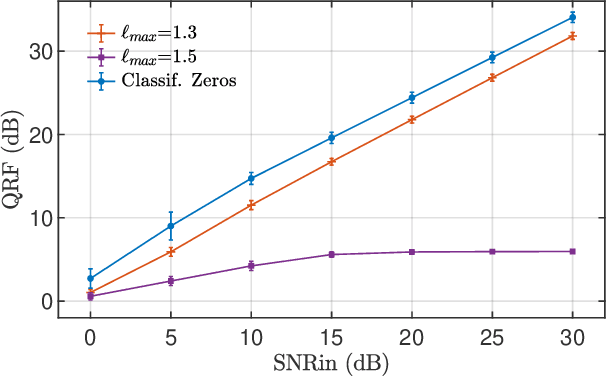
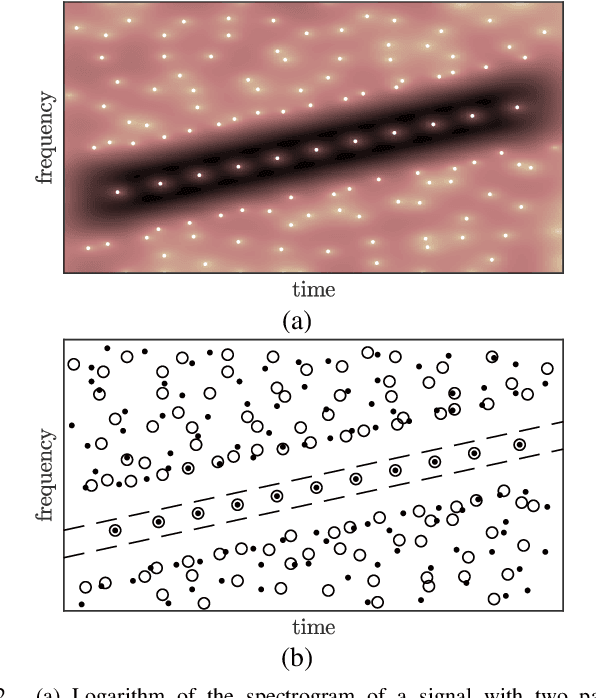
The zeros of the spectrogram have proven to be a relevant feature to describe the time-frequency structure of a signal, originated by the destructive interference between components in the time-frequency plane. In this work, a classification of these zeros in three types is introduced, based on the nature of the components that interfere to produce them. Echoing noise-assisted methods, a classification algorithm is proposed based on the addition of independent noise realizations to build a 2D histogram describing the stability of zeros. Features extracted from this histogram are later used to classify the zeros using a non-supervised clusterization algorithm. A denoising approach based on the classification of the spectrogram zeros is also introduced. Examples of the classification of zeros are given for synthetic and real signals, as well as a performance comparison of the proposed denoising algorithm with another zero-based approach.