Thomas Davies
DeepInverse: A Python package for solving imaging inverse problems with deep learning
May 26, 2025Abstract:DeepInverse is an open-source PyTorch-based library for solving imaging inverse problems. The library covers all crucial steps in image reconstruction from the efficient implementation of forward operators (e.g., optics, MRI, tomography), to the definition and resolution of variational problems and the design and training of advanced neural network architectures. In this paper, we describe the main functionality of the library and discuss the main design choices.
Canaries and Whistles: Resilient Drone Communication Networks with (or without) Deep Reinforcement Learning
Dec 08, 2023



Abstract:Communication networks able to withstand hostile environments are critically important for disaster relief operations. In this paper, we consider a challenging scenario where drones have been compromised in the supply chain, during their manufacture, and harbour malicious software capable of wide-ranging and infectious disruption. We investigate multi-agent deep reinforcement learning as a tool for learning defensive strategies that maximise communications bandwidth despite continual adversarial interference. Using a public challenge for learning network resilience strategies, we propose a state-of-the-art expert technique and study its superiority over deep reinforcement learning agents. Correspondingly, we identify three specific methods for improving the performance of our learning-based agents: (1) ensuring each observation contains the necessary information, (2) using expert agents to provide a curriculum for learning, and (3) paying close attention to reward. We apply our methods and present a new mixed strategy enabling expert and learning-based agents to work together and improve on all prior results.
* Published in AISec '23. This version fixes some terminology to improve readability
Topological Data Analysis for Anomaly Detection in Host-Based Logs
Apr 25, 2022



Abstract:Topological Data Analysis (TDA) gives practioners the ability to analyse the global structure of cybersecurity data. We use TDA for anomaly detection in host-based logs collected with the open-source Logging Made Easy (LME) project. We present an approach that builds a filtration of simplicial complexes directly from Windows logs, enabling analysis of their intrinsic structure using topological tools. We compare the efficacy of persistent homology and the spectrum of graph and hypergraph Laplacians as feature vectors against a standard log embedding that counts events, and find that topological and spectral embeddings of computer logs contain discriminative information for classifying anomalous logs that is complementary to standard embeddings. We end by discussing the potential for our methods to be used as part of an explainable framework for anomaly detection.
A Review of Topological Data Analysis for Cybersecurity
Feb 16, 2022



Abstract:In cybersecurity it is often the case that malicious or anomalous activity can only be detected by combining many weak indicators of compromise, any one of which may not raise suspicion when taken alone. The path that such indicators take can also be critical. This makes the problem of analysing cybersecurity data particularly well suited to Topological Data Analysis (TDA), a field that studies the high level structure of data using techniques from algebraic topology, both for exploratory analysis and as part of a machine learning workflow. By introducing TDA and reviewing the work done on its application to cybersecurity, we hope to highlight to researchers a promising new area with strong potential to improve cybersecurity data science.
Overfit Neural Networks as a Compact Shape Representation
Oct 12, 2020



Abstract:Neural networks have proven to be effective approximators of signed distance fields (SDFs) for solid 3D objects. While prior work has focused on the generalization power of such approximations, we instead explore their suitability as a compact - if purposefully overfit - SDF representation of individual shapes. Specifically, we ask whether neural networks can serve as first-class implicit shape representations in computer graphics. We call such overfit networks Neural Implicits. Similar to SDFs stored on a regular grid, Neural Implicits have fixed storage profiles and memory layout, but afford far greater accuracy. At equal storage cost, Neural Implicits consistently match or exceed the accuracy of irregularly-sampled triangle meshes. We achieve this with a combination of a novel loss function, sampling strategy and supervision protocol designed to facilitate robust shape overfitting. We demonstrate the flexibility of our representation on a variety of standard rendering and modelling tasks.
UV-Net: Learning from Curve-Networks and Solids
Jun 18, 2020
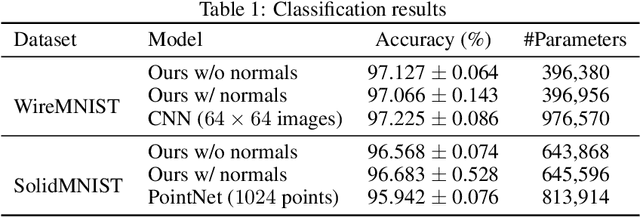

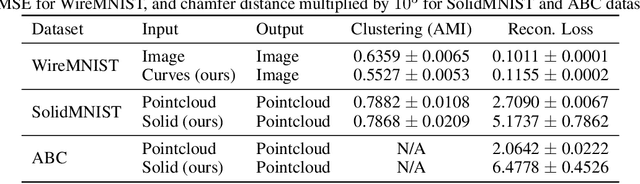
Abstract:Parametric curves, surfaces and boundary representations are the basis for 2D vector graphics and 3D industrial designs. Despite their prevalence, there exists limited research on applying modern deep neural networks directly to such representations. The unique challenges in working with such representations arise from the combination of continuous non-Euclidean geometry domain and discrete topology, as well as a lack of labeled datasets, benchmarks and baseline models. In this paper, we propose a unified representation for parametric curve-networks and solids by exploiting the u- and uv-parameter domains of curve and surfaces, respectively, to model the geometry, and an adjacency graph to explicitly model the topology. This leads to a unique and efficient network architecture based on coupled image and graph convolutional neural networks to extract features from curve-networks and solids. Inspired by the MNIST image dataset, we create and publish WireMNIST (for 2D curve-networks) and SolidMNIST (for 3D solids), two related labeled datasets depicting alphabets to encourage future research in this area. We demonstrate the effectiveness of our method using supervised and self-supervised tasks on our new datasets, as well as the publicly available ABC dataset. The results demonstrate the effectiveness of our representation and provide a competitive baseline for learning tasks involving curve-networks and solids.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge