UV-Net: Learning from Curve-Networks and Solids
Paper and Code
Jun 18, 2020
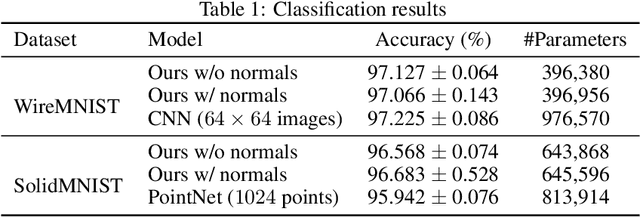

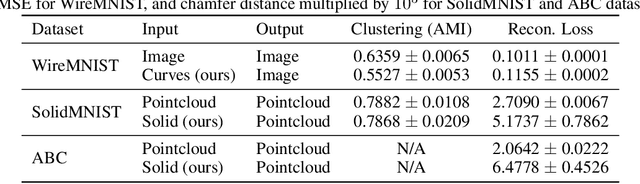
Parametric curves, surfaces and boundary representations are the basis for 2D vector graphics and 3D industrial designs. Despite their prevalence, there exists limited research on applying modern deep neural networks directly to such representations. The unique challenges in working with such representations arise from the combination of continuous non-Euclidean geometry domain and discrete topology, as well as a lack of labeled datasets, benchmarks and baseline models. In this paper, we propose a unified representation for parametric curve-networks and solids by exploiting the u- and uv-parameter domains of curve and surfaces, respectively, to model the geometry, and an adjacency graph to explicitly model the topology. This leads to a unique and efficient network architecture based on coupled image and graph convolutional neural networks to extract features from curve-networks and solids. Inspired by the MNIST image dataset, we create and publish WireMNIST (for 2D curve-networks) and SolidMNIST (for 3D solids), two related labeled datasets depicting alphabets to encourage future research in this area. We demonstrate the effectiveness of our method using supervised and self-supervised tasks on our new datasets, as well as the publicly available ABC dataset. The results demonstrate the effectiveness of our representation and provide a competitive baseline for learning tasks involving curve-networks and solids.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge