On Riemannian Stochastic Approximation Schemes with Fixed Step-Size

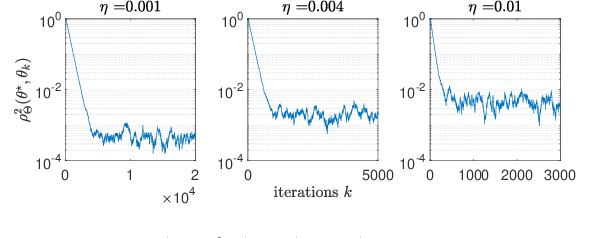
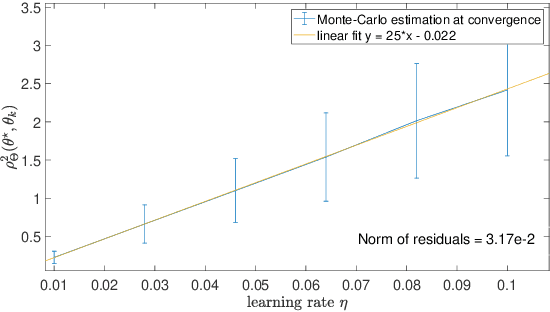
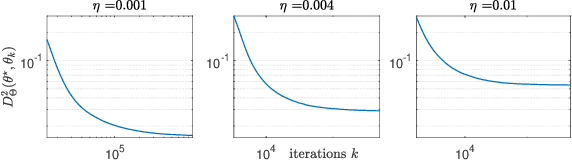
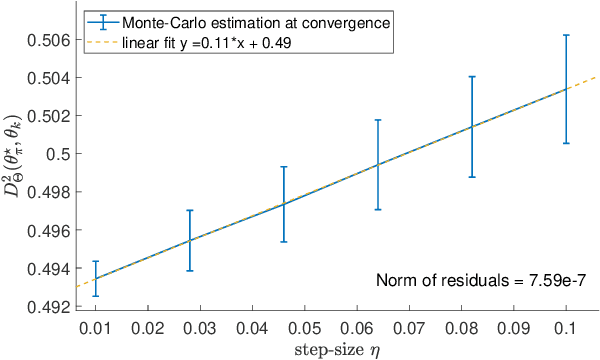
This paper studies fixed step-size stochastic approximation (SA) schemes, including stochastic gradient schemes, in a Riemannian framework. It is motivated by several applications, where geodesics can be computed explicitly, and their use accelerates crude Euclidean methods. A fixed step-size scheme defines a family of time-homogeneous Markov chains, parametrized by the step-size. Here, using this formulation, non-asymptotic performance bounds are derived, under Lyapunov conditions. Then, for any step-size, the corresponding Markov chain is proved to admit a unique stationary distribution, and to be geometrically ergodic. This result gives rise to a family of stationary distributions indexed by the step-size, which is further shown to converge to a Dirac measure, concentrated at the solution of the problem at hand, as the step-size goes to 0. Finally, the asymptotic rate of this convergence is established, through an asymptotic expansion of the bias, and a central limit theorem.

Convergence Analysis of Riemannian Stochastic Approximation Schemes

This paper analyzes the convergence for a large class of Riemannian stochastic approximation (SA) schemes, which aim at tackling stochastic optimization problems. In particular, the recursions we study use either the exponential map of the considered manifold (geodesic schemes) or more general retraction functions (retraction schemes) used as a proxy for the exponential map. Such approximations are of great interest since they are low complexity alternatives to geodesic schemes. Under the assumption that the mean field of the SA is correlated with the gradient of a smooth Lyapunov function (possibly non-convex), we show that the above Riemannian SA schemes find an ${\mathcal{O}}(b_\infty + \log n / \sqrt{n})$-stationary point (in expectation) within ${\mathcal{O}}(n)$ iterations, where $b_\infty \geq 0$ is the asymptotic bias. Compared to previous works, the conditions we derive are considerably milder. First, all our analysis are global as we do not assume iterates to be a-priori bounded. Second, we study biased SA schemes. To be more specific, we consider the case where the mean-field function can only be estimated up to a small bias, and/or the case in which the samples are drawn from a controlled Markov chain. Third, the conditions on retractions required to ensure convergence of the related SA schemes are weak and hold for well-known examples. We illustrate our results on three machine learning problems.

Human-robot Collaborative Navigation Search using Social Reward Sources

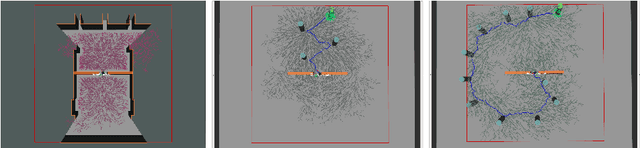
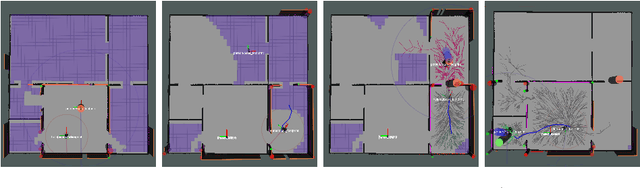
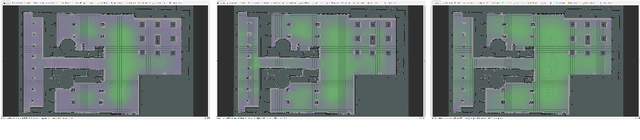
This paper proposes a Social Reward Sources (SRS) design for a Human-Robot Collaborative Navigation (HRCN) task: human-robot collaborative search. It is a flexible approach capable of handling the collaborative task, human-robot interaction and environment restrictions, all integrated on a common environment. We modelled task rewards based on unexplored area observability and isolation and evaluated the model through different levels of human-robot communication. The models are validated through quantitative evaluation against both agents' individual performance and qualitative surveying of participants' perception. After that, the three proposed communication levels are compared against each other using the previous metrics.