Geometric statistics with subspace structure preservation for SPD matrices

We present a geometric framework for the processing of SPD-valued data that preserves subspace structures and is based on the efficient computation of extreme generalized eigenvalues. This is achieved through the use of the Thompson geometry of the semidefinite cone. We explore a particular geodesic space structure in detail and establish several properties associated with it. Finally, we review a novel inductive mean of SPD matrices based on this geometry.

Differential geometry with extreme eigenvalues in the positive semidefinite cone

Differential geometric approaches to the analysis and processing of data in the form of symmetric positive definite (SPD) matrices have had notable successful applications to numerous fields including computer vision, medical imaging, and machine learning. The dominant geometric paradigm for such applications has consisted of a few Riemannian geometries associated with spectral computations that are costly at high scale and in high dimensions. We present a route to a scalable geometric framework for the analysis and processing of SPD-valued data based on the efficient computation of extreme generalized eigenvalues through the Hilbert and Thompson geometries of the semidefinite cone. We explore a particular geodesic space structure based on Thompson geometry in detail and establish several properties associated with this structure. Furthermore, we define a novel iterative mean of SPD matrices based on this geometry and prove its existence and uniqueness for a given finite collection of points. Finally, we state and prove a number of desirable properties that are satisfied by this mean.

Estimating long-term causal effects from short-term experiments and long-term observational data with unobserved confounding

Understanding and quantifying cause and effect is an important problem in many domains. The generally-agreed solution to this problem is to perform a randomised controlled trial. However, even when randomised controlled trials can be performed, they usually have relatively short duration's due to cost considerations. This makes learning long-term causal effects a very challenging task in practice, since the long-term outcome is only observed after a long delay. In this paper, we study the identification and estimation of long-term treatment effects when both experimental and observational data are available. Previous work provided an estimation strategy to determine long-term causal effects from such data regimes. However, this strategy only works if one assumes there are no unobserved confounders in the observational data. In this paper, we specifically address the challenging case where unmeasured confounders are present in the observational data. Our long-term causal effect estimator is obtained by combining regression residuals with short-term experimental outcomes in a specific manner to create an instrumental variable, which is then used to quantify the long-term causal effect through instrumental variable regression. We prove this estimator is unbiased, and analytically study its variance. In the context of the front-door causal structure, this provides a new causal estimator, which may be of independent interest. Finally, we empirically test our approach on synthetic-data, as well as real-data from the International Stroke Trial.

Fast Regression of the Tritium Breeding Ratio in Fusion Reactors

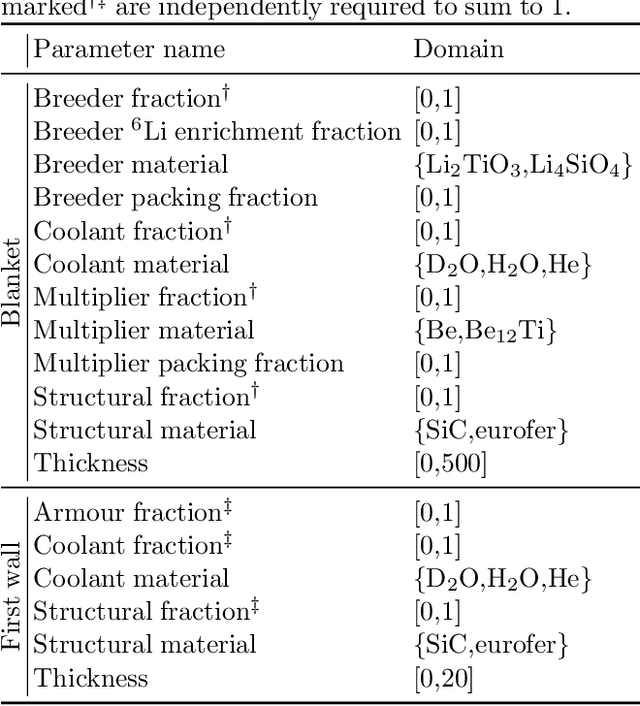
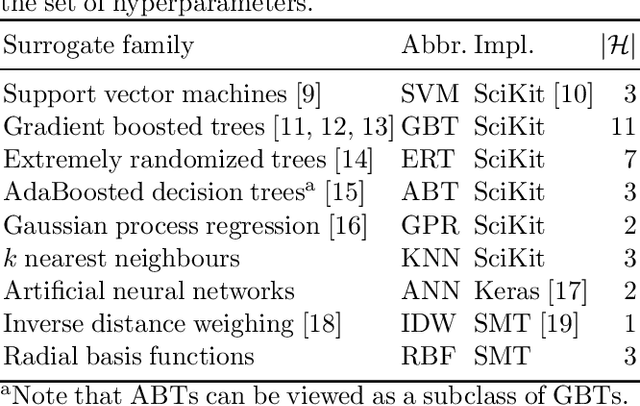
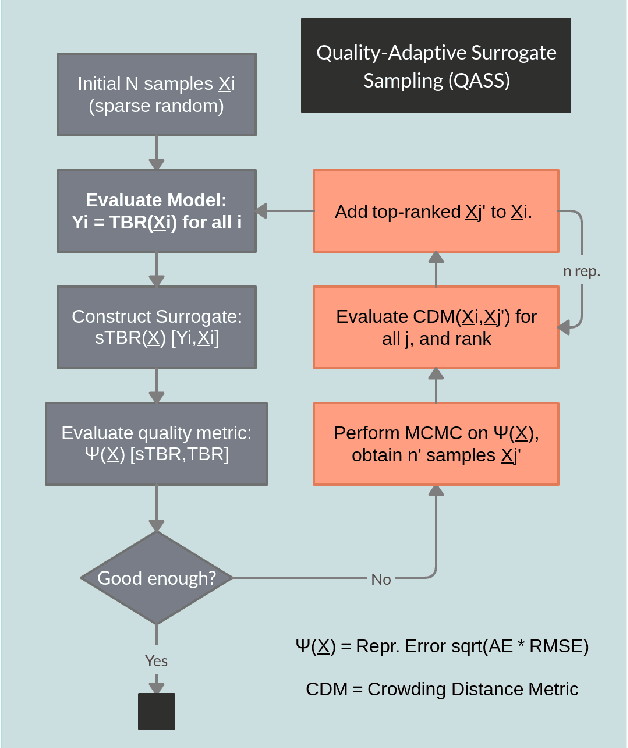
The tritium breeding ratio (TBR) is an essential quantity for the design of modern and next-generation D-T fueled nuclear fusion reactors. Representing the ratio between tritium fuel generated in breeding blankets and fuel consumed during reactor runtime, the TBR depends on reactor geometry and material properties in a complex manner. In this work, we explored the training of surrogate models to produce a cheap but high-quality approximation for a Monte Carlo TBR model in use at the UK Atomic Energy Authority. We investigated possibilities for dimensional reduction of its feature space, reviewed 9 families of surrogate models for potential applicability, and performed hyperparameter optimisation. Here we present the performance and scaling properties of these models, the fastest of which, an artificial neural network, demonstrated $R^2=0.985$ and a mean prediction time of $0.898\ \mu\mathrm{s}$, representing a relative speedup of $8\cdot 10^6$ with respect to the expensive MC model. We further present a novel adaptive sampling algorithm, Quality-Adaptive Surrogate Sampling, capable of interfacing with any of the individually studied surrogates. Our preliminary testing on a toy TBR theory has demonstrated the efficacy of this algorithm for accelerating the surrogate modelling process.