Kinematic control design for wheeled mobile robots with longitudinal and lateral slip

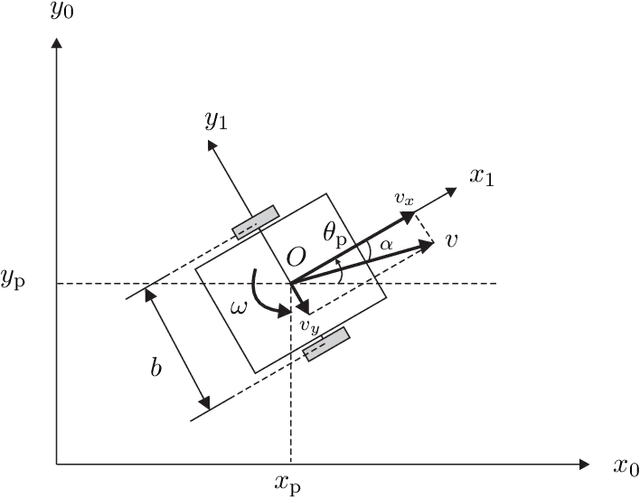
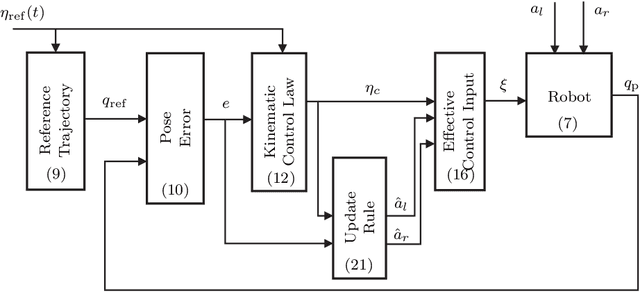
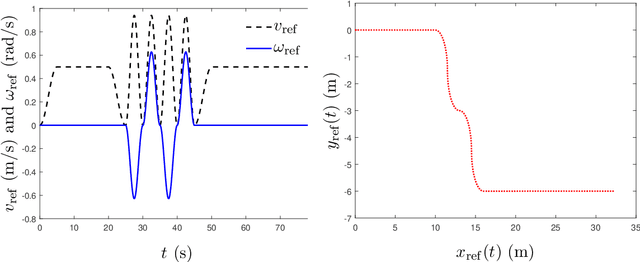
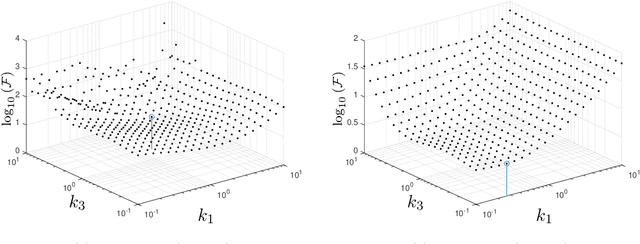
The motion control of wheeled mobile robots at high speeds under adverse ground conditions is a difficult task, since the robots' wheels may be subject to different kinds of slip. This work introduces an adaptive kinematic controller that is capable of solving the trajectory tracking problem of a nonholonomic mobile robot under longitudinal and lateral slip. While the controller can effectively compensate for the longitudinal slip, the lateral slip is a more involved problem to deal with, since nonholonomic robots cannot directly produce movement in the lateral direction. To show that the proposed controller is still able to make the mobile robot follow a reference trajectory under lateral and longitudinal time-varying slip, the solutions of the robot's position and orientation error dynamics are shown to be uniformly ultimately bounded. Numerical simulations are presented to illustrate the robot's performance using the proposed adaptive control law.

System identification of biophysical neuronal models

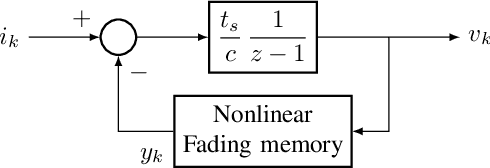
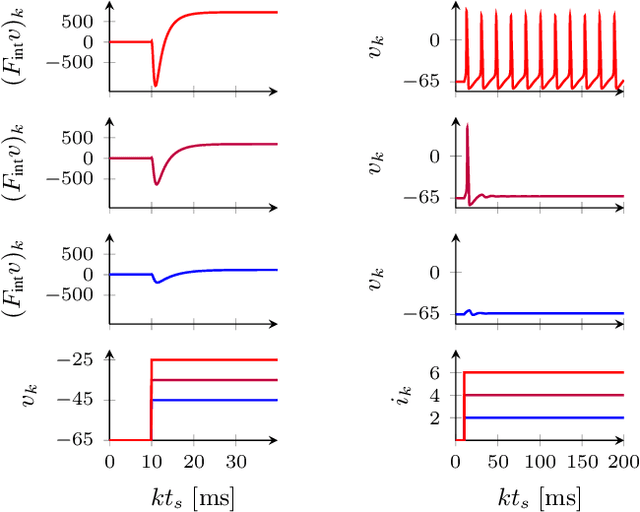
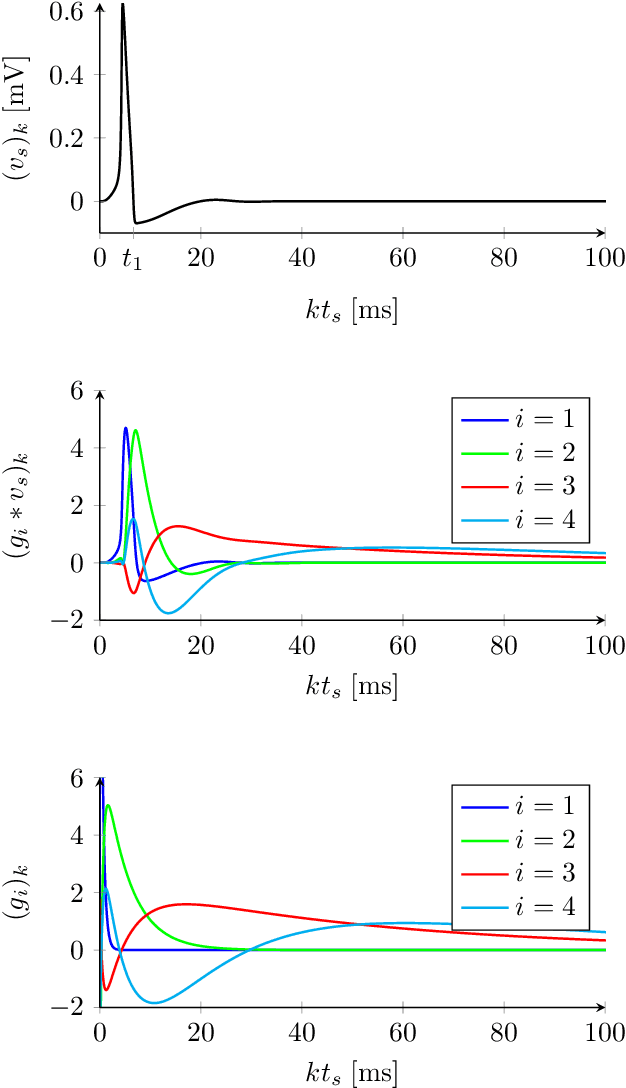
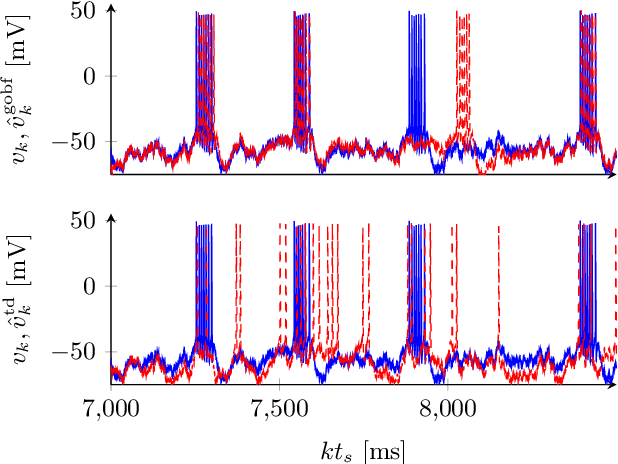
After sixty years of quantitative biophysical modeling of neurons, the identification of neuronal dynamics from input-output data remains a challenging problem, primarily due to the inherently nonlinear nature of excitable behaviors. By reformulating the problem in terms of the identification of an operator with fading memory, we explore a simple approach based on a parametrization given by a series interconnection of Generalized Orthonormal Basis Functions (GOBFs) and static Artificial Neural Networks. We show that GOBFs are particularly well-suited to tackle the identification problem, and provide a heuristic for selecting GOBF poles which addresses the ultra-sensitivity of neuronal behaviors. The method is illustrated on the identification of a bursting model from the crab stomatogastric ganglion.