Juncal Arbelaiz
Excitable crawling
May 31, 2024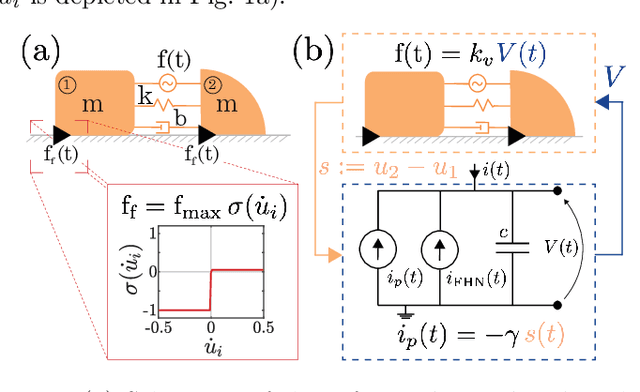
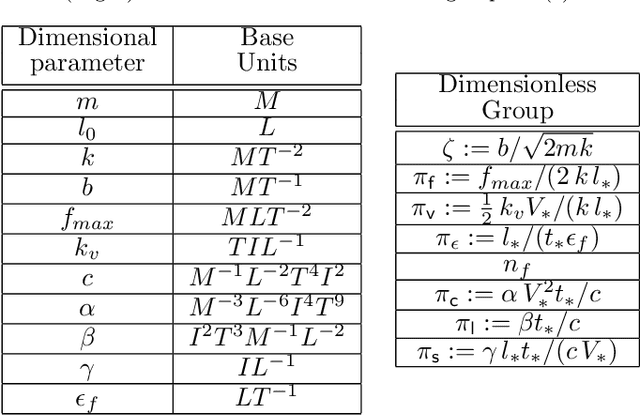
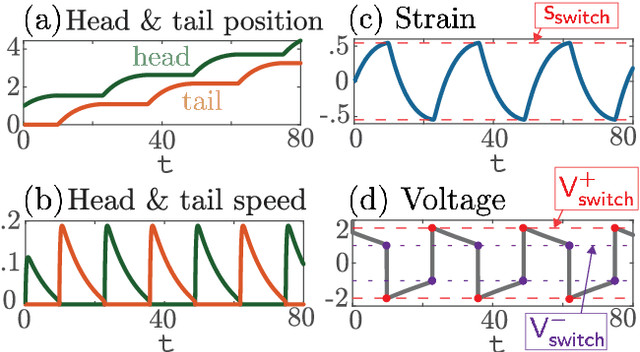
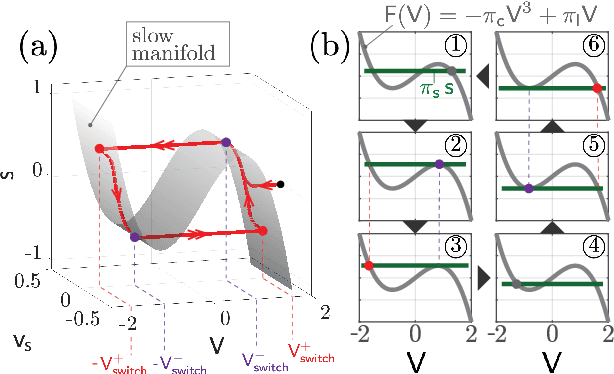
Abstract:We propose and analyze the suitability of a spiking controller to engineer the locomotion of a soft robotic crawler. Inspired by the FitzHugh-Nagumo model of neural excitability, we design a bistable controller with an electrical flipflop circuit representation capable of generating spikes on-demand when coupled to the passive crawler mechanics. A proprioceptive sensory signal from the crawler mechanics turns bistability of the controller into a rhythmic spiking. The output voltage, in turn, activates the crawler's actuators to generate movement through peristaltic waves. We show through geometric analysis that this control strategy achieves endogenous crawling. The electro-mechanical sensorimotor interconnection provides embodied negative feedback regulation, facilitating locomotion. Dimensional analysis provides insights on the characteristic scales in the crawler's mechanical and electrical dynamics, and how they determine the crawling gait. Adaptive control of the electrical scales to optimally match the mechanical scales can be envisioned to achieve further efficiency, as in homeostatic regulation of neuronal circuits. Our approach can scale up to multiple sensorimotor loops inspired by biological central pattern generators.
Personalized Cancer Chemotherapy Schedule: a numerical comparison of performance and robustness in model-based and model-free scheduling methodologies
Apr 06, 2019
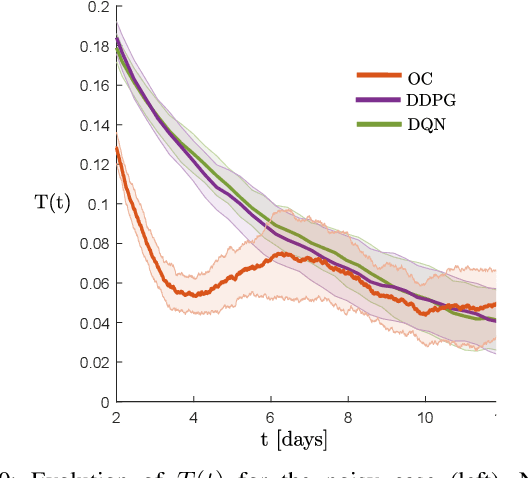
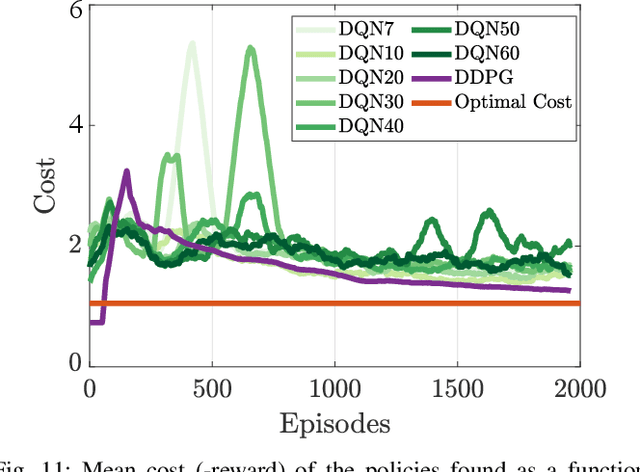
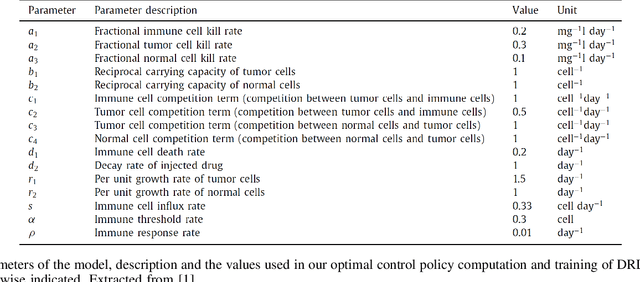
Abstract:Reinforcement learning algorithms are gaining popularity in fields where optimal scheduling is important, and oncology is not an exception. The complex and uncertain dynamics of cancer limit the performance of traditional model-based scheduling strategies like Optimal Control. Motivated by the recent success of model-free Deep Reinforcement Learning (DRL) in challenging control tasks and in medical treatments, we use Deep Q-Network (DQN) and Deep Deterministic Policy Gradient (DDPG) to design a personalized cancer chemotherapy schedule. We show that both of them succeed in the task and outperform the Optimal Control solution in the presence of uncertainty. Furthermore, we show that DDPG can exterminate cancer more efficiently than DQN due to its continuous action space. Finally, we provide some intuition regarding the amount of samples required for the training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge