Modeling and Estimation of Discrete-Time Reciprocal Processes via Probabilistic Graphical Models

Reciprocal processes are acausal generalizations of Markov processes introduced by Bernstein in 1932. In the literature, a significant amount of attention has been focused on developing dynamical models for reciprocal processes. In this paper, we provide a probabilistic graphical model for reciprocal processes. This leads to a principled solution of the smoothing problem via message passing algorithms. For the finite state space case, convergence analysis is revisited via the Hilbert metric.

On the Geometry of Message Passing Algorithms for Gaussian Reciprocal Processes

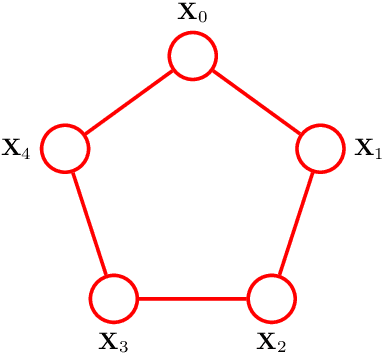
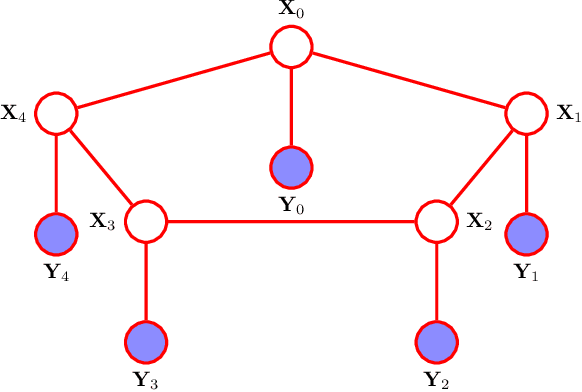
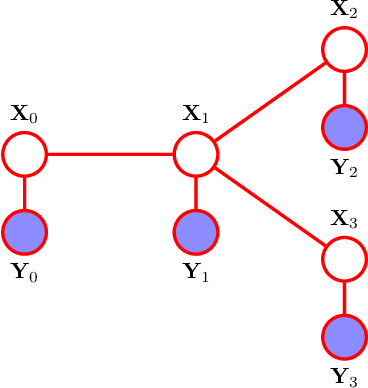
Reciprocal processes are acausal generalizations of Markov processes introduced by Bernstein in 1932. In the literature, a significant amount of attention has been focused on developing dynamical models for reciprocal processes. Recently, probabilistic graphical models for reciprocal processes have been provided. This opens the way to the application of efficient inference algorithms in the machine learning literature to solve the smoothing problem for reciprocal processes. Such algorithms are known to converge if the underlying graph is a tree. This is not the case for a reciprocal process, whose associated graphical model is a single loop network. The contribution of this paper is twofold. First, we introduce belief propagation for Gaussian reciprocal processes. Second, we establish a link between convergence analysis of belief propagation for Gaussian reciprocal processes and stability theory for differentially positive systems.

Maximum Entropy Kernels for System Identification

A new nonparametric approach for system identification has been recently proposed where the impulse response is modeled as the realization of a zero-mean Gaussian process whose covariance (kernel) has to be estimated from data. In this scheme, quality of the estimates crucially depends on the parametrization of the covariance of the Gaussian process. A family of kernels that have been shown to be particularly effective in the system identification framework is the family of Diagonal/Correlated (DC) kernels. Maximum entropy properties of a related family of kernels, the Tuned/Correlated (TC) kernels, have been recently pointed out in the literature. In this paper we show that maximum entropy properties indeed extend to the whole family of DC kernels. The maximum entropy interpretation can be exploited in conjunction with results on matrix completion problems in the graphical models literature to shed light on the structure of the DC kernel. In particular, we prove that the DC kernel admits a closed-form factorization, inverse and determinant. These results can be exploited both to improve the numerical stability and to reduce the computational complexity associated with the computation of the DC estimator.

On the Projective Geometry of Kalman Filter

Convergence of the Kalman filter is best analyzed by studying the contraction of the Riccati map in the space of positive definite (covariance) matrices. In this paper, we explore how this contraction property relates to a more fundamental non-expansiveness property of filtering maps in the space of probability distributions endowed with the Hilbert metric. This is viewed as a preliminary step towards improving the convergence analysis of filtering algorithms over general graphical models.

On the Maximum Entropy Property of the First-Order Stable Spline Kernel and its Implications

A new nonparametric approach for system identification has been recently proposed where the impulse response is seen as the realization of a zero--mean Gaussian process whose covariance, the so--called stable spline kernel, guarantees that the impulse response is almost surely stable. Maximum entropy properties of the stable spline kernel have been pointed out in the literature. In this paper we provide an independent proof that relies on the theory of matrix extension problems in the graphical model literature and leads to a closed form expression for the inverse of the first order stable spline kernel as well as to a new factorization in the form $UWU^\top$ with $U$ upper triangular and $W$ diagonal. Interestingly, all first--order stable spline kernels share the same factor $U$ and $W$ admits a closed form representation in terms of the kernel hyperparameter, making the factorization computationally inexpensive. Maximum likelihood properties of the stable spline kernel are also highlighted. These results can be applied both to improve the stability and to reduce the computational complexity associated with the computation of stable spline estimators.