Deep Learning of Dynamic Systems using System Identification Toolbox(TM)

MATLAB(R) releases over the last 3 years have witnessed a continuing growth in the dynamic modeling capabilities offered by the System Identification Toolbox(TM). The emphasis has been on integrating deep learning architectures and training techniques that facilitate the use of deep neural networks as building blocks of nonlinear models. The toolbox offers neural state-space models which can be extended with auto-encoding features that are particularly suited for reduced-order modeling of large systems. The toolbox contains several other enhancements that deepen its integration with the state-of-art machine learning techniques, leverage auto-differentiation features for state estimation, and enable a direct use of raw numeric matrices and timetables for training models.

Deep networks for system identification: a Survey

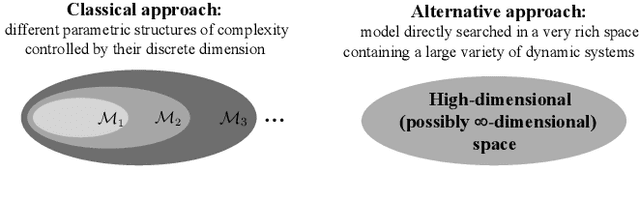
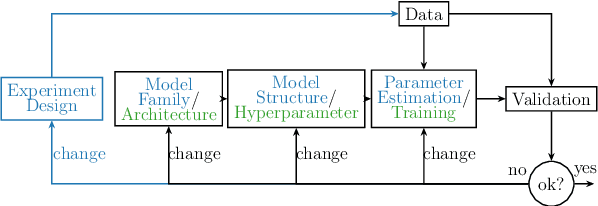
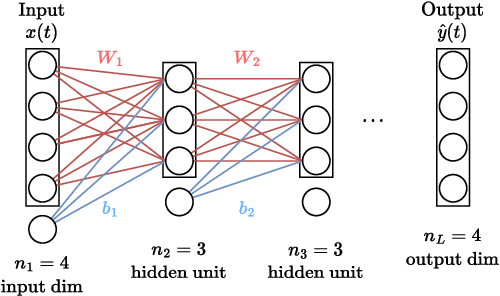
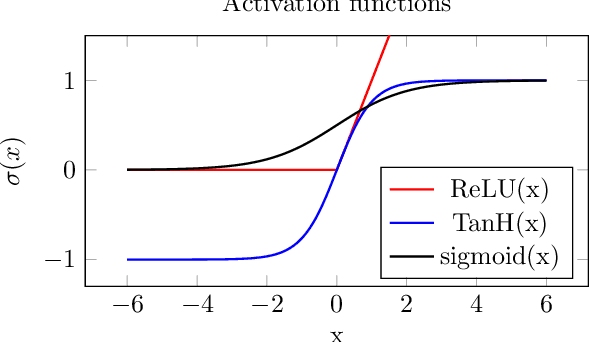
Deep learning is a topic of considerable current interest. The availability of massive data collections and powerful software resources has led to an impressive amount of results in many application areas that reveal essential but hidden properties of the observations. System identification learns mathematical descriptions of dynamic systems from input-output data and can thus benefit from the advances of deep neural networks to enrich the possible range of models to choose from. For this reason, we provide a survey of deep learning from a system identification perspective. We cover a wide spectrum of topics to enable researchers to understand the methods, providing rigorous practical and theoretical insights into the benefits and challenges of using them. The main aim of the identified model is to predict new data from previous observations. This can be achieved with different deep learning based modelling techniques and we discuss architectures commonly adopted in the literature, like feedforward, convolutional, and recurrent networks. Their parameters have to be estimated from past data trying to optimize the prediction performance. For this purpose, we discuss a specific set of first-order optimization tools that is emerged as efficient. The survey then draws connections to the well-studied area of kernel-based methods. They control the data fit by regularization terms that penalize models not in line with prior assumptions. We illustrate how to cast them in deep architectures to obtain deep kernel-based methods. The success of deep learning also resulted in surprising empirical observations, like the counter-intuitive behaviour of models with many parameters. We discuss the role of overparameterized models, including their connection to kernels, as well as implicit regularization mechanisms which affect generalization, specifically the interesting phenomena of benign overfitting ...

A Crash Course on Reinforcement Learning

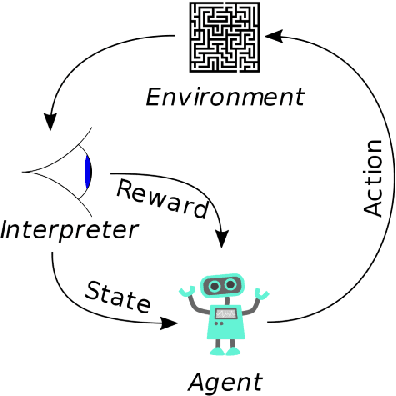
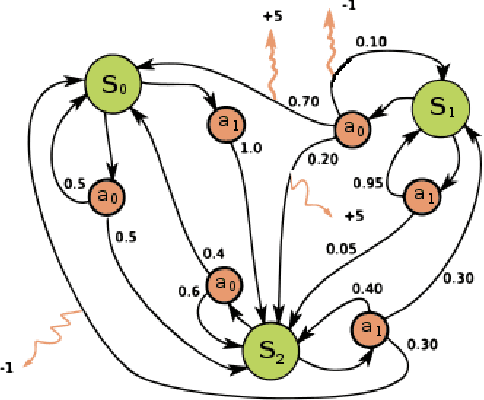
The emerging field of Reinforcement Learning (RL) has led to impressive results in varied domains like strategy games, robotics, etc. This handout aims to give a simple introduction to RL from control perspective and discuss three possible approaches to solve an RL problem: Policy Gradient, Policy Iteration, and Model-building. Dynamical systems might have discrete action-space like cartpole where two possible actions are +1 and -1 or continuous action space like linear Gaussian systems. Our discussion covers both cases.

Deep State Space Models for Nonlinear System Identification

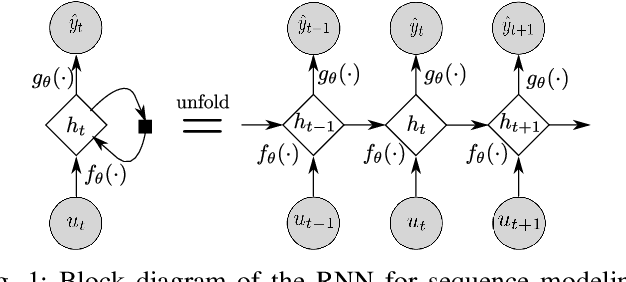
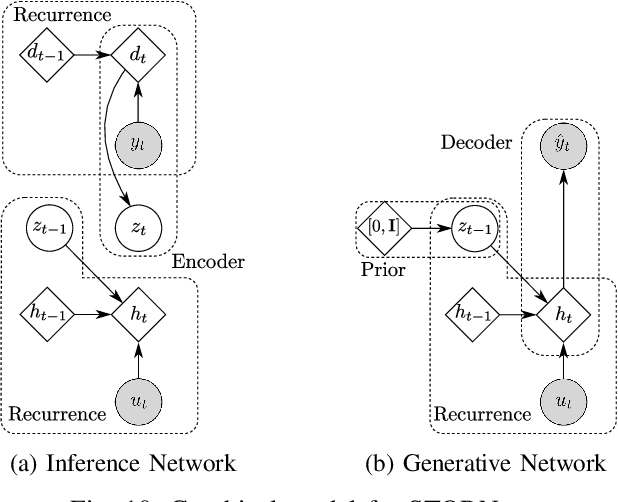
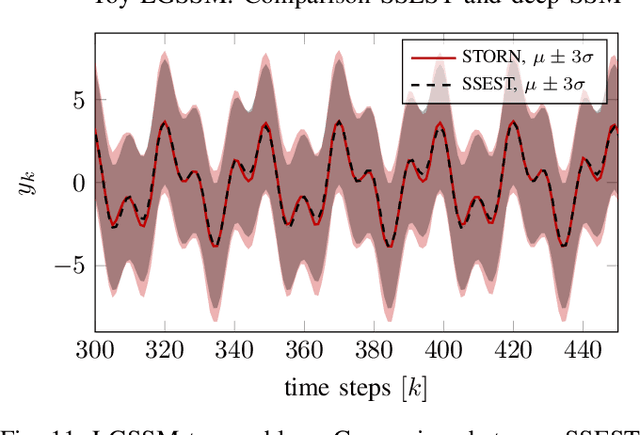
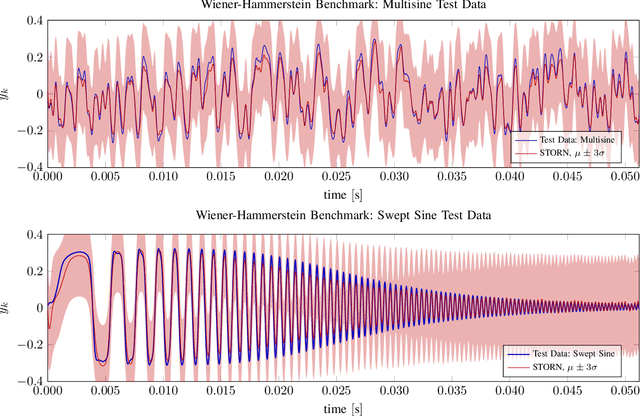
An actively evolving model class for generative temporal models developed in the deep learning community are deep state space models (SSMs) which have a close connection to classic SSMs. In this work six new deep SSMs are implemented and evaluated for the identification of established nonlinear dynamic system benchmarks. The models and their parameter learning algorithms are elaborated rigorously. The usage of deep SSMs as a black-box identification model can describe a wide range of dynamics due to the flexibility of deep neural networks. Additionally, the uncertainty of the system is modelled and therefore one obtains a much richer representation and a whole class of systems to describe the underlying dynamics.

Maximum Entropy Kernels for System Identification

A new nonparametric approach for system identification has been recently proposed where the impulse response is modeled as the realization of a zero-mean Gaussian process whose covariance (kernel) has to be estimated from data. In this scheme, quality of the estimates crucially depends on the parametrization of the covariance of the Gaussian process. A family of kernels that have been shown to be particularly effective in the system identification framework is the family of Diagonal/Correlated (DC) kernels. Maximum entropy properties of a related family of kernels, the Tuned/Correlated (TC) kernels, have been recently pointed out in the literature. In this paper we show that maximum entropy properties indeed extend to the whole family of DC kernels. The maximum entropy interpretation can be exploited in conjunction with results on matrix completion problems in the graphical models literature to shed light on the structure of the DC kernel. In particular, we prove that the DC kernel admits a closed-form factorization, inverse and determinant. These results can be exploited both to improve the numerical stability and to reduce the computational complexity associated with the computation of the DC estimator.

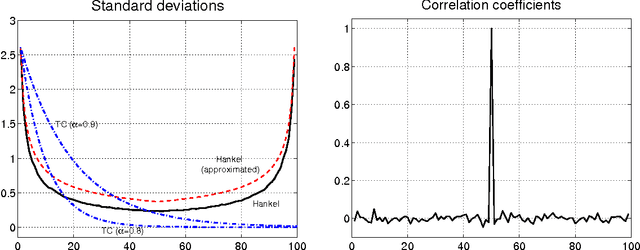
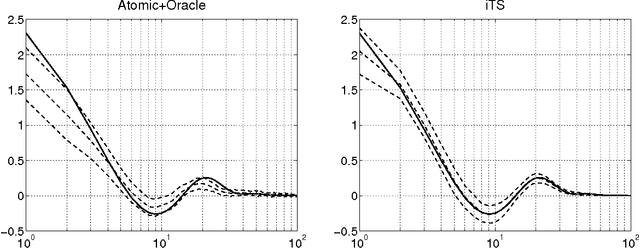
Regularized linear system identification using atomic, nuclear and kernel-based norms: the role of the stability constraint

Inspired by ideas taken from the machine learning literature, new regularization techniques have been recently introduced in linear system identification. In particular, all the adopted estimators solve a regularized least squares problem, differing in the nature of the penalty term assigned to the impulse response. Popular choices include atomic and nuclear norms (applied to Hankel matrices) as well as norms induced by the so called stable spline kernels. In this paper, a comparative study of estimators based on these different types of regularizers is reported. Our findings reveal that stable spline kernels outperform approaches based on atomic and nuclear norms since they suitably embed information on impulse response stability and smoothness. This point is illustrated using the Bayesian interpretation of regularization. We also design a new class of regularizers defined by "integral" versions of stable spline/TC kernels. Under quite realistic experimental conditions, the new estimators outperform classical prediction error methods also when the latter are equipped with an oracle for model order selection.

Scalable Anomaly Detection in Large Homogenous Populations

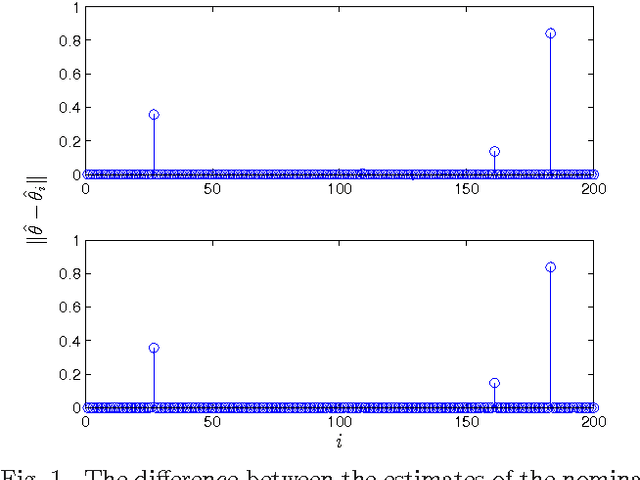
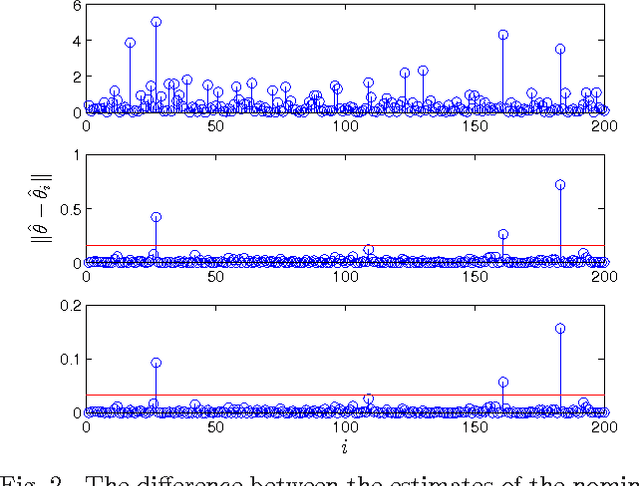
Anomaly detection in large populations is a challenging but highly relevant problem. The problem is essentially a multi-hypothesis problem, with a hypothesis for every division of the systems into normal and anomal systems. The number of hypothesis grows rapidly with the number of systems and approximate solutions become a necessity for any problems of practical interests. In the current paper we take an optimization approach to this multi-hypothesis problem. We first observe that the problem is equivalent to a non-convex combinatorial optimization problem. We then relax the problem to a convex problem that can be solved distributively on the systems and that stays computationally tractable as the number of systems increase. An interesting property of the proposed method is that it can under certain conditions be shown to give exactly the same result as the combinatorial multi-hypothesis problem and the relaxation is hence tight.