Detection of Chagas Disease from the ECG: The George B. Moody PhysioNet Challenge 2025

Objective: Chagas disease is a parasitic infection that is endemic to South America, Central America, and, more recently, the U.S., primarily transmitted by insects. Chronic Chagas disease can cause cardiovascular diseases and digestive problems. Serological testing capacities for Chagas disease are limited, but Chagas cardiomyopathy often manifests in ECGs, providing an opportunity to prioritize patients for testing and treatment. Approach: The George B. Moody PhysioNet Challenge 2025 invites teams to develop algorithmic approaches for identifying Chagas disease from electrocardiograms (ECGs). Main results: This Challenge provides multiple innovations. First, we leveraged several datasets with labels from patient reports and serological testing, provided a large dataset with weak labels and smaller datasets with strong labels. Second, we augmented the data to support model robustness and generalizability to unseen data sources. Third, we applied an evaluation metric that captured the local serological testing capacity for Chagas disease to frame the machine learning problem as a triage task. Significance: Over 630 participants from 111 teams submitted over 1300 entries during the Challenge, representing diverse approaches from academia and industry worldwide.

Explaining deep learning for ECG using time-localized clusters

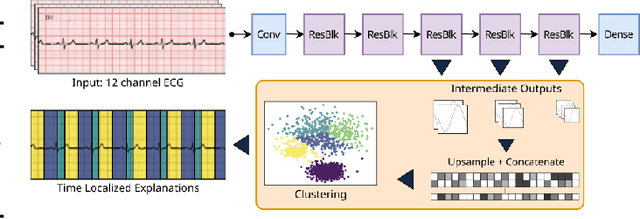
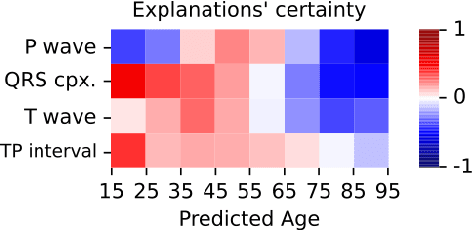
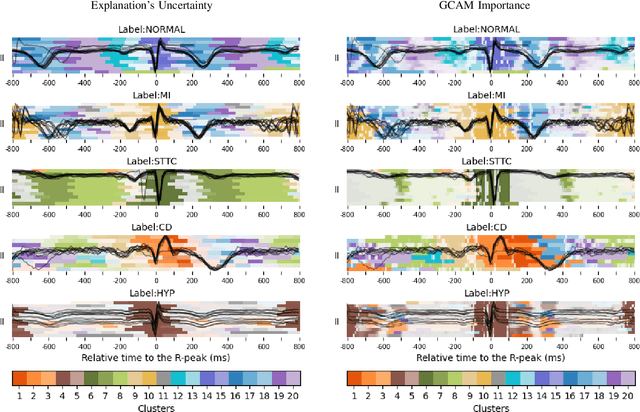
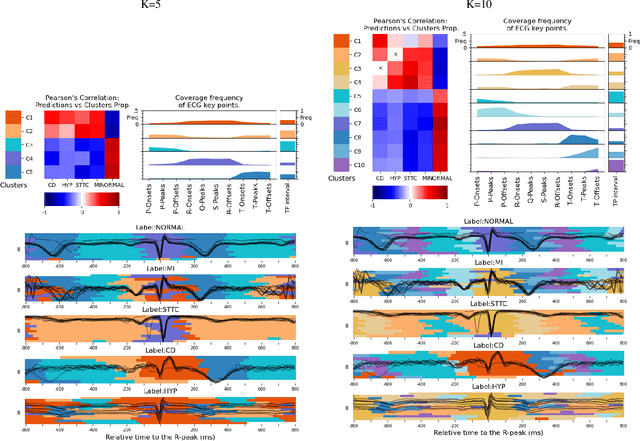
Deep learning has significantly advanced electrocardiogram (ECG) analysis, enabling automatic annotation, disease screening, and prognosis beyond traditional clinical capabilities. However, understanding these models remains a challenge, limiting interpretation and gaining knowledge from these developments. In this work, we propose a novel interpretability method for convolutional neural networks applied to ECG analysis. Our approach extracts time-localized clusters from the model's internal representations, segmenting the ECG according to the learned characteristics while quantifying the uncertainty of these representations. This allows us to visualize how different waveform regions contribute to the model's predictions and assess the certainty of its decisions. By providing a structured and interpretable view of deep learning models for ECG, our method enhances trust in AI-driven diagnostics and facilitates the discovery of clinically relevant electrophysiological patterns.

On the Interaction of Compressibility and Adversarial Robustness

Modern neural networks are expected to simultaneously satisfy a host of desirable properties: accurate fitting to training data, generalization to unseen inputs, parameter and computational efficiency, and robustness to adversarial perturbations. While compressibility and robustness have each been studied extensively, a unified understanding of their interaction still remains elusive. In this work, we develop a principled framework to analyze how different forms of compressibility - such as neuron-level sparsity and spectral compressibility - affect adversarial robustness. We show that these forms of compression can induce a small number of highly sensitive directions in the representation space, which adversaries can exploit to construct effective perturbations. Our analysis yields a simple yet instructive robustness bound, revealing how neuron and spectral compressibility impact $L_\infty$ and $L_2$ robustness via their effects on the learned representations. Crucially, the vulnerabilities we identify arise irrespective of how compression is achieved - whether via regularization, architectural bias, or implicit learning dynamics. Through empirical evaluations across synthetic and realistic tasks, we confirm our theoretical predictions, and further demonstrate that these vulnerabilities persist under adversarial training and transfer learning, and contribute to the emergence of universal adversarial perturbations. Our findings show a fundamental tension between structured compressibility and robustness, and suggest new pathways for designing models that are both efficient and secure.

Human-Aligned Image Models Improve Visual Decoding from the Brain

Decoding visual images from brain activity has significant potential for advancing brain-computer interaction and enhancing the understanding of human perception. Recent approaches align the representation spaces of images and brain activity to enable visual decoding. In this paper, we introduce the use of human-aligned image encoders to map brain signals to images. We hypothesize that these models more effectively capture perceptual attributes associated with the rapid visual stimuli presentations commonly used in visual brain data recording experiments. Our empirical results support this hypothesis, demonstrating that this simple modification improves image retrieval accuracy by up to 21% compared to state-of-the-art methods. Comprehensive experiments confirm consistent performance improvements across diverse EEG architectures, image encoders, alignment methods, participants, and brain imaging modalities.

Can Transformers Smell Like Humans?

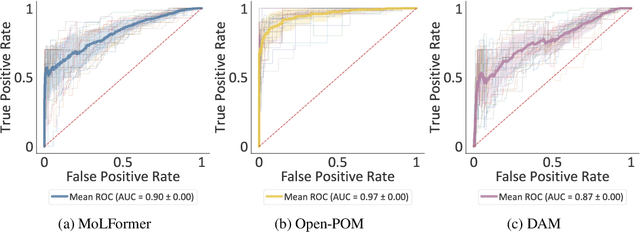
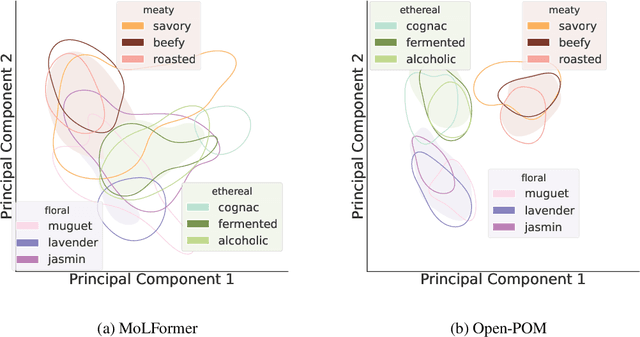
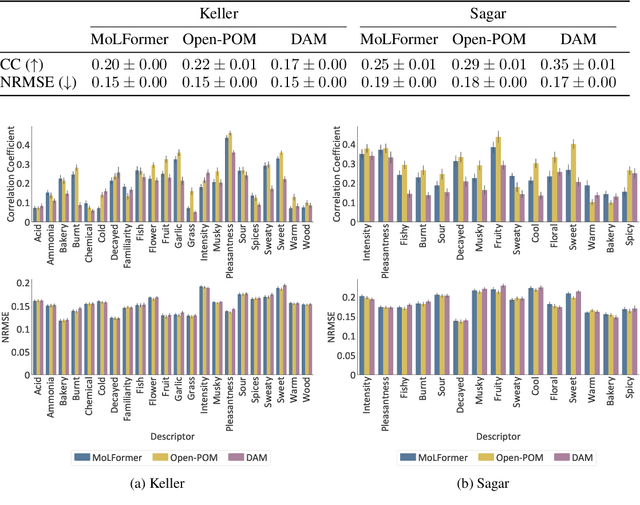
The human brain encodes stimuli from the environment into representations that form a sensory perception of the world. Despite recent advances in understanding visual and auditory perception, olfactory perception remains an under-explored topic in the machine learning community due to the lack of large-scale datasets annotated with labels of human olfactory perception. In this work, we ask the question of whether pre-trained transformer models of chemical structures encode representations that are aligned with human olfactory perception, i.e., can transformers smell like humans? We demonstrate that representations encoded from transformers pre-trained on general chemical structures are highly aligned with human olfactory perception. We use multiple datasets and different types of perceptual representations to show that the representations encoded by transformer models are able to predict: (i) labels associated with odorants provided by experts; (ii) continuous ratings provided by human participants with respect to pre-defined descriptors; and (iii) similarity ratings between odorants provided by human participants. Finally, we evaluate the extent to which this alignment is associated with physicochemical features of odorants known to be relevant for olfactory decoding.

Regularization properties of adversarially-trained linear regression

State-of-the-art machine learning models can be vulnerable to very small input perturbations that are adversarially constructed. Adversarial training is an effective approach to defend against it. Formulated as a min-max problem, it searches for the best solution when the training data were corrupted by the worst-case attacks. Linear models are among the simple models where vulnerabilities can be observed and are the focus of our study. In this case, adversarial training leads to a convex optimization problem which can be formulated as the minimization of a finite sum. We provide a comparative analysis between the solution of adversarial training in linear regression and other regularization methods. Our main findings are that: (A) Adversarial training yields the minimum-norm interpolating solution in the overparameterized regime (more parameters than data), as long as the maximum disturbance radius is smaller than a threshold. And, conversely, the minimum-norm interpolator is the solution to adversarial training with a given radius. (B) Adversarial training can be equivalent to parameter shrinking methods (ridge regression and Lasso). This happens in the underparametrized region, for an appropriate choice of adversarial radius and zero-mean symmetrically distributed covariates. (C) For $\ell_\infty$-adversarial training -- as in square-root Lasso -- the choice of adversarial radius for optimal bounds does not depend on the additive noise variance. We confirm our theoretical findings with numerical examples.

End-to-end Risk Prediction of Atrial Fibrillation from the 12-Lead ECG by Deep Neural Networks

Background: Atrial fibrillation (AF) is one of the most common cardiac arrhythmias that affects millions of people each year worldwide and it is closely linked to increased risk of cardiovascular diseases such as stroke and heart failure. Machine learning methods have shown promising results in evaluating the risk of developing atrial fibrillation from the electrocardiogram. We aim to develop and evaluate one such algorithm on a large CODE dataset collected in Brazil. Results: The deep neural network model identified patients without indication of AF in the presented ECG but who will develop AF in the future with an AUC score of 0.845. From our survival model, we obtain that patients in the high-risk group (i.e. with the probability of a future AF case being greater than 0.7) are 50% more likely to develop AF within 40 weeks, while patients belonging to the minimal-risk group (i.e. with the probability of a future AF case being less than or equal to 0.1) have more than 85% chance of remaining AF free up until after seven years. Conclusion: We developed and validated a model for AF risk prediction. If applied in clinical practice, the model possesses the potential of providing valuable and useful information in decision-making and patient management processes.

Deep networks for system identification: a Survey

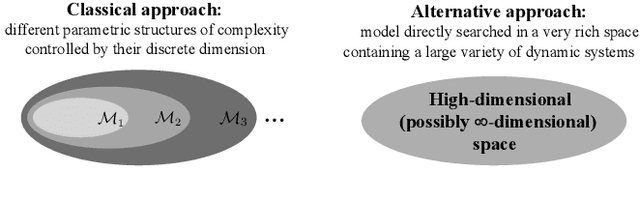
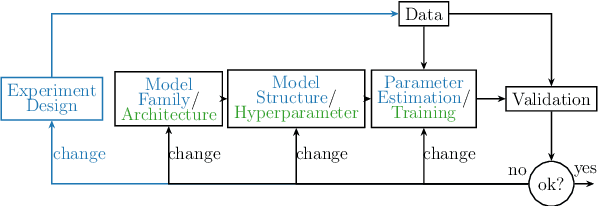
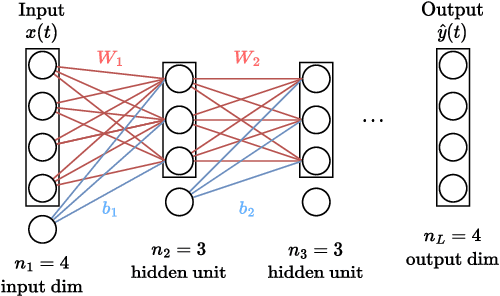
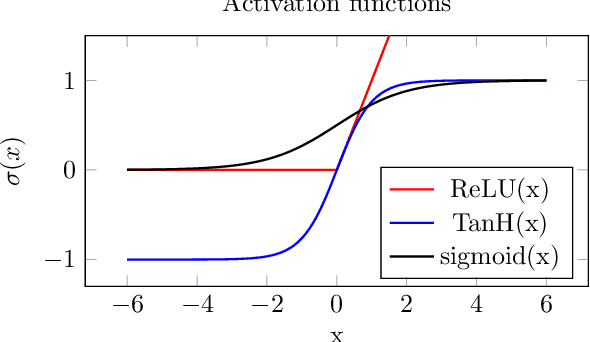
Deep learning is a topic of considerable current interest. The availability of massive data collections and powerful software resources has led to an impressive amount of results in many application areas that reveal essential but hidden properties of the observations. System identification learns mathematical descriptions of dynamic systems from input-output data and can thus benefit from the advances of deep neural networks to enrich the possible range of models to choose from. For this reason, we provide a survey of deep learning from a system identification perspective. We cover a wide spectrum of topics to enable researchers to understand the methods, providing rigorous practical and theoretical insights into the benefits and challenges of using them. The main aim of the identified model is to predict new data from previous observations. This can be achieved with different deep learning based modelling techniques and we discuss architectures commonly adopted in the literature, like feedforward, convolutional, and recurrent networks. Their parameters have to be estimated from past data trying to optimize the prediction performance. For this purpose, we discuss a specific set of first-order optimization tools that is emerged as efficient. The survey then draws connections to the well-studied area of kernel-based methods. They control the data fit by regularization terms that penalize models not in line with prior assumptions. We illustrate how to cast them in deep architectures to obtain deep kernel-based methods. The success of deep learning also resulted in surprising empirical observations, like the counter-intuitive behaviour of models with many parameters. We discuss the role of overparameterized models, including their connection to kernels, as well as implicit regularization mechanisms which affect generalization, specifically the interesting phenomena of benign overfitting ...

ECG-Based Electrolyte Prediction: Evaluating Regression and Probabilistic Methods

Objective: Imbalances of the electrolyte concentration levels in the body can lead to catastrophic consequences, but accurate and accessible measurements could improve patient outcomes. While blood tests provide accurate measurements, they are invasive and the laboratory analysis can be slow or inaccessible. In contrast, an electrocardiogram (ECG) is a widely adopted tool which is quick and simple to acquire. However, the problem of estimating continuous electrolyte concentrations directly from ECGs is not well-studied. We therefore investigate if regression methods can be used for accurate ECG-based prediction of electrolyte concentrations. Methods: We explore the use of deep neural networks (DNNs) for this task. We analyze the regression performance across four electrolytes, utilizing a novel dataset containing over 290000 ECGs. For improved understanding, we also study the full spectrum from continuous predictions to binary classification of extreme concentration levels. To enhance clinical usefulness, we finally extend to a probabilistic regression approach and evaluate different uncertainty estimates. Results: We find that the performance varies significantly between different electrolytes, which is clinically justified in the interplay of electrolytes and their manifestation in the ECG. We also compare the regression accuracy with that of traditional machine learning models, demonstrating superior performance of DNNs. Conclusion: Discretization can lead to good classification performance, but does not help solve the original problem of predicting continuous concentration levels. While probabilistic regression demonstrates potential practical usefulness, the uncertainty estimates are not particularly well-calibrated. Significance: Our study is a first step towards accurate and reliable ECG-based prediction of electrolyte concentration levels.

On Merging Feature Engineering and Deep Learning for Diagnosis, Risk-Prediction and Age Estimation Based on the 12-Lead ECG

Objective: Machine learning techniques have been used extensively for 12-lead electrocardiogram (ECG) analysis. For physiological time series, deep learning (DL) superiority to feature engineering (FE) approaches based on domain knowledge is still an open question. Moreover, it remains unclear whether combining DL with FE may improve performance. Methods: We considered three tasks intending to address these research gaps: cardiac arrhythmia diagnosis (multiclass-multilabel classification), atrial fibrillation risk prediction (binary classification), and age estimation (regression). We used an overall dataset of 2.3M 12-lead ECG recordings to train the following models for each task: i) a random forest taking the FE as input was trained as a classical machine learning approach; ii) an end-to-end DL model; and iii) a merged model of FE+DL. Results: FE yielded comparable results to DL while necessitating significantly less data for the two classification tasks and it was outperformed by DL for the regression task. For all tasks, merging FE with DL did not improve performance over DL alone. Conclusion: We found that for traditional 12-lead ECG based diagnosis tasks DL did not yield a meaningful improvement over FE, while it improved significantly the nontraditional regression task. We also found that combining FE with DL did not improve over DL alone which suggests that the FE were redundant with the features learned by DL. Significance: Our findings provides important recommendations on what machine learning strategy and data regime to chose with respect to the task at hand for the development of new machine learning models based on the 12-lead ECG.