Surprises in adversarially-trained linear regression

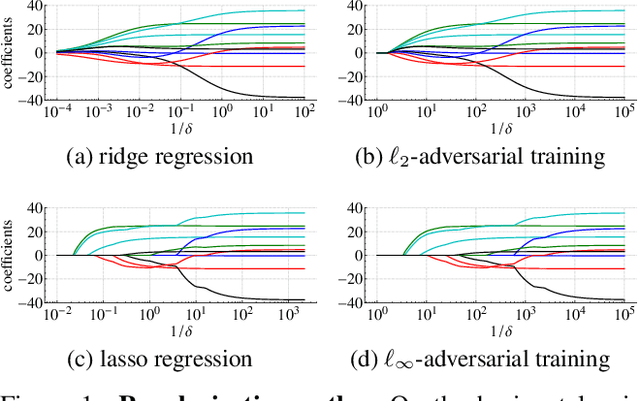
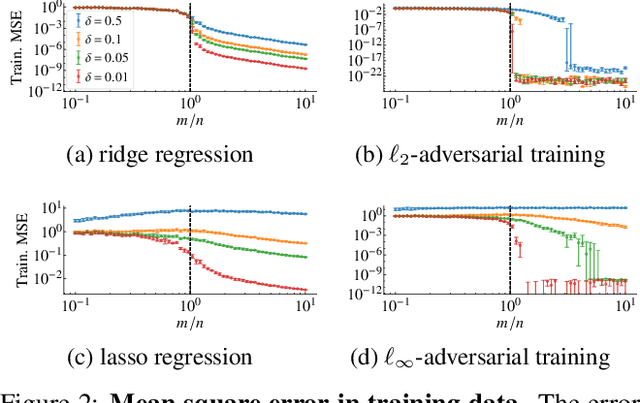
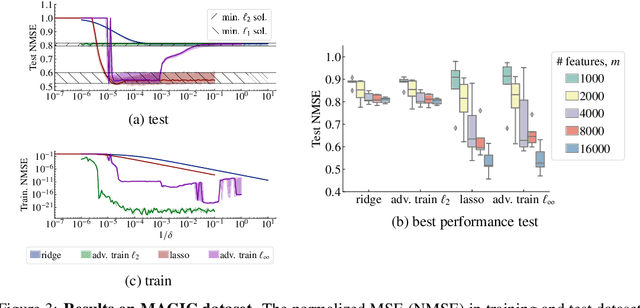
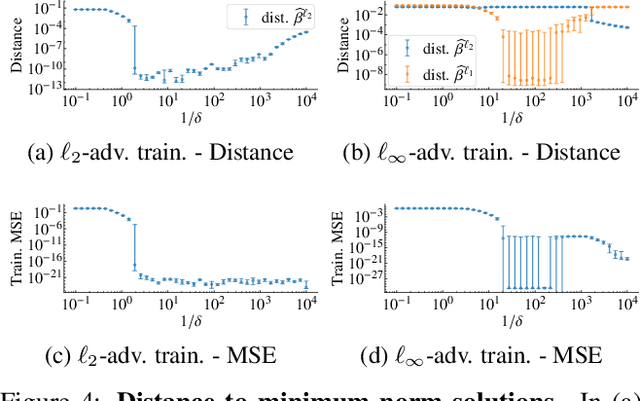
State-of-the-art machine learning models can be vulnerable to very small input perturbations that are adversarially constructed. Adversarial training is one of the most effective approaches to defend against such examples. We show that for linear regression problems, adversarial training can be formulated as a convex problem. This fact is then used to show that $\ell_\infty$-adversarial training produces sparse solutions and has many similarities to the lasso method. Similarly, $\ell_2$-adversarial training has similarities with ridge regression. We use a robust regression framework to analyze and understand these similarities and also point to some differences. Finally, we show how adversarial training behaves differently from other regularization methods when estimating overparameterized models (i.e., models with more parameters than datapoints). It minimizes a sum of three terms which regularizes the solution, but unlike lasso and ridge regression, it can sharply transition into an interpolation mode. We show that for sufficiently many features or sufficiently small regularization parameters, the learned model perfectly interpolates the training data while still exhibiting good out-of-sample performance.