Certified Inventory Control of Critical Resources

Inventory control is subject to service-level requirements, in which sufficient stock levels must be maintained despite an unknown demand. We propose a data-driven order policy that certifies any prescribed service level under minimal assumptions on the unknown demand process. The policy achieves this using any online learning method along with integral action. We further propose an inference method that is valid in finite samples. The properties and theoretical guarantees of the method are illustrated using both synthetic and real-world data.

Adaptive Parameter-Free Robust Learning using Latent Bernoulli Variables

We present an efficient parameter-free approach for statistical learning from corrupted training sets. We identify corrupted and non-corrupted samples using latent Bernoulli variables, and therefore formulate the robust learning problem as maximization of the likelihood where latent variables are marginalized out. The resulting optimization problem is solved via variational inference using an efficient Expectation-Maximization based method. The proposed approach improves over the state-of-the-art by automatically inferring the corruption level and identifying outliers, while adding minimal computational overhead. We demonstrate our robust learning method on a wide variety of machine learning tasks including online learning and deep learning where it exhibits ability to adapt to different levels of noise and attain high prediction accuracy.

Externally Valid Policy Evaluation Combining Trial and Observational Data

Randomized trials are widely considered as the gold standard for evaluating the effects of decision policies. Trial data is, however, drawn from a population which may differ from the intended target population and this raises a problem of external validity (aka. generalizability). In this paper we seek to use trial data to draw valid inferences about the outcome of a policy on the target population. Additional covariate data from the target population is used to model the sampling of individuals in the trial study. We develop a method that yields certifiably valid trial-based policy evaluations under any specified range of model miscalibrations. The method is nonparametric and the validity is assured even with finite samples. The certified policy evaluations are illustrated using both simulated and real data.

Regularization properties of adversarially-trained linear regression

State-of-the-art machine learning models can be vulnerable to very small input perturbations that are adversarially constructed. Adversarial training is an effective approach to defend against it. Formulated as a min-max problem, it searches for the best solution when the training data were corrupted by the worst-case attacks. Linear models are among the simple models where vulnerabilities can be observed and are the focus of our study. In this case, adversarial training leads to a convex optimization problem which can be formulated as the minimization of a finite sum. We provide a comparative analysis between the solution of adversarial training in linear regression and other regularization methods. Our main findings are that: (A) Adversarial training yields the minimum-norm interpolating solution in the overparameterized regime (more parameters than data), as long as the maximum disturbance radius is smaller than a threshold. And, conversely, the minimum-norm interpolator is the solution to adversarial training with a given radius. (B) Adversarial training can be equivalent to parameter shrinking methods (ridge regression and Lasso). This happens in the underparametrized region, for an appropriate choice of adversarial radius and zero-mean symmetrically distributed covariates. (C) For $\ell_\infty$-adversarial training -- as in square-root Lasso -- the choice of adversarial radius for optimal bounds does not depend on the additive noise variance. We confirm our theoretical findings with numerical examples.

Offline Policy Evaluation with Out-of-Sample Guarantees

We consider the problem of evaluating the performance of a decision policy using past observational data. The outcome of a policy is measured in terms of a loss or disutility (or negative reward) and the problem is to draw valid inferences about the out-of-sample loss of the specified policy when the past data is observed under a, possibly unknown, policy. Using a sample-splitting method, we show that it is possible to draw such inferences with finite-sample coverage guarantees that evaluate the entire loss distribution. Importantly, the method takes into account model misspecifications of the past policy -- including unmeasured confounding. The evaluation method can be used to certify the performance of a policy using observational data under an explicitly specified range of credible model assumptions.

Diagnostic Tool for Out-of-Sample Model Evaluation

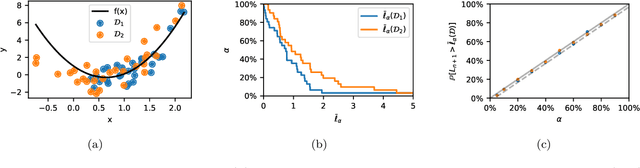
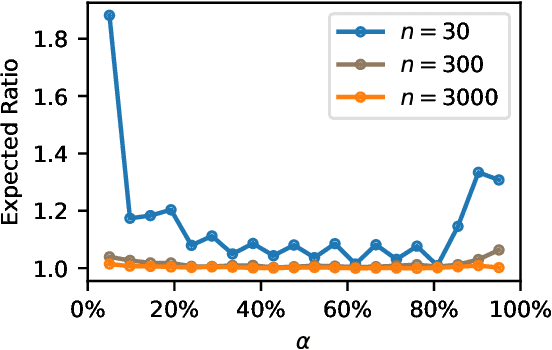
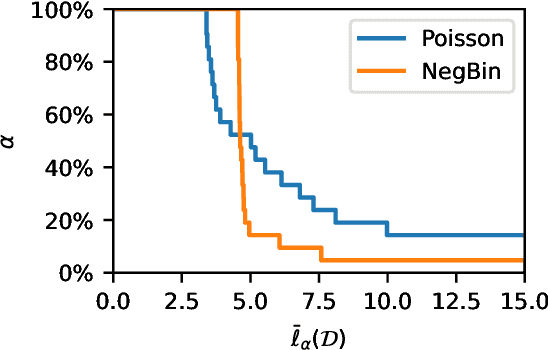
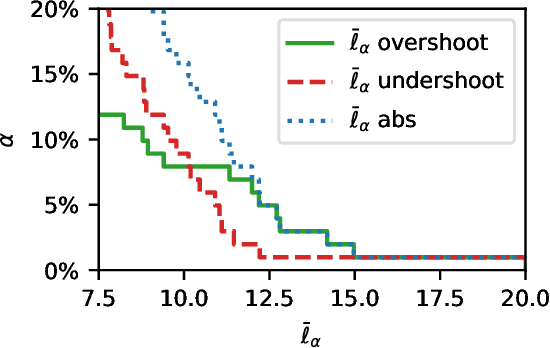
Assessment of model fitness is an important step in many problems. Models are typically fitted to training data by minimizing a loss function, such as the squared-error or negative log-likelihood, and it is natural to desire low losses on future data. This letter considers the use of a test data set to characterize the out-of-sample losses of a model. We propose a simple model diagnostic tool that provides finite-sample guarantees under weak assumptions. The tool is computationally efficient and can be interpreted as an empirical quantile. Several numerical experiments are presented to show how the proposed method quantifies the impact of distribution shifts, aids the analysis of regression, and enables model selection as well as hyper-parameter tuning.

Surprises in adversarially-trained linear regression

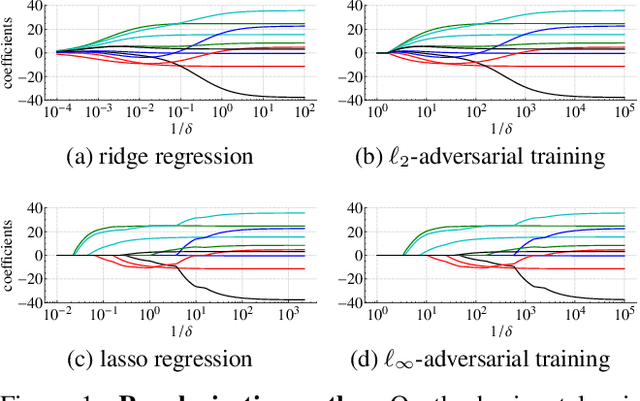
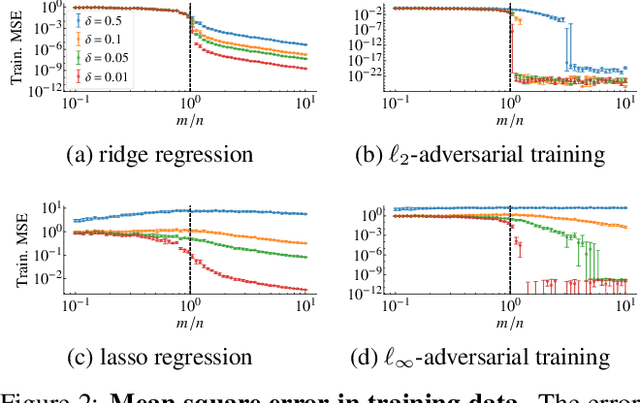
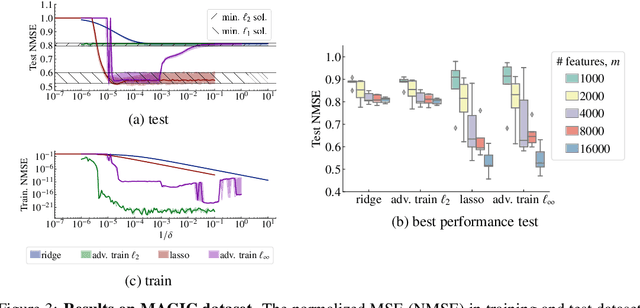
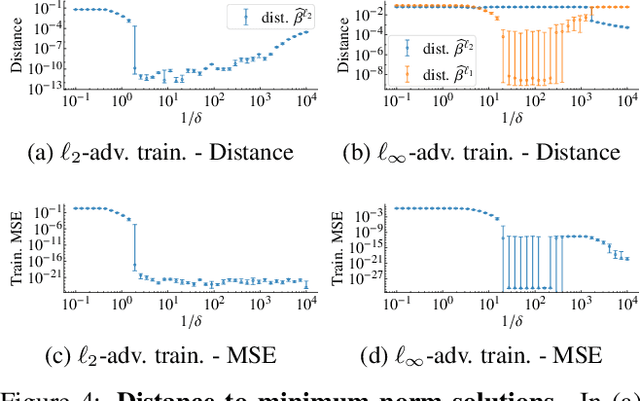
State-of-the-art machine learning models can be vulnerable to very small input perturbations that are adversarially constructed. Adversarial training is one of the most effective approaches to defend against such examples. We show that for linear regression problems, adversarial training can be formulated as a convex problem. This fact is then used to show that $\ell_\infty$-adversarial training produces sparse solutions and has many similarities to the lasso method. Similarly, $\ell_2$-adversarial training has similarities with ridge regression. We use a robust regression framework to analyze and understand these similarities and also point to some differences. Finally, we show how adversarial training behaves differently from other regularization methods when estimating overparameterized models (i.e., models with more parameters than datapoints). It minimizes a sum of three terms which regularizes the solution, but unlike lasso and ridge regression, it can sharply transition into an interpolation mode. We show that for sufficiently many features or sufficiently small regularization parameters, the learned model perfectly interpolates the training data while still exhibiting good out-of-sample performance.

Tuned Regularized Estimators for Linear Regression via Covariance Fitting

We consider the problem of finding tuned regularized parameter estimators for linear models. We start by showing that three known optimal linear estimators belong to a wider class of estimators that can be formulated as a solution to a weighted and constrained minimization problem. The optimal weights, however, are typically unknown in many applications. This begs the question, how should we choose the weights using only the data? We propose using the covariance fitting SPICE-methodology to obtain data-adaptive weights and show that the resulting class of estimators yields tuned versions of known regularized estimators - such as ridge regression, LASSO, and regularized least absolute deviation. These theoretical results unify several important estimators under a common umbrella. The resulting tuned estimators are also shown to be practically relevant by means of a number of numerical examples.

Learning Pareto-Efficient Decisions with Confidence

The paper considers the problem of multi-objective decision support when outcomes are uncertain. We extend the concept of Pareto-efficient decisions to take into account the uncertainty of decision outcomes across varying contexts. This enables quantifying trade-offs between decisions in terms of tail outcomes that are relevant in safety-critical applications. We propose a method for learning efficient decisions with statistical confidence, building on results from the conformal prediction literature. The method adapts to weak or nonexistent context covariate overlap and its statistical guarantees are evaluated using both synthetic and real data.

Distributionally Robust Learning in Heterogeneous Contexts

We consider the problem of learning from training data obtained in different contexts, where the test data is subject to distributional shifts. We develop a distributionally robust method that focuses on excess risks and achieves a more appropriate trade-off between performance and robustness than the conventional and overly conservative minimax approach. The proposed method is computationally feasible and provides statistical guarantees. We demonstrate its performance using both real and synthetic data.