Certified Inventory Control of Critical Resources

Inventory control is subject to service-level requirements, in which sufficient stock levels must be maintained despite an unknown demand. We propose a data-driven order policy that certifies any prescribed service level under minimal assumptions on the unknown demand process. The policy achieves this using any online learning method along with integral action. We further propose an inference method that is valid in finite samples. The properties and theoretical guarantees of the method are illustrated using both synthetic and real-world data.

Diagnostic Tool for Out-of-Sample Model Evaluation

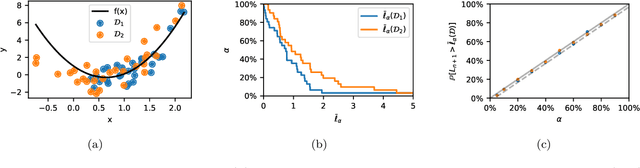
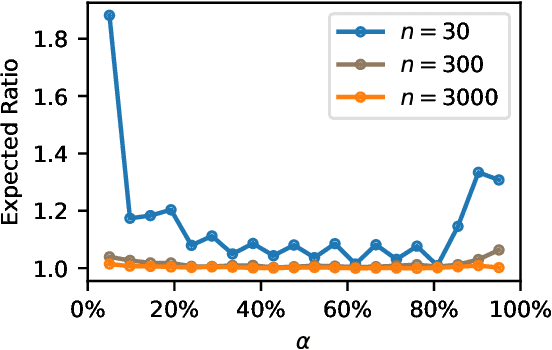
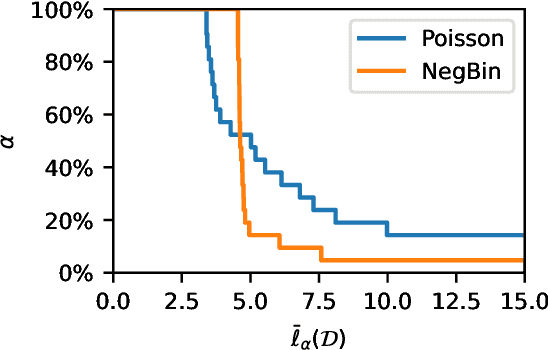
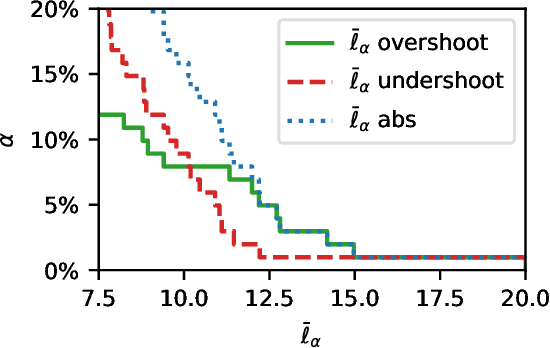
Assessment of model fitness is an important step in many problems. Models are typically fitted to training data by minimizing a loss function, such as the squared-error or negative log-likelihood, and it is natural to desire low losses on future data. This letter considers the use of a test data set to characterize the out-of-sample losses of a model. We propose a simple model diagnostic tool that provides finite-sample guarantees under weak assumptions. The tool is computationally efficient and can be interpreted as an empirical quantile. Several numerical experiments are presented to show how the proposed method quantifies the impact of distribution shifts, aids the analysis of regression, and enables model selection as well as hyper-parameter tuning.

Inference of Causal Effects when Adjustment Sets are Unknown

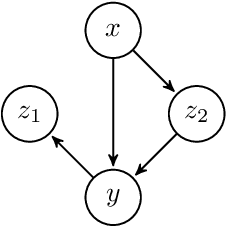
Conventional methods in causal effect inference typically rely on specifying a valid set of adjustment variables. When this set is unknown or misspecified, inferences will be erroneous. We propose a method for inferring average causal effects when the adjustment set is unknown. When the data-generating process belongs to the class of acyclical linear structural equation models, we prove that the method yields asymptotically valid confidence intervals. Our results build upon a smooth characterization of linear acyclic directed graphs. We verify the capability of the method to produce valid confidence intervals for average causal effects using synthetic data, even when the appropriate adjustment sets are unknown.